Einführung in das Programmieren für Technische Mathematik¶
C & C++¶
- Perfekt für Anwendungen in denen Performance gefragt ist
- Lehrt die inneren Vorgänge im Computer
- Erlaubt Abstraktion
Programmieren für Mathematiker¶
- Das ist keine Programmierkurs der Informatik
- Wenig Softwaredesign
- Wenig Debugging
- Wenige Algorithmen
Wichtige Infos zu EPROG¶
Info-Post im TUWEL-Forum
- Lernziele
- Regeln & Pflichten
- Benotungsschema
- Evaluation & Notenspiegel
TUWEL
- Download der Folien & Übungsblätter
- freiwilliges UE-Material (alte Tests!)
- Termine
- Zoom-Links
Literatur¶
- VO-Folien aus letzen Semestern auf TUWEL
- aktuelle Folien wöchentlich auf TUWEL
formal keine weitere Literatur nötig
mehrere Bücher zum Download auf TUWEL, z.B.
- Ralf Kirsch, Uwe Schmitt Programmieren in C, eine mathematikorientierte Einführung
- Klaus Schmaranz Softwareentwicklung in C / C++
- Online: google.com, stackoverflow.com
Programm¶
Wikipedia: Ein Computerprogramm oder kurz Programm ist eine Folge von Anweisungen, die den Regeln einer Programmiersprache genügen, um auf einem Computer eine bestimmte Funktionalität, Aufgaben- oder Problemstellung bearbeiten oder lösen zu können.
Anweisungen = Deklarationen und Instruktionen
- Deklaration = z.B. Definition von Variablen
- Instruktion = "tue etwas"
BSP: Sei
- BSP: Definiere ,
- BSP: suche einen Telefonbucheintrag
- BSP: berechne den Wert eines Integrals
Algorithmus¶
Wikipedia: Ein Algorithmus ist eine aus endlich vielen Schritten bestehende, eindeutige und ausführbare Handlungsvorschrift zur Lösung eines Problems oder einer Klasse von Problemen.
BSP: Berechne die Lösung eines linearen Gleichungssystems mittels Gauß-Elimination
BSP: Berechne die Nullstelle eines quadratischen Polynoms mittels --Formel
IdR. unendlich viele Algorithmen für ein Problem
IdR. sind Algorithmen unterschiedlich "gut"
- Was "gut" genau heißt erfahren wir später
Programmiersprachen¶
- Grobe Unterscheidung in Interpreter- und Compiler-basierte Sprachen
- Interpreter führt Source-Code zeilenweise
bei der Übersetzung aus
- d.h. Übersetzen & Ausführen ist gleichzeitig
- z.B. Matlab, Java, PHP, Python
- Compiler übersetzt Source-Code in ein
ausführbares Programm (Executable)
- Executable ist eigenständiges Programm
- d.h. (1) Übersetzen, dann (2) Ausführen
- z.B. C, C++, Fortran
- bessere Unterscheidung (siehe Schmaranz)
- imperative Sprachen, z.B. Matlab, C, Fortran
- objektorientierte, z.B. C++, Java, Python
- funktionale, z.B. Lisp
Achtung¶
- C ist Compiler-basierte Programmiersprache
Compilierter Code ist systemabhängig,
- d.h. Code läuft idR. nur auf dem System, auf dem er compiliert wurde
Source-Code ist systemunabhängig,
- d.h. er kann auch auf anderen Systemen compiliert werden.
- C-Compiler unterscheiden sich leicht
- C ist eine sehr alte Sprache (erschienen 1972)
- vielfach weiterentwickelt
- in der VO: ANSI-C = C89 (Standard von 1989)
Wie erstellt man ein C-Programm?¶
- Öffne eine (ggf. neue) Datei
name.cin einem Editor- Endung
.cist Kennung eines C-Programms
- Endung
- Schreibe den sog. Source-Code (= C-Programm)
- Source-Code abspeichern
- Compilieren z.B. mit Eingabe
gcc name.cin der Shell - Falls Code fehlerfrei, erhält man Executable
a.outunter Windows:a.exe - Diese wird durch
a.outbzw../a.outgestartet - Compilieren mit
gcc name.c -o outputerzeugt Executableoutputstatta.out
Das erste C-Programm¶
- Zeilennummern und Farben gehören nicht zum Code (sind lediglich Orientierungshilfe auf den Folien)
- Jedes C-Programm besitzt die Zeilen 3 und 6.
- Die Ausführung eines C-Programms startet immer
bei
main()- egal, womain()im Code steht - Klammern {...} schließen in C sog. Blöcke ein
1 2 3 4 5 6 | #include <stdio.h>
int main(){
printf("Hello World\n");
return 0;
}
|
Hello World
Das erste C-Programm¶
- Hauptprogramm
main()bildet immer einen Block - Logische Programmzeilen enden mit Semikolon, vgl. Zeile 4 & 5
printfgibt Text aus (in Anführungszeichen),\nmacht einen Zeilenumbruch
- Anführungszeichen müssen in derselben Zeile sein
- Zeile 1: Einbinden der Standardbibliothek für Input-Output (später mehr!)
1 2 3 4 5 6 | #include <stdio.h>
int main(){
printf("Hello World!\n");
return 0;
}
|
Hello World!
Das erste C-Programm¶
Achtung¶
- Viele Compiler erlauben das Weglassen von
intundreturn 0; - Gut zu wissen falls Sie fremden Code verwenden
1 2 3 4 5 | #include <stdio.h>
main(){
printf("Hello World!\n");
}
|
/tmp/tmpexq2n71l.c: In function ‘main’:
/tmp/tmpexq2n71l.c:6:7: error: expected ‘;’ before ‘{’ token
6 | main(){
| ^
| ;
[C kernel] GCC exited with code 1, the executable will not be executed
Fehler¶
Syntaxfehler¶
- Syntax = Wortschatz (Befehle) & Grammatik einer Sprache (Was man wie verbinden kann...)
- Syntaxfehler = Falsche Befehle oder Verwendung
- Compiler gibt Fehlermeldung
Laufzeitfehler¶
- Fehler, der erst bei Programm-Ausführung auftritt
- erst bei komplexeren Programmen möglich
- viel schwerer zu finden
- durch sorgfältiges Arbeiten möglichst vermeiden
Beispiel für Syntaxfehler¶
Der Kompiler kann die Funktion printf nicht finden, da die Bibiliothek stdio.h nicht eingebunden wurde.
1 2 3 4 | int main(){
printf("Hello World!\n");
return 0;
}
|
/tmp/tmpzwdt271q.c: In function ‘main’:
/tmp/tmpzwdt271q.c:2:5: warning: implicit declaration of function ‘printf’ [-Wimplicit-function-declaration]
2 | printf("Hello World!\n");
| ^~~~~~
/tmp/tmpzwdt271q.c:2:5: warning: incompatible implicit declaration of built-in function ‘printf’
/tmp/tmpzwdt271q.c:1:1: note: include ‘<stdio.h>’ or provide a declaration of ‘printf’
+++ |+#include <stdio.h>
1 | int main(){
Hello World!
Beispiel für Syntaxfehler¶
Der Kompiler beschwert sich über das fehlende Semikolon ; in Zeile 4.
1 2 3 4 5 6 | #include <stdio.h>
int main(){
printf("Hello World!\n")
return 0;
}
|
Hello World!
Die ersten Sprachelemente¶
Variablen¶
- Variable = symbolischer Name für Speicherbereich
- Variable in Math. und Informatik verschieden:
- Mathematik: Sei fixiert
- Informatik:
x = 5weist x den Wert zu, Zuweisung kann jederzeit geändert werden z.B.x = 7
Variablen-Namen¶
bestehen aus Zeichen, Ziffern und Underscore _
- maximale Länge = 31
- erstes Zeichen darf keine Ziffer sein
Klein- und Großschreibung wird unterschieden
- d.h. Var, var, VAR sind 3 verschiedene Variablen
- Konvention: Namen sind
klein_mit_underscores
Datentypen¶
Bevor man Variable benutzen darf, muss man idR. erklären, welchen Typ Variable haben soll
Elementare Datentypen:
- Gleitkommazahlen (ersetzt , ), z.B.
double - Integer, Ganzzahlen (ersetzt , ), z.B.
int - Zeichen (Buchstaben)
char
- Gleitkommazahlen (ersetzt , ), z.B.
int x;deklariert Variablexvom Typint
Deklaration¶
- Deklaration = das Anlegen einer Variable
- d.h. Zuweisung von Speicherbereich auf einen
symbolischen Namen & Angabe des Datentyps
- Zeile
int x;deklariert Variablexvom Typint - Zeile
double var;deklariertvarvom Typdouble
- Zeile
- d.h. Zuweisung von Speicherbereich auf einen
symbolischen Namen & Angabe des Datentyps
1 2 | int x;
double var;
|
Initialisierung¶
- Durch Deklaration einer Variablen wird lediglich Speicherbereich zugewiesen
- Falls noch kein konkreter Wert zugewiesen:
- Wert einer Variable ist zufällig
- Deshalb direkt nach Deklaration der neuen
Variable Wert zuweisen, sog. Initialisierung
int x;(Deklaration)x = 0;(Initialisierung)
- Deklaration & Initialisierung auch in einer Zeile
möglich:
int x = 0;
1 2 | int x = 0;
double var=3.1415;
|
Einbinden der Input-Output-Funktionen (Zeile 1)
printfgibt Text (oder Wert einer Var.) ausscanfliest Tastatureingabe ein in eine Variable
Prozentzeichen
%in Zeile 7/8 leitet Platzhalter ein
1 2 3 4 5 6 7 8 9 | #include <stdio.h>
int main() {
int x = 0;
printf("Input: x=");
scanf("%d",&x);
printf("Output: x=%d\n",x);
}
|
Input: x=4 Output: x=4, 12
Es gibt verschiedene Platzhalter für verschiedene Datentypen.
| Datentyp | Platzhalter printf |
Platzhalter scanf |
|---|---|---|
int |
%d |
%d |
double |
%f |
%lf |
char |
%c |
%c |
1 2 3 4 5 6 7 8 9 | #include <stdio.h>
int main() {
double x = 0;
printf("Input: x=");
scanf("%lf",&x);
printf("Output: x=%f\n",x);
}
|
Input: x=3.1234 Output: x=3.123400
Beachte
&beiscanfin Zeile 7scanf("%d", & x)- aber:
printf("%d", x)
Wenn man
&vergisst Laufzeitfehler- Compiler merkt Fehler nicht (kein Syntaxfehler!)
- Sorgfältig arbeiten!
1 2 3 4 5 6 7 8 9 | #include <stdio.h>
int main() {
int x = 0;
printf("Input: x=");
scanf("%d",x);
printf("Output: x=%d\n",x);
}
|
Input: x=3
[C kernel] Executable exited with code -11
Achtung bei double nicht %lf vergessen!
1 2 3 4 5 6 7 8 9 | #include <stdio.h>
int main() {
double x = 0;
printf("Input: x=");
scanf("%f",&x);
printf("Output: x=%f\n",x);
}
|
Input: x=3.1415 Output: x=3.141500
Zuweisungsoperator =¶
Das einfache Gleich
=ist Zuweisungsoperator- Zuweisung immer rechts nach links!
Zeile
x = 1;weist den Wert auf der rechten Seite der VariablenxzuZeile
x = y;weist den Wert der Variablenyder Variablenxzu- insb. haben
xundydanach denselben Wert - d.h. Vertauschen der Werte nur mit Hilfsvariable
- insb. haben
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | #include <stdio.h>
int main() {
int x = 1;
int y = 2;
int tmp = 0;
printf("a) x=%d, y=%d, tmp=%d\n",x,y,tmp);
tmp = x;
x = y;
y = tmp;
printf("b) x=%d, y=%d, tmp=%d\n",x,y,tmp);
}
|
a) x=1, y=2, tmp=0 b) x=2, y=1, tmp=1
Arithmetische Operatoren¶
Bedeutung eines Operators kann vom Datentyp abhängen!
Operatoren auf Ganzzahlen:
a=b,-a(Vorzeichen)a+b,a-b,a*b,a/b(Division ohne Rest),a%b(Divisionsrest)a+=betc. gleichbedeutend mita=a+b
Operatoren auf Gleitkommazahlen:
a=b,-a(Vorzeichen)a+b,a-b,a*b,a/b("normale" Division)a+=betc. gleichbedeutend mita=a+b
Arithmetische Operatoren¶
Achtung:
2/3ist Ganzzahl-Division, also Null!Notation für Gleitkommazahlen:
- Vorzeichen
-, falls negativ - Vorkommastellen
- Dezimalpunkt
- Nachkommastellen
eoderEmit ganzzahligem Exponenten (10er Potenz!), z.B.- Wegfallen darf entweder Vor- oder Nach- kommastelle (sonst sinnlos, da kein Wert!)
- Wegfallen darf entweder Dezimalpunkt oder
ebzw.Emit Exponent (sonst wird die Zahl als Integer verstanden, vgl.2/3)
- Vorzeichen
Also:
2./3.ist Gleitkommadivision (beidoubleca. auf 16 Stellen genau)
Type Casting¶
- Operatoren können auch Variablen verschiedener Datentypen verbinden
Vor der Ausführung werden beide Variablen auf denselben Datentyp gebracht (Type Casting)
Welchen Datentyp hat
x+yin Zeile 7, 8?- Den mächtigeren Datentyp, also
double! - so wie , so ist
doublemächtiger alsint - Type Casting von Wert
xaufdouble
- Den mächtigeren Datentyp, also
- Zeile 7: Type Casting, da
doubleaufintZuweisung- durch Abschneiden, nicht durch Rundung!
1 2 3 4 5 6 7 8 9 10 11 12 | #include <stdio.h>
int main() {
int x = 1;
double y = 2.8;
int sum_int = x+y;
double sum_dbl = x+y;
printf("sum_int = %d\n",sum_int);
printf("sum_dbl = %f\n",sum_dbl);
}
|
sum_int = 3 sum_dbl = 3.800000
Implizites Typecasting¶
Warum Ergebnis in a) und d) ?
2,3sindint2/3ist Ganzzahl-Division- Werden Variablen verschiedenen Typs durch arith. Operator verbunden, Type Casting auf "gemeinsamen" (mächtigeren) Datentyp
- vgl. Zeile 5, 13, 14
2istint,3.istdouble2/3.ergibtdouble
- Der C-Compiler setzt die kanonischen Regeln um:
- Punkt-Rechnung vor Strich-Rechnung
- gleichwertige Operatoren von links nach rechts
- vgl. Zeile 13, 14
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #include <stdio.h>
int main() {
double dbl1 = 2 / 3;
double dbl2 = 2 / 3.;
double dbl3 = 1E2;
int int1 = 2;
int int2 = 3;
printf("a) %f\n",dbl1);
printf("b) %f\n",dbl2);
printf("c) %f\n",dbl3 * int1 / int2);
printf("d) %f\n",dbl3 * (int1 / int2) );
}
|
a) 0.000000 b) 0.666667 c) 66.666667 d) 0.000000
Explizites Type Casting¶
- Kann dem Compiler mitteilen, in welcher Form eine Variable interpretiert
werden muss
- Dazu Ziel-Typ in Klammern voranstellen!
- In Zeile 7, 8, 9: Explizites Type Casting
(jeweils von
intzudouble) - In Zeile 6, 8, 9: Implizites Type Casting
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #include <stdio.h>
int main() {
int a = 2;
int b = 3;
double dbl1 = a / b;
double dbl2 = (double) (a / b);
double dbl3 = (double) a / b;
double dbl4 = a / (double) b;
printf("a) %f\n",dbl1);
printf("b) %f\n",dbl2);
printf("c) %f\n",dbl3);
printf("d) %f\n",dbl4);
}
|
a) 0.000000 b) 0.000000 c) 0.666667 d) 0.666667
Fehlerquelle beim Type Casting¶
- Implizites Type Casting sollte man vermeiden!
- d.h. Explizites Type Casting verwenden!
- Bei Rechnungen Zwischenergebnisse in richtigen Typen speichern!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <stdio.h>
int main() {
int a = 2;
int b = 3;
double dbl = (double) a / b;
int i = dbl;
printf("a) %f\n",dbl);
printf("b) %f\n",dbl*b);
printf("c) %d\n",i);
printf("d) %d\n",i*b);
}
|
a) 0.666667 b) 2.000000 c) 0 d) 0
Einfache Verzweigung¶
Logische Operatoren¶
- Es seien
a,bzwei Variablen (auch versch. Typs!)- Vergleich (z.B.
a < b) liefert Wert1, falls wahr, bzw.0, falls falsch
- Vergleich (z.B.
Übersicht über Vergleichsoperatoren:
Symbol Bedeutung ==Gleichheit (ACHTUNG mit Zuweisung!) !=Ungleichheit >echt größer <echt kleiner >=größer oder gleich <=kleiner oder gleich Bei Vergleichen stets Klammern setzen (häufig unnötig aber oft besser lesbar)
Weitere logische Operatoren
| Symbol | Bedeutung |
|---|---|
! |
Nicht |
&& |
und |
|| |
oder |
Logische Verkettung¶
- Warum ist Aussage in Zeile 10 falsch, aber in Zeile 13 wahr?
- Auswertung von links nach rechts:
a > bist wahr, also mit1bewertet1 > cist falsch, also mit0bewertet- Also wird
a > b > cmit falsch bewertet! - Aussage in 10 ist also nicht korrekt formuliert!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #include <stdio.h>
int main() {
int result = 0;
int a = 3;
int b = 2;
int c = 1;
result = (a > b > c);
printf("a) result=%d\n",result);
result = (a > b) && (b > c);
printf("b) result=%d\n",result);
}
|
/tmp/tmpl7rt034j.c: In function ‘main’:
/tmp/tmpl7rt034j.c:10:15: warning: comparisons like ‘X<=Y<=Z’ do not have their mathematical meaning [-Wparentheses]
10 | result = (a > b > c);
| ~~^~~
a) result=0 b) result=1
if-else¶
- einfache Verzweigung: Wenn - Dann - Sonst
if (condition)statementAelsestatementB- nach
ifsteht Bedingung stets in runden Klammern - nach Bedingung steht nie Semikolon
- Bedingung ist falsch, falls sie ist bzw. mit bewertet
wird, sonst ist die Bedingung wahr
- Bedingung wahr statementA wird ausgeführt
- Bedingung falsch statementB wird ausgeführt
- Statement ist
- entweder eine Zeile (d.h. bis zum Semikolon!)
- oder mehrere Zeilen in geschwungenen
Klammern
{ ... }, sog. Block
else-Zweig ist optional- d.h.
else statementBdarf entfallen
- d.h.
Beispiel zu if¶
- abhängige Zeilen einrücken (Lesbarkeit!)
- WARNUNG: Nicht-Verwendung von Blöcken
{...}ist fehleranfällig (Zeile 9--10)- besser: Block (analog zu Zeile 12--14)
- könnte zusätzlich
elsein Zeile 11 schreiben- da
if's sich ausschließen
- da
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #include <stdio.h>
int main() {
int x = 0;
printf("Input x=");
scanf("%d",&x);
if (x < 0)
printf("x=%d is negative\n",x);
if (x > 0) {
printf("x=%d is positive\n",x);
}
}
|
Input x=3 x=3 is positive
Beispiel zu if-else¶
- Eine Bedingung ist wahr, falls Wert
- z.B. Zeile 15, aber besser:
if ( var2!= 0)
- z.B. Zeile 15, aber besser:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | #include <stdio.h>
int main() {
int var1 = -5;
double var2 = 1e-32;
int var3 = 5;
if (var1 >= 0) {
printf("var1 >= 0\n");
}
else {
printf("var1 < 0\n");
}
if (var2) {
printf("var2 != 0, i.e., cond. is true\n");
}
else {
printf("var2 == 0, i.e., cond. is false\n");
}
if ( (var1 < var2) && (var2 < var3) ) {
printf("var2 lies between the others\n");
}
}
|
var1 < 0 var2 != 0, i.e., cond. is true var2 lies between the others
Gerade oder Ungerade?¶
- Programm überprüft, ob eingegebene Zahl x gerade Zahl ist oder nicht
- Man kann Verzweigungen schachteln:
- Einrückungen machen Code übersichtlicher
- formal nicht notwendig, aber trotzdem!
- Abhängigkeiten werden verdeutlicht
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <stdio.h>
int main() {
int x = 0;
printf("Input x=");
scanf("%d",&x);
if (x > 0) {
if (x%2 != 0) {
printf("x=%d is odd\n",x);
}
else {
printf("x=%d is even\n",x);
}
}
else {
printf("Error: Input has to be positive!\n");
}
}
|
Input x=3 x=3 is odd
Zwei Zahlen aufsteigend sortieren¶
- Eingabe von zwei Zahlen Zahlen werden aufsteigend sortiert
- ggf. vertauscht
- Ergebnis wird ausgegeben
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | #include <stdio.h>
int main() {
double x1 = 0;
double x2 = 0;
double tmp = 0;
printf("Unsorted input:\n");
printf(" x1=");
scanf("%lf",&x1);
printf(" x2=");
scanf("%lf",&x2);
if (x1 > x2) {
tmp = x1;
x1 = x2;
x2 = tmp;
}
printf("Sorted output (ascending order):\n");
printf(" x1=%f\n",x1);
printf(" x2=%f\n",x2);
}
|
Unsorted input: x1=3 x2=1 Sorted output (ascending order): x1=1.000000 x2=3.000000
Innen oder Außen?¶
- liegt im Kreis um mit Radius , falls
- auf Kreisrand, falls
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | #include <stdio.h>
int main() {
double r = 0;
double x1 = 0;
double x2 = 0;
double z1 = 0;
double z2 = 0;
double dist2 = 0;
printf("Radius of the circle: r=");
scanf("%lf",&r);
printf("Center of the circle: x = (x1,x2)\n");
printf(" x1=");
scanf("%lf",&x1);
printf(" x2=");
scanf("%lf",&x2);
printf("Point in the plane: z = (z1,z2)\n");
printf(" z1=");
scanf("%lf",&z1);
printf(" z2=");
scanf("%lf",&z2);
dist2 = (x1-z1)*(x1-z1) + (x2-z2)*(x2-z2);
if ( dist2 < r*r ) {
printf("z is inside the circle\n");
}
else {
if ( dist2 > r*r ) {
printf("z is outside of the circle\n");
}
else {
printf("z lies on the boundary of the circle\n");
}
}
}
|
Radius of the circle: r=3 Center of the circle: x = (x1,x2) x1=0 x2=0 Point in the plane: z = (z1,z2) z1=1 z2=2 z is inside the circle
Gleichheit vs. Zuweisung¶
- Nur Erinnerung:
if (a==b)vs.if (a=b)- beides ist syntaktisch korrekt!
if (a==b)ist Abfrage auf Gleichheit- ist vermutlich so gewollt...
- ABER:
if (a=b)- weist
aden Wert vonbzu - dann Abfrage, ob
- weist
- Letzteres ist schlechter Programmierstil!
- da zwei Aktionen in einer Programmzeile
Strukturierung mit Blöcken¶
Lifetime & Scope¶
Lifetime einer Variable = Zeitraum, in dem Speicherplatz zugewiesen ist = Zeitraum, in dem Variable existiert
Scope einer Variable = Zeitraum, in dem Variable sichtbar ist = Zeitraum, in dem Variable gelesen/verändert werden kann
Scope Lifetime
Globale & Lokale Variablen¶
globale Variablen = Variablen, die globale Lifetime haben (bis Programm terminiert)
- eventuell lokaler Scope
- werden am Anfang außerhalb von main deklariert
lokale Variablen = Variablen, die nur lokale Lifetime haben
- Konvention: erkenne Variable am Namen
- lokale Variablen sind
klein_mit_underscores - globale Var. haben
auch_underscore_hinten_
- lokale Variablen sind
Blöcke¶
Blöcke stehen innerhalb von
{...}Jeder Block startet mit Deklaration zusätzlich benötigter Variablen
- Variablen sollten nur am Anfang eines Blocks deklariert werden
Die innerhalb des Blocks deklarierten Variablen werden nach Blockende vergessen (= gelöscht)
- d.h. Lifetime endet
- lokale Variablen
Schachtelung
{..{..}..}- beliebige Schachtelung ist möglich
- Variablen aus äußerem Block können im inneren Block gelesen und verändert werden, umgekehrt nicht. Änderungen bleiben wirksam.
- d.h. Lifetime & Scope nur nach Innen vererbt
- Wird im äußeren und im inneren Block Variable
vardeklariert, so wird das "äußere"varüberdeckt und ist erst wieder ansprechbar (mit gleichem Wert wie vorher), wenn der innere Block beendet wird.- d.h. äußeres
varist nicht im inneren Scope - Das ist schlechter Programmierstil!
- siehe die Beispiele auf den nächsten 2 Folien!
- d.h. äußeres
Einfaches Beispiel¶
- zwei verschiedene lokale Variablen
x- Deklaration + Initialisierung (Zeile 4, 9)
- unterscheide von Zuweisung (Zeile 6)
1 2 3 4 5 6 7 8 9 10 11 12 13 | #include <stdio.h>
int main() {
int x = 7;
printf("a) %d\n", x);
x = 9;
printf("b) %d\n", x);
{
int x = 17;
printf("c) %d\n", x);
}
printf("d) %d\n", x);
}
|
a) 7 b) 9 c) 17 d) 9
Komplizierteres Beispiel¶
- zwei Variablen mit Name
var0(Zeile 3 + 18)- Namenskonvention absichtlich verletzt
- zwei Variablen mit Name
var1(Zeile 6 + 11)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | #include <stdio.h>
int var0 = 5;
int main() {
int var1 = 7;
int var2 = 9;
printf("a) %d, %d, %d\n", var0, var1, var2);
{
int var1 = 17;
printf("b) %d, %d, %d\n", var0, var1, var2);
var0 = 15;
var2 = 19;
printf("c) %d, %d, %d\n", var0, var1, var2);
{
int var0 = 25;
printf("d) %d, %d, %d\n", var0, var1, var2);
}
}
printf("e) %d, %d, %d\n", var0, var1, var2);
}
|
a) 5, 7, 9 b) 5, 17, 9 c) 15, 17, 19 d) 25, 17, 19 e) 15, 7, 19
Funktionen¶
Beispiel: Quadrieren¶
Compiler muss Funktion vor Aufruf kennen
- d.h. Funktion vor aufrufender Zeile definieren
Ausführung startet immer bei
main()Die Variable
xin Funktionsquare()und die Variablexin Funktionmain()sind verschieden!
1 2 3 4 5 6 7 8 9 10 11 12 | #include <stdio.h>
double square(double x) {
return x*x;
}
int main() {
double x = 0;
printf("Input x = ");
scanf("%lf",&x);
printf("%f^2 = %f\n",x,square(x));
}
|
Input x = 3 3.000000^2 = 9.000000
Funktionen¶
Funktion = Zusammenfassung mehrerer Anweisungen zu einem aufrufbaren Ganzen
output = function(input)- Eingabeparameter
input - Ausgabeparameter (Return Value)
output
Warum Funktionen?
- Zerlegung eines großen Problems in überschaubare kleine Teilprobleme
- Strukturierung von Programmen (Abstraktionsebenen)
- Wiederverwertung von Programm-Code
Funktion besteht aus Signatur und Rumpf (Body)
- Signatur = Funktionsname & Eingabe-Ausgabeparameter
- Anzahl & Reihenfolge ist wichtig!
- Rumpf = Programmzeilen der Funktion
Namenskonvention¶
- lokale Variablen sind
klein_mit_underscores - globale Var. haben
auch_underscore_hinten_ - Funktionen sind
erstesWortKleinKeineUnderscores
Funktionen in C¶
In C können Funktionen
- mehrere (oder keinen) Parameter übernehmen
- einen einzigen oder keinen Rückgabewert liefern
- Rückgabewert muss elementarer Datentyp sein
- z.B.
double,int
Signatur hat folgenden Aufbau
<type of return value> <function name>(parameters)- Funktion ohne Rückgabewert:
<type of return value>=void- Sonst:
<type of return value>= Variablentyp parameters= Liste der Übergabeparameter- getrennt durch Kommata
- vor jedem Parameter Variablentyp angeben
- kein Parameter leere Klammer
()
Funktionen in C¶
- Rumpf ist ein Block
- Rücksprung ins Hauptprogramm mit
returnoder bei Erreichen des Funktionsblock-Endes, falls Funktionstyp =void - Rücksprung ins Hauptprogramm mit
- Rücksprung ins Hauptprogramm mit
return output, falls die Variableoutputzurückgegeben werden soll- Häufiger Fehler: return vergessen
- Dann Rückgabewert zufällig!
- Irgendwann Chaos (Laufzeitfehler!)
Variablen¶
Alle Variablen, die im Funktionsblock deklariert werden, sind lokale Variablen
Alle elementaren Variablen, die in Signatur deklariert werden, sind lokale Variablen
Funktion bekommt Input-Parameter als Werte, ggf. Type Casting!
Call by Value¶
- Dass bei Funktionsaufrufen Input-Parameter in
lokale Variablen kopiert werden, bezeichnet man
als Call by Value
- Es wird neuer Speicher angelegt, der Wert der Eingabe-Parameter wird in diese kopiert
Beispiel: Minimum zweier Zahlen¶
- Programm erfüllt Aufgabenstellung der UE:
- Funktion mit gewisser Funktionalität
- aufrufendes Hauptprogramm mit
- Daten einlesen
- Funktion aufrufen
- Ergebnis ausgeben
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | #include <stdio.h>
double min(double x, double y) {
if (x > y) {
return y;
}
else {
return x;
}
}
int main() {
double x = 0;
double y = 0;
printf("Input x = ");
scanf("%lf",&x);
printf("Input y = ");
scanf("%lf",&y);
printf("min(x,y) = %f\n",min(x,y));
}
|
Input x = 3 Input y = 4 min(x,y) = 3.000000
Deklaration von Funktionen¶
Bei vielen Funktionen wird Code unübersichtlich
- Alle Funktionen oben deklarieren, vgl. Zeile 3
- Compiler weiß dann, wie Funktion agiert
- vollständiger Fkt.code folgt, vgl. Zeile 16-23
Alternative Deklaration = Fkt.code ohne Rumpf
double min(double x, double y);vgl. Zeile 3, 16
in Literatur: Forward Declaration und Prototyp
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | #include <stdio.h>
double min(double, double);
int main() {
double x = 0;
double y = 0;
printf("Input x = ");
scanf("%lf",&x);
printf("Input y = ");
scanf("%lf",&y);
printf("min(x,y) = %f\n",min(x,y));
}
double min(double x, double y) {
if (x > y) {
return y;
}
else {
return x;
}
}
|
Input x = 3 Input y = 4 min(x,y) = 3.000000
Beispiel zu Call by Value¶
- Die Funktionsparameter werden auf lokale Variablen kopiert
- Später werden wir auch "Call by Reference" kennenlernen
- da wird tatsächlich die Variable selbst (oder eine Referenz auf die Variable) übergeben
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <stdio.h>
void test(int x) {
printf("a) x=%d\n", x);
x = 43;
printf("b) x=%d\n", x);
}
int main() {
int x = 12;
printf("c) x=%d\n", x);
test(x);
printf("d) x=%d\n", x);
}
|
c) x=12 a) x=12 b) x=43 d) x=12
Type Casting & Call by Value¶
- Type Casting von
intaufdoublebei Übergabe
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #include <stdio.h>
double divide(double, double);
int main() {
int int1 = 2;
int int2 = 3;
printf("a) %f\n", int1 / int2 );
printf("b) %f\n", divide(int1,int2));
}
double divide(double dbl1, double dbl2) {
return(dbl1 / dbl2);
}
|
a) 0.000000 b) 0.666667
Type Casting (Negativbeispiel!)¶
- Eigentlich !
- Implizites Type Casting von
doubleaufintdurch Abschneiden, denn Input-Parameter sindint
- Implizites Type Casting von
- Achtung mit Type Casting bei Funktionen!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | #include <stdio.h>
int isEqual(int, int);
int main() {
double x = 4.1;
double y = 4.9;
if (isEqual(x,y)) {
printf("x == y\n");
}
else {
printf("x != y\n");
}
}
int isEqual(int x, int y) {
if (x == y) {
return 1;
}
else {
return 0;
}
}
|
x == y
Kommentare im Code¶
Kommentarzeilen¶
- werden vom Interpreter/Compiler ausgelassen
- nur für den Leser des Programmcodes
- notwendig, um eigene Programme auch später
noch zu begreifen
- deshalb brauchbar für Übung!
- notwendig, damit andere den Code verstehen
- soziale Komponente der Übung?
extrem brauchbar zum debuggen
- Teile des Source-Code "auskommentieren", sehen was passiert...
- vor allem bei Fehlermeldungen des Parser
Wichtige Regeln:
- nie dt. Sonderzeichen verwenden
- nicht zu viel und nicht zu wenig
- jetzt am Anfang mehr, später weniger!
- bei großen Projekten mit mehreren AutorInnen Name & letzte Änderung kommentieren
- vermeidet das Arbeiten an alten Versionen...
Kommentarzeilen in C¶
Gibt in C zwei Typen von Kommentaren:
- einzeiliger Kommentar
- eingeleitet durch
//, geht bis Zeilen ende - z.B. Zeile 4
- stammt eigentlich aus C++
- eingeleitet durch
- mehrzeiliger Kommentar
- alles zwischen
/*(Anfang) und*/(Ende) - z.B. Zeile 6--9
- darf nicht geschachtelt werden!
- d.h.
/* ... /* ... */ ... */ist Syntaxfehler
- alles zwischen
- einzeiliger Kommentar
Vorschlag
- Verwende
//für echte Kommentare - Verwende
/*...*/zum Debuggen
- Verwende
1 2 3 4 5 6 7 8 9 10 11 12 | #include <stdio.h>
int main() {
// printf("1 ");
printf("2 ");
/*
printf("3");
printf("4");
*/
printf("5");
printf("\n");
}
|
2 5
Beispiel zu vernünftigem Kommentieren von Code¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | // Exercise 0.1 -- how to comment a program
// author: Michael Feischl
// last modified: 11.03.2020
#include <stdio.h>
double min(double, double);
int main() {
double x = 0;
double y = 0;
// read input x
printf("Input x = ");
scanf("%lf",&x);
// read input y
printf("Input y = ");
scanf("%lf",&y);
// determine and print minimum
printf("min(x,y) = %f\n",min(x,y));
}
// The function min determines the mininum of two
// double values x and y
double min(double x, double y) {
if (x > y) {
// if x > y, then min(x,y) = y
return y;
}
else {
// otherwise, x <= y and min(x,y) = x
return x;
}
}
|
Input x = 3 Input y = 4 min(x,y) = 3.000000
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | // author: Dirk Praetorius
// last modified: 15.03.2020
#include <stdio.h>
// The Euclidean algorithm to compute the greatest
// common divisor (gcd) is based on gcd(a,b) = gcd(a-b,b)
// for a>b and gcd(a,b) = gcd(b,a).
int euclid(int a, int b) {
int tmp = 0;
// iteration gcd(a,b) = gcd(a-b,b), realized
// using division with remainder, until b = 0.
// Then, since it was a==b, it holds gcd = a.
while (b != 0) {
tmp = a%b;
a = b;
b = tmp;
}
return a;
}
int main(){
int a = 200;
int b = 110;
printf("gcd(%d,%d)=%d\n",a,b,euclid(a,b));
}
|
gcd(200,110)=10
Rekursionen¶
Rekursive Funktion¶
- Funktion ist rekursiv, wenn sie sich selber aufruft
- natürliches Konzept in der Mathematik:
- d.h. Rückführung eines Problems auf einfacheres Problem derselben Art
- Achtung:
- Rekursion darf nicht endlos sein
- d.h. Abbruchbedingung für Rekursion ist wichtig
- häufig Schleifen statt Rekursion möglich (später!)
- idR. Rekursion eleganter
- idR. Schleifen effizienter
Beispiel: Faktorielle¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | #include <stdio.h>
// The function factorial computes the factorial
// of a nonnegative integer n recursively
int factorial(int n) {
if (n <= -1) {
// factorial not defined for n <= -1
return -1;
}
else {
if (n > 1) {
// recursive step n! = n*(n-1)!
return n*factorial(n-1);
}
else {
// stopping criterion 0! = 1 = 1!
return 1;
}
}
}
int main() {
int n = 0;
int nfac = 0;
printf("n=");
scanf("%d",&n);
nfac = factorial(n);
if (nfac <= 0) {
printf("Wrong input!\n");
}
else {
printf("%d!=%d\n",n,nfac);
}
}
|
n=5 5!=120
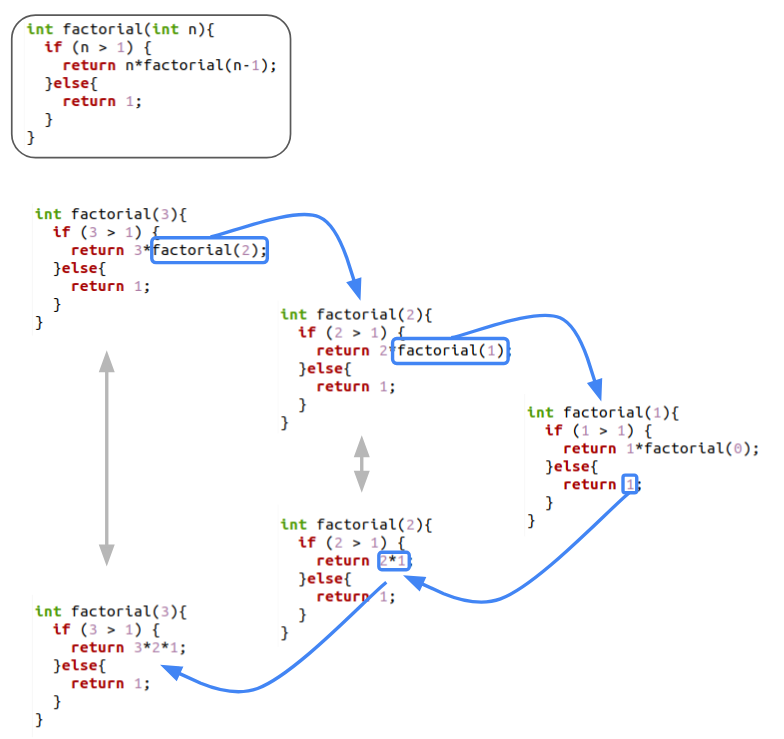
Reihenfolge der Selbstaufrufe am Beispiel Faktorielle¶
- Die blauen Pfeile symbolisieren die Funktionsaufrufe (oben) und die Rückgaben (unten).
- Die grauen Pfeile verdeutlichen, dass es sich oben und unten um die selbe Funktion handelt, aber der Selbstaufruf durch den Rückgabewert ersetzt wird.
Nullstellensuche mit dem Bisektionsverfahren¶
Gegeben: stetiges mit
- Toleranz
Tatsache: Zwischenwertsatz mind. eine Nst
- denn und haben versch. Vorzeichen
Gesucht: mit folgender Eigenschaft
- und
Bisektionsverfahren = iterierte Intervallhalbierung
- Solange wie Intervallbreite
- Berechne Intervallmittelpunkt und
- Falls , betrachte Intervall
- sonst betrachte halbiertes Intervall
- ist schließlich gesuchte Approximation
- Verfahren basiert nur auf Zwischenwertsatz
Terminiert nach endlich vielen Schritten, da jeweils Intervall halbiert wird
Konvergenz gegen Nst. für .
Illustration des Bisektionsverfahrens¶
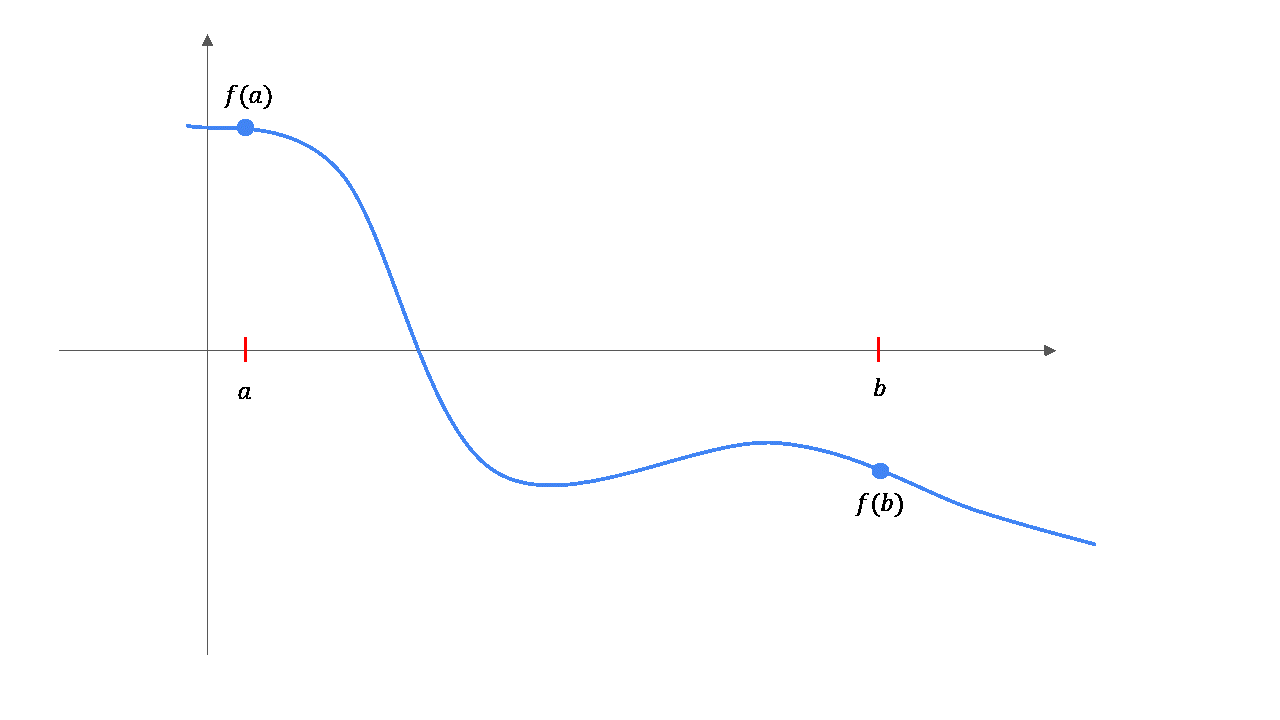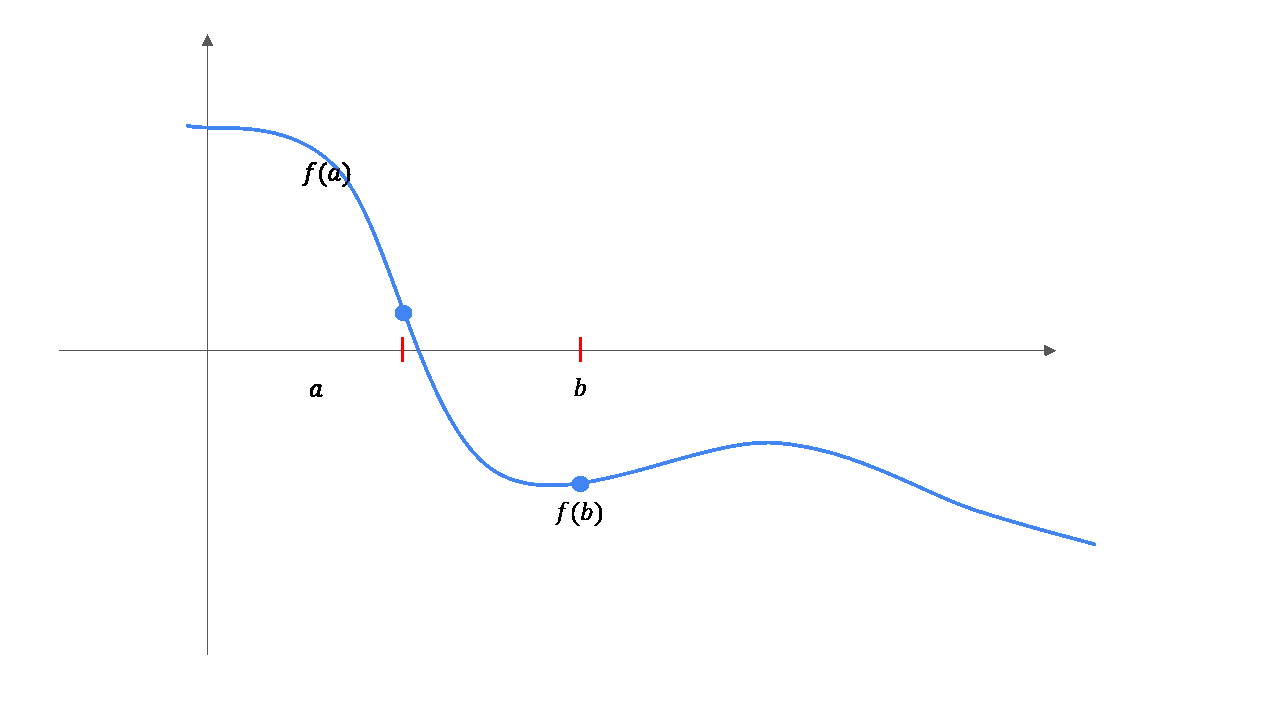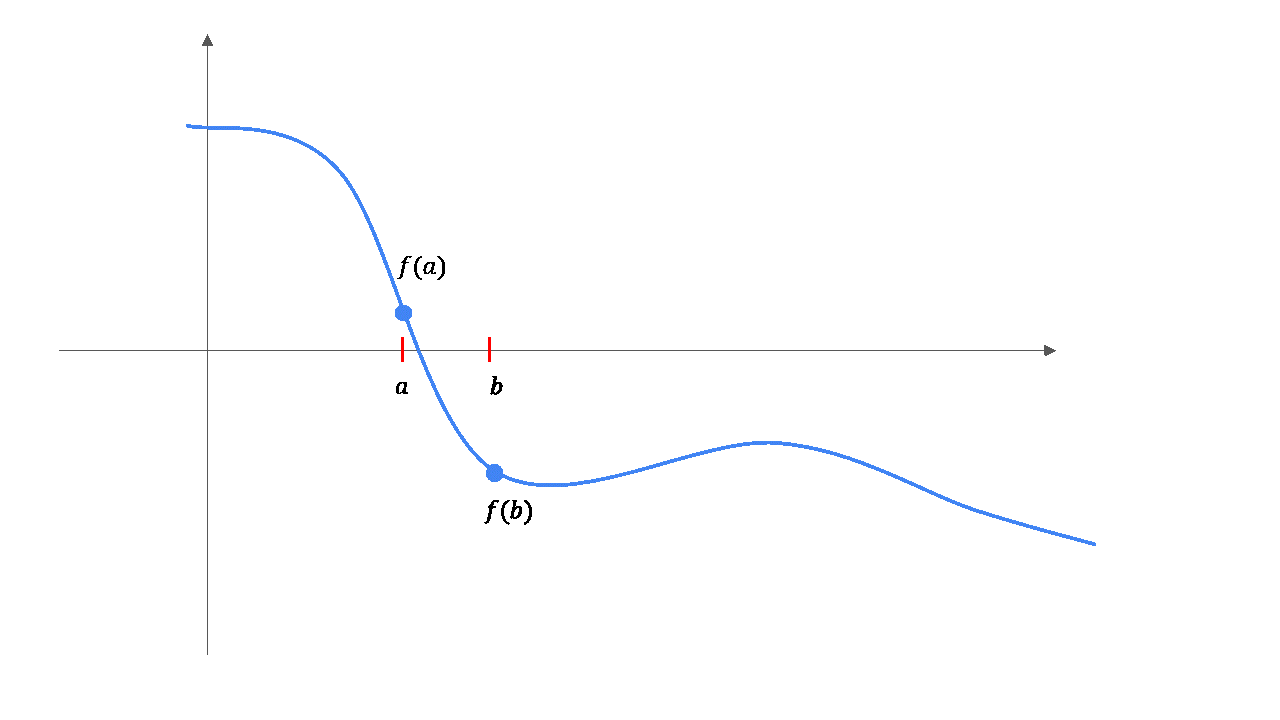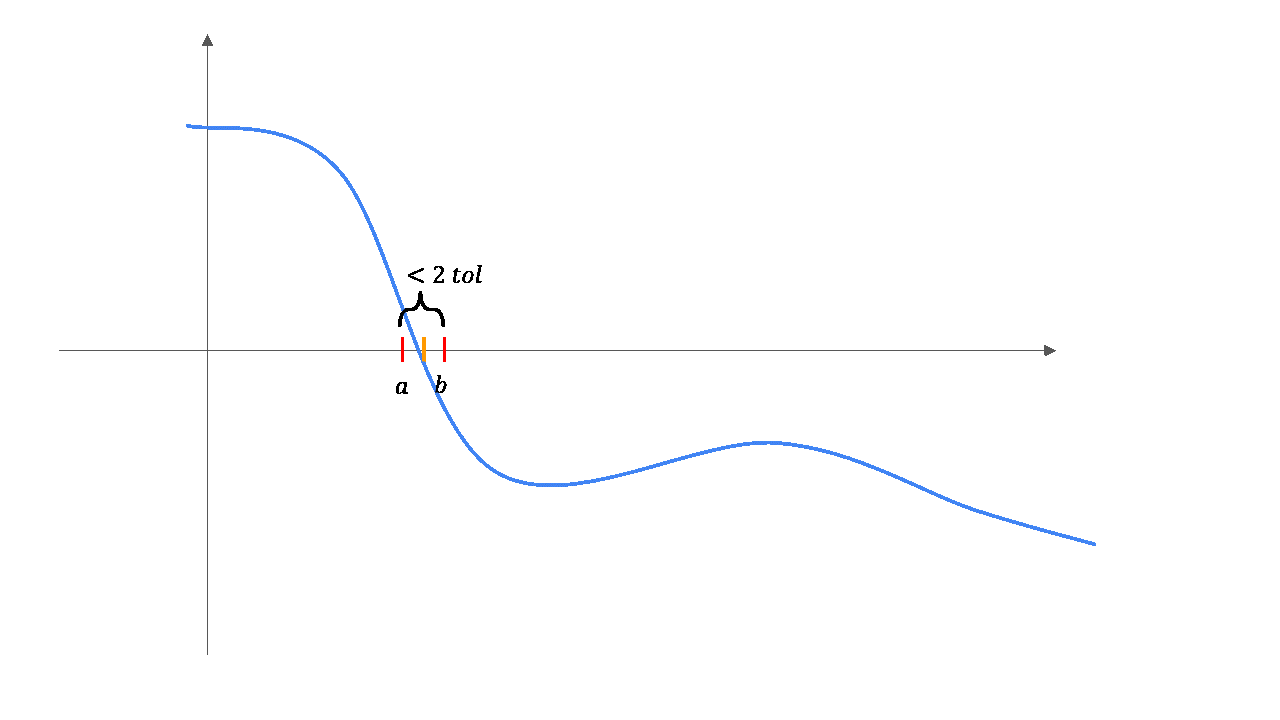
Beispiel: Bisektionsverfahren¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | #include <stdio.h>
double f(double x) {
return x*x + 1/(2 + x) - 2;
}
double bisection(double a, double b, double tol){
double m = 0.5*(a+b);
if ( b - a <= 2*tol ) {
return m;
}
else {
if ( f(a)*f(m) <= 0 ) {
return bisection(a,m,tol);
}
else {
return bisection(m,b,tol);
}
}
}
int main() {
double a = 0;
double b = 10;
double tol = 1e-12;
double x = bisection(a,b,tol);
printf("Approximate zero of the function x=%g\n",x);
printf("Function value f(x)=%g\n",f(x)); // %g chooses good floating point output
}
|
Approximate zero of the function x=1.30278 Function value f(x)=-5.64659e-13
Mathematische Funktionen¶
Deklaration der math. Funktionen in
math.h- Input & Output der Funktionen sind vom Typ
double
- Input & Output der Funktionen sind vom Typ
Wenn diese Funktionen benötigt werden
- im Source-Code:
#include <math.h> - Compilieren des Source-Code mit
zusätzlicher Linker-Option
-lm, d.h.gcc file.c -o output -lmerzeugt Executableoutput- moderne Compiler linken oft automatisch, d.h.,
-lmnicht nötig
- moderne Compiler linken oft automatisch, d.h.,
- im Source-Code:
Diese Bibliothek stellt u.a. zur Verfügung
- Trigonometrische Funktionen
cos,sin,tan,acos,asin,atan,cosh,sinh,tanh- Exponentialfunktion und Logarithmus
exp,log,log10- Potenz- und Wurzelfunktion
pow,sqrt(wobei )- Häufig ist explizite Berechnung effizienter:
- BSP: mittels
x * x * xberechnen - BSP: über
if ... elseberechnen: falls gerade, sonst - Absolutbetrag
fabs - Rundung auf ganze Zahlen:
round,floor,ceil
- ACHTUNG: In der Bibliothek
stdlib.hgibt esabsabsist Absolutbetrag fürint(ggf. type cast!)fabsist Absolutbetrag fürdouble
Preprocessor, Compiler & Linker¶
- Ein Compiler besteht aus mehreren Komponenten, die nacheinander abgearbeitet werden
Preprocessor wird intern gestartet, bevor der Source-Code compiliert wird
- Ersetzt Text im Code durch anderen Text
- Preprocessor-Befehle beginnen immer mit
#und enden nie mit Semikolon, z.B. #define text replacement- in allen nachfolgenden Zeilen wird der
Text
textdurchreplacementersetzt - zur Definition von Konstanten
- Konvention:
GROSS_MIT_UNDERSCORES
- in allen nachfolgenden Zeilen wird der
Text
#include file- einfügen der Datei
file
- einfügen der Datei
Compiler übersetzt (Source-)Code in Object-Code
- Object-Code = Maschinencode, bei dem symbolische Namen (z.B. Funktionsnamen) noch vorhanden sind
Weiterer Object-Code wird zusätzlich eingebunden
- z.B. Bibliotheken (= Sammlungen von Funktionen)
Linker ersetzt symbolische Namen im Object- Code durch Adressen und erstellt dadurch ein ausführbares Programm, sog. Executable
Bibliotheken & Header-Files¶
(Funktions-) Bibliothek (z.B. math. Funktionen) besteht immer aus 2 Dateien
- Object-Code
- zugehöriges Header-File
Im Header-File steht die Deklaration aller Fktn, die in der Bibliothek vorhanden sind
Will man Bibliothek verwenden, muss man zugehöriges Header-File einbinden
#include headerbindet Header-Fileheaderaus Standardverzeichnis/usr/include/ein,- z.B.
math.h(Header-File zur math. Bib.) #include "datei"bindet Datei aus aktuellem Verzeichnis ein (z.B. Downloads vom Internet)- idR. führt -Compiler
#include <stdio.h>von allein aus (in zugehöriger Bib. liegt z.B.printf)
Ferner muss man den Object-Code der Bibliothek hinzulinken
- Wo Object-Code der Bibliothek liegt, muss
gccmittels Option-l(und-L) mitgeteilt werden - z.B.
gcc file.c -lmlinkt Mathematik Bibliothek (Dateinamelibm.a) - Standardbibliotheken automatisch gelinkt,
z.B.
stdio(also keine zusätzliche Option nötig)
- Wo Object-Code der Bibliothek liegt, muss
Elementares Beispiel¶
- Preprocessor-Befehle in 1, 2 ohne Semikolon
- Compilieren mit
gcc sqrt.c -lm - Vergisst man
-lmFehlermeldung des Linkers
In function 'main'
sqrt.c:(.text+0x24): undefined reference to 'sqrt'
collect2: ld returned 1 exit status
1 2 3 4 5 6 7 8 | #include <stdio.h>
#include <math.h>
int main() {
double x = 2.;
double y = sqrt(x);
printf("sqrt(%f)=%f\n",x,y);
}
|
sqrt(2.000000)=1.414214
Code mehrfach ausführen mit Schleifen¶
Schleifen¶
- Schleifen führen einen oder mehrere Befehle wiederholt aus
- In Aufgabenstellung häufig Hinweise, wie
- Vektoren & Matrizen
- Laufvariablen
- Summen
- Produkte
- Text wie z.B. solange bis oder solange wie
- Man unterscheidet
- Zählschleifen
for: Wiederhole etwas eine gewisse Anzahl oft - Bedingungsschleifen
while, do...while: Wiederhole etwas solange, wie eine Bdg. gilt oder bis eine Bedingung gilt
- Zählschleifen
Die while-Schleife¶
Formal:
while( condition ) statement- "Solange wie etwas gilt, tue Folgendes:"
Vor jedem Durchlauf wird
conditiongeprüft & Abbruch, falls nicht erfüllt- sog. kopfgesteuerte Schleife
- Eventuell also kein einziger Durchlauf!
statementkann Block sein
1 2 3 4 5 6 7 8 9 10 11 | #include <stdio.h>
int main() {
int counter = 9;
while (counter > 0) {
printf("%d ",counter);
counter = counter-1;
}
printf("\n");
}
|
9 8 7 6 5 4 3 2 1
Operator ++¶
++aunda++sind arithmetisch äquivalent zua=a+1- Zusätzlich aber Auswertung von Variable
a - Präinkrement
++a- Erst erhöhen, dann auswerten
- Postinkrement
a++- Erst auswerten, dann erhöhen
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <stdio.h>
int main() {
int a = 0;
int b = 43;
printf("1) a=%d, b=%d\n",a,b);
b = a++;
printf("2) a=%d, b=%d\n",a,b);
b = ++a;
printf("3) a=%d, b=%d\n",a,b);
}
|
1) a=0, b=43 2) a=1, b=0 3) a=2, b=2
Operatoren ++ und --¶
Analog zu
a++und++agibt es- Prädekrement
--a- Erst verringern, dann auswerten
- Postdekrement
a--- Erst auswerten, dann verringern
- Prädekrement
Beachte Unterschied in Bedingungsschleife!
1 2 3 4 5 6 7 8 9 10 | #include <stdio.h>
int main() {
int counter = 5;
while (--counter > 0) {
printf("%d ",counter);
}
printf("\n");
}
|
4 3 2 1
Bisektionsverfahren (Wiederholung)¶
Gegeben: stetiges mit
- Toleranz
Tatsache: Zwischenwertsatz mind. eine Nst
- denn und haben versch. Vorzeichen
Gesucht: mit folgender Eigenschaft
- und
Bisektionsverfahren = iterierte Intervallhalbierung
- Solange wie Intervallbreite
- Berechne Intervallmittelpunkt und
- Falls , betrachte Intervall
- sonst betrachte halbiertes Intervall
- ist schließlich gesuchte Approximation
- Verfahren basiert nur auf Zwischenwertsatz
Terminiert nach endlich vielen Schritten, da jeweils Intervall halbiert wird
Konvergenz gegen Nullstelle für .
Bisektionsverfahren (mit Schleife statt Rekursion)¶
- Verwendung von Variablen
faundfmvermeidet doppelte Funktionsauswertung - Schleife ist idR. effizienter als Rekursion!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | #include <stdio.h>
#include <math.h>
double f(double x) {
return x*x + 1/(2 + x) - 2;
}
double bisection(double a, double b, double tol){
double fa = f(a);
double m = 0.5*(a+b);
double fm = 0;
while ( b - a > 2*tol ) {
m = 0.5*(a+b);
fm = f(m);
if ( fa*fm <= 0 ) {
b = m;
}
else {
a = m;
fa = fm;
}
}
return m;
}
int main() {
double a = 0;
double b = 10;
double tol = 1e-12;
double x = bisection(a,b,tol);
printf("Approximate zero of the function x=%g\n",x);
printf("Function value f(x)=%g\n",f(x));
}
|
Approximate zero of the function x=1.30278 Function value f(x)=-1.99352e-12
Euklidischer Algorithmus¶
- Gegeben: zwei ganze Zahlen
Gesucht: größter gemeinsamer Teiler
- engl. greatest common divisor (gcd)
Euklidischer Algorithmus:
- Falls , gilt
- Vertausche und , falls
- Dann gilt , denn:
- Sei Teiler von
- d.h. und mit ,
- also und
- d.h. teilt und
- d.h.
- analog
- Ersetze durch , wiederhole diese Schritte
- Erhalte nach endlich vielen Schritten:
- Falls , wird also pro Schritt um mindestens kleiner
- Nach endlichen vielen Schritten kann also nicht mehr gelten
- d.h. Algorithmus terminiert
Illustration des Euklidischen Algorithmus¶
- Wir berechnen mit dem Euklidischen Algorithms
- Die grauen Linien verdeutlichen, dass die Zwischenergebnisse immer den selben größten gemeinsamen Teiler haben

Euklidischer-Algorithmus¶
- berechnet gcd von
- basiert auf für
- Für terminiert
whilemit
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <stdio.h>
int main() {
int a = 200;
int b = 110;
int tmp = 0;
printf("gcd(%d,%d)=",a,b);
while (a != b) {
if (a < b) {
tmp = a;
a = b;
b = tmp;
}
a = a-b;
}
printf("%d\n",a);
}
|
gcd(200,110)=10
Euklid-Algorithmus (verbessert)¶
- Kernstück des Euklid-Algorithmus
1 2 3 4 5 6 7 8 | while (a != b) {
if (a < b) {
tmp = a;
a = b;
b = tmp;
}
a = a-b;
}
|
- Erinnerung:
a%bist Divsionsrest vona/b - Euklid-Algorithmus iteriert
a=a-bbis- d.h. bis
a=a%b - falls fertig, gilt
a=0und Ergebnisbist größter gemeinsamer Teiler
- d.h. bis
1 2 3 4 5 6 7 8 | while (a != 0) {
if (a < b) {
tmp = a;
a = b;
b = tmp;
}
a = a%b;
}
|
- Divisionsrest erfüllt immer
a%b < b- d.h. es wird immer vertauscht nach Rechnung
- falls fertig, gilt
b=0und Ergebnisaist größter gemeinsamer Teiler
1 2 3 4 5 | while (b != 0) {
tmp = a%b;
a = b;
b = tmp;
}
|
Beispiel: Euklidischer Algorithmus (verbessert)¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | #include <stdio.h>
int main() {
int a = 200;
int b = 110;
int tmp = 0;
printf("ggT(%d,%d)=",a,b);
while (b != 0) {
tmp = a%b;
a = b;
b = tmp;
}
printf("%d\n",a);
}
|
ggT(200,110)=10
Die do-while-Schleife¶
Formal:
do statement while( condition );- "Tue Folgendes, solange wie etwas gilt:"
Nach jedem Durchlauf wird
conditiongeprüft & Abbruch, falls nicht erfüllt- sog. fußgesteuerte Schleife
- Also mindestens ein Durchlauf!
statementkann Block sein
1 2 3 4 5 6 7 8 9 10 11 | #include <stdio.h>
int main() {
int counter = 5;
do {
printf("%d ",counter);
}
while (--counter>0);
printf("\n");
}
|
5 4 3 2 1
Ein weiteres Beispiel¶
Fibonacci-Folge strebt gegen unendlich
- , und für
Ziel: Berechne erstes Folgenglied mit für gegebene Schranke
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | #include <stdio.h>
int main() {
int x0 = 0;
int x1 = 1;
int tmp = 0;
int c = 0;
printf("c=");
scanf("%d",&c);
printf("%d %d ",x0,x1);
do {
tmp = x0 + x1;
x0 = x1;
x1 = tmp;
printf("%d ",x1);
}
while(x1 <= c);
printf("\n");
}
|
c=5 0 1 1 2 3 5 8
"solange wie" vs. "solange bis"¶
breakbeendet die aktuelle Schleifewhilehat Laufbedingungcondition- d.h. Schleife läuft, solange wie
conditionwahr
- d.h. Schleife läuft, solange wie
Algorithmen haben idR. Abbruchbedingung
done- d.h. Abbruch, falls
donewahr - d.h.
conditionNegation vondone
- d.h. Abbruch, falls
einfache Realisierung über Endlosschleife mit
break- Bedingung in Zeile 11 ist immer wahr!
- Abbruch erfolgt nur durch
breakin Zeile 13
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | #include <stdio.h>
int main() {
int a = 200;
int b = 110;
int tmp = 0;
printf("gcd(%d,%d)=",a,b);
// Euclidean algorithm with infinite loop + break
while (1) {
if (b == 0) {
break;
}
else {
tmp = a%b;
a = b;
b = tmp;
}
}
printf("%d\n",a);
}
|
gcd(200,110)=10
Einfache Fehlerkontrolle¶
Motivation¶
- Fakt ist: alle Programmierer machen Fehler
- Code läuft beim ersten Mal nie richtig
- Großteil der Entwicklungszeit geht in Fehlersuche
- "Profis" unterscheiden sich von "Anfängern" im Wesentlichen durch effizientere Fehlersuche
- Syntax-Fehler sind leicht einzugrenzen
- es steht Zeilennummer dabei (Compiler!)
- Tipp: Verwende während des Programmierens zum Syntax-Test regelmäßig (Details später!)
gcc -c name.cnur Objekt-Codegcc -c -Wall name.calle Warnungen
- Laufzeitfehler sind viel schwieriger zu finden
- Programm läuft, tut aber nicht das Richtige
- manchmal fällt der Fehler ewig nicht auf sehr schlecht
Fehler vermeiden!¶
- Programmier-Konventionen beachten
- z.B. bei Namen für Variablen, Funktionen etc.
- Kommentarzeilen dort, wo im Code etwas passiert
- z.B. Verzweigung mit nicht offensichtlicher Bdg.
- z.B. Funktionen (Zweck, Input, Output)
jede Funktion hat nur eine Funktionalität
- jede Funktion einzeln & sofort testen
- Wenn später Funktion verwendet wird, kann ein etwaiger Fehler dort nicht mehr sein!
- d.h. kann Fehler im Programm schneller lokalisieren!
jede Funktionalität hat eigene Funktion
- Programm in überschaubare Funktionen zerlegen!
- nicht alles auf einmal programmieren!
- Achtung: Häufiger Anfängerfehler!
- Möglichst viele Fehler bewusst abfangen!
- Funktions-Input auf Konsistenz prüfen!
- Fehler-Abbruch, falls inkonsistent!
- garantieren, dass Funktions-Output zulässig!
- Funktions-Input auf Konsistenz prüfen!
Bibliothek assert.h¶
- Ziel: Sofortabbruch mit Fehlermeldung, sobald Funktion merkt, dass Input / Output unzulässig
#include <assert.h>assert(condition)liefert Fehlerabbruch, fallsconditionfalsch- mit Ausgabe der Zeilennummer im Source-Code
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <stdio.h>
#include <assert.h>
void test(int x, int y) {
assert(x<y);
printf("It holds x < y\n");
}
int main() {
int x = 0;
int y = 0;
printf("x = ");
scanf("%d",&x);
printf("y = ");
scanf("%d",&y);
test(x,y);
}
|
x = 6 y = 3
tmp0re3hp7h.out: /tmp/tmpdnqxpqyp.c:5: test: Assertion `x<y' failed. [C kernel] Executable exited with code -6
Beispiel: Euklidischer Algorithmus¶
assertstellt sicher, dass Input zulässig- d.h. ist notwendig!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | #include <stdio.h>
#include <assert.h>
// The Euclidean algorithm to compute the greatest
// common divisor (gcd) is based on gcd(a,b) = gcd(a-b,b)
// for a>b and gcd(a,b) = gcd(b,a).
int euclid(int a, int b) {
assert(a > 0);
assert(b > 0);
int tmp = 0;
// iteration gcd(a,b) = gcd(a-b,b), realized
// using division with remainder, until b = 0.
// Then, since it was a==b, it holds gcd = a.
while (b != 0) {
tmp = a%b;
a = b;
b = tmp;
}
return a;
}
int main(){
int a=0,b=0;
printf("Input:\na=");
scanf("%d",&a);
printf("b=");
scanf("%d",&b);
printf("gcc(%d,%d) = %d\n",a,b,euclid(a,b));
}
|
Input: a=7 b=5 gcc(7,5) = 1
Testen von Code¶
Motivation¶

- Ariane 5 Explosion ('96)
- Konversion
doubleint - Schaden ca. Mio. Dollar
- Konversion
- Patriot Missile Fehler, Golfkrieg ('91)
- Zeitmessung falsch berechnet & Rundungsfehler
- Untergang Sleipner A offshore Plattform ('91)
- Fehler in der Finite-Elemente-Berechnung
- Kosten ca Mio. EUR
- "kleine BUGs, große GAUs"
Qualitätssicherung¶
- Software entsteht durch menschliche Hand
- Fehler zu machen, ist menschlich!
- Software wird deshalb Fehler enthalten
- Ziel: (Laufzeit-) Fehler finden vor großem Schaden
- Je später Fehler entdeckt werden, desto aufwändiger ist ihre Behebung!
- Schon beim Implementieren auf Qualität achten
- siehe oben: Fehler vermeiden!
- wünschenswert: je 1/3 Zeit für
- Programmieren
- Testen
- Dokumentieren
- wünschenswert: Dokumentation der Tests!
- damit reproduzierbar
- In der Praxis meist viel Programmieren, wenig Testen, noch weniger Dokumentieren ;-)
Testen¶
Testen ist der Prozess, ein Programm mit der Absicht auszuführen, Fehler zu finden!
- Glenford Myers: Art of Software Testing (1979)
Test ist der Vergleich des Verhaltens eines Prg (Ist) mit dem erwarteten Verhalten eines Systems (Soll)
Es ist praktisch nicht möglich, alle Programmfunktionen und
alle möglichen Werte in den Eingabedaten in allen Kombinationen zu testen.- d.h. Tests sind idR. unvollständig!
- Probleme beim unvollständigen Testen
- Tests erlauben nur das Auffinden von Fehlern
- Tests können Korrektheit nicht beweisen
- Fehlerursache ist durch Soll-Ist-Vergleich nicht zwangsläufig klar
- Testfälle können selbst fehlerhaft sein!
- Vorteile beim unvollständigen Testen
- Zeitaufwand vertretbar
- Tests beziehen sich idR. auf "realistischen Input"
- Tests sind idR. reproduzierbar
Arten von Tests¶
strukturelle Tests (für jede Funktion)
- Werden alle Anweisungen ausgeführt oder gibt es toten Code?
- Treten Fehler auf, wenn
if ... elsemit wahr / falsch durchlaufen werden?
funktionale Tests (für jede Fkt. und Programm)
- Tut jede Funktion mit zulässigen Parametern das Richtige? (d.h. Ergebnis korrekt?)
- Tut das Programm (bzw. Teilabschnitte) das Richtige? (d.h. Ergebnis korrekt?)
- Werden unzulässige Parameter erkannt?
- Werden Grenzfälle / Sonderfälle korrekt erkannt und liefern das Richtige?
- Was passiert bei Fehleingaben, d.h. bei Fehler des Benutzers?
Funktionale Tests?¶
- Ziel: Tut Funktion / Programm das Richtige?
- funktionale Tests brauchen Testfälle
- mit bekanntem Ergebnis / Output
- Was sind generische Fälle / Parameter?
- Bei welchen Fällen treten Verzweigungen auf?
- Möglichst viele Verzweigungen abdecken!
- Welche Fälle sind kritisch?
- Zahlen werden im Rechner nicht exakt dargestellt (später mehr!)
- Außerdem keine exakte Arithmetik bei
double!- jede
double-Rechnung hat Rechenfehler!
- jede
- Wo können aufgrund solcher Rechenfehler andere Ergebnisse auftreten?
- z.B. Ist ein Punkt auf dem Kreisrand?
- früh mit dem Testen beginnen
- nach Implementierung jeder Funktion!
- nicht erst dann, wenn Prg komplett fertig!
- nach Code-Korrektur alle(!) Tests wiederholen
- deshalb Dokumentation der Tests!
- Ab jetzt in der UE stets: Wie wurde getestet?
- allerdings nur inhaltlich
- d.h. ohne Fehleingaben des Nutzers
Daten speichern in Arrays¶
Vektoren sind 1D-Arrays¶
Deklaration eines Vektors :
double x[N];xistdouble-Vektor
Zugriff auf Komponenten:
x[j]entspricht- Jedes
x[j]ist vom Typdouble
Analoge Deklaration für andere Datentypen
int y[N];yistint-Vektor
- ACHTUNG mit der Indizierung der Komponenten
- Indizes in
- idR. Indizes in Mathematik
- Initialisierung bei Deklaration möglich:
double x[3] = {1,2,3};deklariert den Vektor
- Vektor-Initialisierung nur bei Deklaration erlaubt
- Später zwingend komponentenweises Schreiben!
- d.h.
x[0] = 1; x[1] = 2; x[2] = 3;ist OK! x = {1,2,3}ist verboten!
- d.h.
- Später zwingend komponentenweises Schreiben!
Beispiel: Einlesen eines Vektors¶
Ausgabe
doubleüberprintfmit Platzhalter%fEinlesen
doubleüberscanfmit Platzhalter%lf- Es gibt keine Möglichkeit, Vektoren als Ganzes einzulesen / auszugeben!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | #include <stdio.h>
int main() {
double x[3] = {0,0,0};
printf("Read a vector x in R^3 from keyboard:\n");
// read x0
printf("x_0 = ");
scanf("%lf",&x[0]);
// read x1
printf("x_1 = ");
scanf("%lf",&x[1]);
// read x2
printf("x_2 = ");
scanf("%lf",&x[2]);
// print vector (componentwise)
printf("x = (%f, %f, %f)\n",x[0],x[1],x[2]);
}
|
Read a vector x in R^3 from keyboard: x_0 = 3 x_1 = 4 x_2 = 5 x = (3.000000, 4.000000, 5.000000)
Achtung: Statische Arrays¶
- Die Länge von Arrays ist statisch
- nicht veränderbar während Programmablauf
- kann nicht zu erweitert werden
- Programm kann nicht selbständig herausfinden,
wie groß ein Array ist
- d.h. Programm weiß bei Ablauf nicht, dass Vektor Länge hat
- Muss bei der Programmierung beachtet werden!
- Achtung mit Indizierung!
- Indizes laufen in C
- Prg kann nicht wissen, ob
x[j]definiert istxmuss mindestens Länge haben!- falsche Indizierung ist kein Syntaxfehler!
- sondern ggf. ein Laufzeitfehler!
- Arrays dürfen nicht Output einer Funktion sein!
- Das ist auch kein Problem, denn:
- Arrays werden mit Call by Reference an eine Funktion übergeben!
- Erklärung folgt später ( Pointer!)
Arrays & Call by Reference¶
Man sieht: Call by Reference bei Vektoren!
- Erklärung folgt später ( Pointer!)
in Funktionssignatur darf man Vektorlänge weglassen
- Programmierer für korrekten Zugriff zuständig!
void allByReference(double y[])auch OK!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | #include <stdio.h>
void callByReference(double y[3]) {
printf("a) y = (%f, %f, %f)\n",y[0],y[1],y[2]);
y[0] = 1;
y[1] = 2;
y[2] = 3;
printf("b) y = (%f, %f, %f)\n",y[0],y[1],y[2]);
}
int main() {
double x[3] = {0,0,0};
printf("c) x = (%f, %f, %f)\n",x[0],x[1],x[2]);
// function call modifies the coefficients!
callByReference(x);
printf("d) x = (%f, %f, %f)\n",x[0],x[1],x[2]);
}
|
c) x = (0.000000, 0.000000, 0.000000) a) y = (0.000000, 0.000000, 0.000000) b) y = (1.000000, 2.000000, 3.000000) d) x = (1.000000, 2.000000, 3.000000)
Falsche Indizierung von Vektoren¶
Zeile 7, 10: Falscher Zugriff auf Vektor
x,- d.h. Laufzeitfehler
- ggf. werden andere Daten überschrieben!
- Trotzdem keine Fehlermeldung/Warnung vom Compiler!
- Für korrekte Indizes sorgt der Programmierer!
- d.h. Laufzeitfehler
Bei kleinen Überschreitungen der Arraylänge oft keine Fehlermeldung. Wenn man aber 100 mit 10000 ersetzt, dann stürzt das Programm ab.
- weil Betriebssystem merkt, dass das Programm "aus dem Ruder läuft"!
- d.h. Programm greift auf Speicherbereiche zu, die ihm nicht zugeordnet / erlaubt sind.
1 2 3 4 5 6 7 8 9 10 11 | #include <stdio.h>
int main() {
int x[3] = {0,1,2};
// this coefficient has no reserved memory!
x[100] = 43;
// nevertheless, writing and reading is possible!
printf("x = (%d, %d, %d), x[%d] = %d\n", x[0],x[1],x[2],100,x[100]);
}
|
x = (0, 1, 2), x[100] = 43
Matrizen¶
- Matrix ist rechteckiges Schema
mit Koeffizienten
- zentrale math. Objekte der Linearen Algebra
Deklaration einer Matrix :
double A[M][N];
Zugriff auf Komponenten:
A[j][k]entspricht- Jedes
A[j][k]ist vom Typdouble
zeilenweise Initialisierung bei Deklaration möglich:
double A[2][3] = {{1,2,3},{4,5,6}};deklariert + initialisiert- Nur bei gleichzeitiger Deklaration erlaubt, vgl. Vektoren
Allgemeine Arrays¶
- Vektor ist ein -dim. Array
- Matrix ist ein -dim. Array
- Ist
typeDatentyp, so deklarierttype x[N];einen Vektor der Länge- Koeffizienten
x[j]sind Variablen vom Typtype
- Ist
typeDatentyp, so deklarierttype x[M][N];eine Matrixx[j]ist Vektor vom Typtype(der Länge )- Koeff.
x[j][k]sind Variablen vom Typtype
- Auch mehr Indizes möglich
type x[M][N][P];deklariert -dim. Arrayx[j]ist Matrix vom Typtypex[j][k]ist Vektor vom Typtype(der Länge )- Koeff.
x[j][k][p]sind Variablen vom Typtype
- etc.
- Arrays dürfen nicht Output einer Funktion sein!
- Arrays werden mit Call by Reference an eine Funktion übergeben!
Zählschleifen¶
Die for-Schleife¶
for (init.; cond.; step-expr.)statement- Ablauf einer
for-Schleife- (1) Ausführen der Initialisierung
init. - (2) Abbruch, falls Bedingung
cond.nicht erfüllt - (3) Ausführen von
statement - (4) Ausführen von
step-expr. - (5) Sprung nach (2)
- (1) Ausführen der Initialisierung
statementist- entweder eine logische Programmzeile
- oder mehrere Programmzeilen als Block
{...},
in C ist
foreigentlich eine Bedingungsschleife- trotzdem immer
forverwenden, um Statement "eine fixe Anzahl" oft zu wiederholen - gut programmiert = leicht verständlicher Code!
- trotzdem immer
1 2 3 4 5 6 7 8 9 10 11 | #include <stdio.h>
int main() {
int j = 0;
for (j=5; j>0 ; j--) {
printf("%d ",j);
}
printf("\n");
}
|
5 4 3 2 1
Vektor einlesen & ausgeben¶
- Funktionen müssen Länge von Arrays kennen!
- d.h. zusätzlicher Input-Parameter nötig
- Arrays werden mit Call by Reference übergeben!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | #include <stdio.h>
// Read from the keyboard a double vector
// of length dim
void scanVector(double input[], int dim) {
int j = 0;
// iterate over all indices of the vector
for (j=0; j<dim; j++) {
// initialize j-th coefficient
input[j] = 0;
// read j-th coefficient
printf("%d: ",j);
scanf("%lf",&input[j]);
}
}
// Print to the screen a double vector
// of length dim
void printVector(double output[], int dim) {
int j = 0;
// iterate over all indices of the vector
for (j=0; j<dim; j++) {
// print j-th coefficient
printf("%f ",output[j]);
}
printf("\n");
}
int main() {
double x[5];
// recall: call by reference for arrays
scanVector(x,5);
printVector(x,5);
}
|
0: 8 1: 6 2: 5 3: 4 4: 5 8.000000 6.000000 5.000000 4.000000 5.000000
Minimum eines Vektors¶
- Hinweise zur Realisierung (vgl. UE)
- Vektorlänge ist Konstante im Hauptprogramm
- d.h. Länge im Hauptprogramm nicht veränderbar
- aber Input z.B. der Funktion scanVector
- d.h. Funktion arbeitet für beliebige Länge
- Vektorlänge ist Konstante im Hauptprogramm
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 | #include <stdio.h>
#define DIM 5
void scanVector(double input[], int dim) {
int j = 0;
for (j=0; j<dim; j++) {
input[j] = 0;
printf("%d: ",j);
scanf("%lf",&input[j]);
}
}
// The function returns the minimum of a double vector
// of length dim
double min(double input[], int dim) {
int j = 0;
// initial guess: the minimum is located at input[0]
double minval = input[0];
// iterate over all entries of the vector
for (j=1; j<dim; j++) {
// if a smaller value is found, update minimum
if (input[j] < minval) {
minval = input[j];
}
}
return minval;
}
int main() {
double x[DIM];
scanVector(x,DIM);
printf("The minimum of the vector is %f\n", min(x,DIM));
}
|
0: 3 1: 4 2: 5 3: 6 4: 7 The minimum of the vector is 3.000000
Beispiel: Summensymbol ¶
Berechnung der Summe :
- Abkürzung
Definiere theoretische Hilfsgröße
Dann gilt
- etc.
Realisierung also durch -maliges Aufsummieren
- ACHTUNG: Zuweisung, keine Gleichheit
S = a_1S = S + a_2S = S + a_3etc.
- ACHTUNG: Zuweisung, keine Gleichheit
Beispiel: Summensymbol ¶
Programm berechnet für .
ACHTUNG: Bei iterierter Summation nicht vergessen, Ergebnisvariable auf Null zu setzen vgl. Zeile 7
- Anderenfalls: Falsches/Zufälliges Ergebnis!
statt
sum = sum + j;- Kurzschreibweise
sum += j;
- Kurzschreibweise
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <stdio.h>
int main() {
int j = 0;
int n = 100;
int sum = 0;
for (j=1; j<=n; j++) {
sum = sum+j;
}
printf("sum_{j=1}^{%d} j = %d\n",n,sum);
}
|
sum_{j=1}^{100} j = 5050
Beispiel: Produktsymbol ¶
Programm berechnet Faktorielle für .
ACHTUNG: Bei iteriertem Produkt nicht vergessen, Ergebnisvariable auf Eins zu setzen vgl. Zeile 7
- Anderenfalls: Falsches/Zufälliges Ergebnis!
statt
factorial = factorial*j;- Kurzschreibweise
factorial *= j;
- Kurzschreibweise
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <stdio.h>
int main() {
int j = 0;
int n = 5;
int factorial = 1;
for (j=1; j<=n; j++) {
factorial = factorial*j;
}
printf("%d! = %d\n",n,factorial);
}
|
5! = 120
Matrix-Vektor-Multiplikation¶
- Man darf
for-Schleifen schachteln- Typisches Beispiel: Matrix-Vektor-Multiplikation
- Seien Matrix, Vektor
- Def durch
- Indizierung in C startet bei
- Achtung: In Mathematik Indizierung idR. ab !
- ist also Schreibweise für lineares GLS
- Implementierung
- äußere Schleife über , innere für Summe
- ACHTUNG: Init.
b[j] = 0nicht vergessen!
1 2 3 4 5 6 | for (j=0; j<M; j++) {
b[j] = 0;
for (k=0; k<N; k++) {
b[j] = b[j] + A[j][k]*x[k];
}
}
|
Matrix spaltenweise speichern 1/2¶
mathematische Bibliotheken speichern Matrizen idR. spaltenweise als Vektor
- , gespeichert als
- , gespeichert als
muss Matrix spaltenweise speichern, wenn ich solche Bibliotheken nutzen will
- diese Bibliotheken (aus historischen Gründen) meist in Fortran programmiert
Beachte: C indiziert ,
- ist -tes Element der -ten Spalte
- also vorher Spalten mit Speicherplätzen
- plus Speicherplätze in der -ten Spalte
gezeigt: mit
BSP. BLAS (basic linear algebra subroutines)
- alles, was man mit Vektoren machen kann...
- elementare Operationen mit Matrizen...
- BSP. LAPACK (linear algebra package)
- lineare Gleichungssysteme lösen
- Eigenwerte berechnen
Matrix spaltenweise speichern 2/2¶
Erinnerung:
- , gespeichert als
- entspricht also mit
Matrix-Vektor-Produkt
- ,
- mit
double A[M][N];
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | // 2D-Array Speicherung
for (j=0; j<M; j++) {
b[j] = 0;
for (k=0; k<N; k++) {
b[j] = b[j] + A[j][k]*x[k];
}
}
// 1D-Array spaltenweise Speicherung
for (j=0; j<M; j++) {
b[j] = 0;
for (k=0; k<N; k++) {
b[j] = b[j] + A[j+k*M]*x[k];
}
}
|
MinSort (= Selection Sort)¶
- Gegeben: Ein Vektor
Ziel: Sortiere , sodass
Algorithmus (1. Schritt)
- suche Minimum von
- vertausche und , d.h. ist kleinstes Elt.
- Algorithmus (2. Schritt)
- suche Minimum von
- vertausche und , d.h. zweit kleinstes Elt.
- nach Schritten ist sortiert
- Hinweise zur Realisierung (vgl. UE)
- Länge ist Konstante im Hauptprogramm
- i d.h. ist im Hauptprg nicht veränderbar
- aber ist Inputparameter der Funktion \texttt{minsort}
- i d.h. Funktion arbeitet für beliebige Länge
MinSort¶
- üblich: Kommentar, was eine Funktion tut, bei Vorwärts-Deklaration (Zeile 4--11)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 | #include <stdio.h>
#define DIM 5
// read a double vector of length dim from the keyboard
void scanVector(double input[], int dim);
// print a double vector of length dim to the screen
void printVector(double output[], int dim);
// sort a double vector of length dim in ascending order
void minsort(double vector[], int dim);
int main() {
double x[DIM];
scanVector(x,DIM);
minsort(x,DIM);
printVector(x,DIM);
}
void scanVector(double input[], int dim) {
int j = 0;
for (j=0; j<dim; j++) {
input[j] = 0;
printf("%d: ",j);
scanf("%lf",&input[j]);
}
}
void printVector(double output[], int dim) {
int j = 0;
for (j=0; j<dim; j++) {
printf("%f ",output[j]);
}
printf("\n");
}
void minsort(double vector[], int dim) {
int j = 0;
int k = 0;
int argmin = 0;
double tmp = 0;
// iterate over all indices of the vector
for (j=0; j<dim-1; j++) {
// determine minimum in (vector[j],...,vector[dim-1])
// initial guess: minimum is located at vector[j]
argmin = j;
for (k=j+1; k<dim; k++) {
if (vector[argmin] > vector[k]) {
argmin = k;
}
}
// now vector[argmin] is minimum in the remainder
// if needed, swap with j so that vector[j] is mininum
if (argmin > j) {
tmp = vector[argmin];
vector[argmin] = vector[j];
vector[j] = tmp;
}
}
}
|
0: 3 1: 4 2: 5 3: 6 4: 7 3.000000 4.000000 5.000000 6.000000 7.000000
break und continue¶
continueundbreakimstatementvon Schleifencontinuebeendet aktuellen Durchlaufbreakbeendet nur die aktuelle Schleife
Code ist schlecht programmiertes Beispiel!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <stdio.h>
int main() {
int j = 0;
int k = 0;
for (j=0; j<4; ++j) {
if (j%2 == 0) {
continue;
}
for (k=0; k < 10; ++k) {
printf("j=%d, k=%d\n",j,k);
if (k > 1) {
break;
}
}
}
printf("End: j=%d, k=%d\n",j,k);
}
|
j=1, k=0 j=1, k=1 j=1, k=2 j=3, k=0 j=3, k=1 j=3, k=2 End: j=4, k=2
Aufwand von Algorithmen¶
Aufwand eines Algorithmus¶
- wichtige Kenngröße für Algorithmen
- um Algorithmen zu bewerten / vergleichen
- Aufwand = Anzahl benötigter Operationen
- Zuweisungen
- Vergleiche
- arithmetische Operationen
- programmspezifische Operationen nicht gezählt
- Deklarationen & Initialisierungen
- Schleifen, Verzweigungen etc.
- Zählvariablen in Schleifen
- Aufwand wird durch "einfaches" Zählen ermittelt
- Konventionen zum Zählen nicht einheitlich
- in EPROG ist Aufwand für worst case interessant
- d.h. maximaler Aufwand im schlechtesten Fall
- häufig ist auch "mittlerer Aufwand" interessant
(d.h. Erwartungswert des Aufwands)
- mathematisch komplizierter
- deshalb nicht in EPROG
- in EPROG (maximal) benötigte Formeln:
Beispiel: Maximum suchen¶
Beim Zählen wird jede Schleife zu einer Summe!
- d.h.
forin Zeile 6 ist
- d.h.
Aufwand:
- Zuweisung Zeile 5
- In jedem Schritt der
for-Schleife Zeile 6--10- Vergleich Zeile 7
- Zuweisung (worst case!) Zeile 8
insgesamt Operationen
wobei Zählvariable nicht in Aufwand eingeht, d.h. nur Statement der
for-Schleife wird berücksichtigt
1 2 3 4 5 6 7 8 9 10 11 12 13 | double maximum(double vector[], int n) {
int i = 0;
double max = 0;
max = vector[0];
for (i=1; i<n; i++) {
if (vector[i] > max) {
max = vector[i];
}
}
return max;
}
|
Landau-Symbol (= groß-O)¶
- oft nur Größenordnung des Aufwands interessant
Schreibweise für
- heißt
- d.h. es existiert eine Konstante mit
i für .
d.h. wächst höchstens so schnell wie für
- Beispiel: Maximum suchen
- Aufwand für
- häufig entfällt "für "
- dann Grenzwert kanonisch z.B.
- Sprechweise (nur Beispiele):
- Algorithmus hat linearen Aufwand,
falls Aufwand bei Problemgröße
- Maximumssuche hat linearen Aufwand
- Algorithmus hat fastlinearen Aufwand,
falls Aufwand bei Problemgröße
- Die schnellsten Sortieralgorithmen (z.b. Quick-Sort, Merge-Sort) haben fast-linearen Aufwand)
- Algorithmus hat quadratischen Aufwand,
falls Aufwand bei Problemgröße
- Matrix-Vektor Multiplikation hat quadratischen Aufwand
- Algorithmus hat kubischen Aufwand,
falls Aufwand bei Problemgröße
- Gauss Elimination hat kubischen Aufwand
- Algorithmus hat exponentiellen Aufwand falls Ausfwand für bei Problemgröße
- Primfaktorzerlegung mittels Sieb-von-Erastostenes einer -stelligen Zahl hat exponentiellen Aufwand. Die schnellsten Algorithmen (Zahlkörpersieb) sind nicht viel schneller.
- Algorithmus hat linearen Aufwand,
falls Aufwand bei Problemgröße
Matrix-Vektor Multiplikation¶
In jedem Schritt der -Schleife Zeile 6--11
- Zuweisung Zeile 7
- In jedem Schritt der -Schleife Zeile 8--10
- Multiplikationen Zeile 9
- Additionen Zeile 9
- Zuweisung Zeile 9
insgesamt Operationen
- Aufwand
- bzw. Aufwand für
- d.h. quadratischer Aufwand für
1 2 3 4 5 6 7 8 9 10 11 12 | void MVM(double A[], double x[], double b[],
int m, int n) {
int i = 0;
int j = 0;
for (j=0; j<m; j++) {
b[j] = 0;
for (k=0; k<n; k++) {
b[j] = b[j] + A[j+k*m]*x[k];
}
}
}
|
Suchen im Vektor¶
- Aufgabe:
- Suche Index
jmitvector[j] == value - Rückgabe
-1, falls solcher nicht existiert
- Suche Index
in jedem Schritt der -Schleife
- 1 Vergleich
Anzahl der Operationen
- Aufwand im worst case
1 2 3 4 5 6 7 8 9 10 11 12 | int search(int vector[], int value, int n) {
int j = 0;
for (j=0; j<n; j++) {
if (vector[j] == value) {
return j;
}
}
return -1;
}
|
Binäre Suche im sortierten Vektor¶
- Voraussetzung: Vektor ist aufsteigend sortiert
Modifiziere Idee des Bisektionsverfahrens
- d.h. natürliche Suche im Telefonbuch
- Betrachte halben Vektor, falls
vector[j]!= value
Frage: Wieviele Iterationen hat der Algorithmus?
- jeder Schritt halbiert Vektor
- Falls Zweierpotenz, gilt
- dann maximal Schritte
- i je 2 Vergl. + 2 Zuw. + 1 Mult. + 2 Add./Subtr.
Aufwand , d.h. logarithmischer Aufwand
- sog. sublinearer Aufwand
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | int binsearch(int vector[], int value, int n) {
int j = 0;
int start = 0;
int end = n-1;
while (start <= end) {
j = 0.5*(end + start);
if (vector[j] == value) {
return j;
}
else if (vector[j] > value) {
end = j-1;
}
else {
start = j+1;
}
}
return -1;
}
|
Minsort¶
- In jedem Schritt der -Schleife
- Zuweisung
- In jedem Schritt der -Schleife
- Vergleich
- Zuweisung (worst case!)
- jeweils Vergleich
- jeweils Zuweisungen (worst case!)
- quadratischer Aufwand , weil:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | void minsort(int vector[], int n) {
int j = 0;
int k = 0;
int argmin = 0;
double tmp = 0;
for (j=0; j<n-1; j++) {
argmin = j;
for (k=j+1; k<n; k++) {
if (vector[argmin] > vector[k]) {
argmin = k;
}
}
if (argmin > j) {
tmp = vector[argmin];
vector[argmin] = vector[j];
vector[j] = tmp;
}
}
}
|
Aufwand & Rechenzeit¶
Jede Operation kostet Rechenzeit
- d.h. Aufwand korrespondiert zu Rechenzeit
Frage: Welche Rechenzeit kann ich erwarten?
- Antwort kann nur eine relative Größe sein, da Rechner unterschiedlich schnell
- theoretische Voraussagen
- linearer Aufwand
- Problemgröße Operationen
- Problemgröße Operationen
- d.h. Problemgröße Rechenzeit
- quadratischer Aufwand
- Problemgröße Operationen
- Problemgröße Operationen
- d.h. Problemgröße Rechenzeit
- etc.
- linearer Aufwand
BSP. Code braucht Sekunde für
- Aufwand Sekunden für
- Aufwand Sekunden für
- Aufwand Sek. für
Zeitmessung¶
- Wozu Zeitmessung?
- Vergleich von Algorithmen / Implementierungen
- Überprüfen theoretischer Voraussagen
- Bibliothek
time.h- Datentyp
clock_tfür Zeitvariablen für Ausgabe Typecast nicht vergessen! - Funktion
clock()liefert Rechenzeit seit Programmbeginn - Konstante
CLOCKS_PER_SECzum Umrechnen:Zeitvariable/CLOCKS_PER_SECliefert Angabe in Sekunden
- Datentyp
Beispiel: Zeitmessung¶
- einbinden Codes von Folie 115--117 (Zeile 15--17)
- dynamische Vektoren (Zeile 27--29) später!
- ersetzt nur
int vector[NMAX];
- ersetzt nur
auch Test mit Zufallszahlen manchmal sinnvoll
- hier auskommentiert (Zeile 38--44)
Bibliothek
time.htime(NULL)gibt Zeit seit 01.01.1970 in Sekunden- Fun fact: im Jahr 2038 reicht der Speicherplatz des Datentyps nicht mehr aus und es kommt zum Überlauf UNIX 2028 Bug (siehe Zahldarstellung im Computer später)
Bibliothek
stdlib.hsrand(time(NULL)): Initialisierung des Zufallszahlen-GeneratorsRAND_MAX: maximale Zufallszahl (Konstante)rand()liefertintZufallszahl von bisRAND_MAX
Vektor-Länge wächst
- Zeit wächst linear bzw. quadratisch
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 | //%cflags:-I data/
//ACHTUNG: Zeile 1 ist nur fuer die korrekte Funktion des interaktiven Skriptums noetig
// include some libraries
#include <stdio.h>
#include <math.h>
#include <time.h>
// include library for dynamic storage allocation
// see line 27-29 below
#include <stdlib.h>
// define minimal and maximal problem size
#define NMIN (int)1e3
#define NMAX (int)1e6
// declaration of codes from previous slides
#include "aufwand_search.c"
#include "aufwand_binsearch.c"
#include "aufwand_minsort.c"
int main() {
int n = NMIN;
int j = 0;
int tmp=0;
clock_t start = 0;
clock_t runtime = 0;
clock_t previous_runtime = 0;
// allocate dynamic vector ==> int vector[NMAX];
printf("*** allocate integer vector, length=%d\n",NMAX);
int* vector = malloc(NMAX*sizeof(int));
// initialize vector with deterministic data
printf("*** initialize vector\n");
for (j=0; j<NMAX; ++j) {
vector[j] = j;
}
/*
// alternative: initialize vector with random numbers
srand(time(NULL));
// fill the vector with non-negative random numbers
printf("*** generate random numbers\n");
for (j=0; j<NMAX; ++j) {
vector[j] = rand();
}
*/
// print the runtime for various vector lengths
printf("*** determine computing times\n");
for (n = NMIN; n <= NMAX; n = 2*n) {
// save start time, call function, determine runtime
start = clock();
tmp = search(vector,-1,n); // linear complexity
//tmp = binsearch(vector,-1,n); // logarithmic compl.
//minsort(vector,n); // quadratic complexity
runtime = clock() - start;
// print runtime (and relative increase of runtime)
if (n == NMIN) {
printf("n=%d, runtime=%1.2f\n",n,
(double) runtime/CLOCKS_PER_SEC);
}
else {
printf("n=%d, runtime=%1.2f, factor=%1.2f\n",
n, (double) runtime/CLOCKS_PER_SEC,
(double) runtime/previous_runtime);
}
previous_runtime = runtime;
}
}
|
/tmp/tmpr2qorgxe.c: In function ‘main’:
/tmp/tmpr2qorgxe.c:24:7: warning: variable ‘tmp’ set but not used [-Wunused-but-set-variable]
24 | int tmp=0;
| ^~~
*** allocate integer vector, length=1000000 *** initialize vector *** determine computing times n=1000, runtime=0.00 n=2000, runtime=0.00, factor=1.20 n=4000, runtime=0.00, factor=1.83 n=8000, runtime=0.00, factor=1.91 n=16000, runtime=0.00, factor=1.90 n=32000, runtime=0.00, factor=2.10 n=64000, runtime=0.00, factor=1.99 n=128000, runtime=0.00, factor=2.02 n=256000, runtime=0.00, factor=2.04 n=512000, runtime=0.00, factor=2.00
Vergleich von Laufzeit¶
| linear | quadratisch | fastlinear | |
|---|---|---|---|
| search | minsort | binsearch | |
| 1.000 | 0.00 | 0.00 | 0.00 |
| 2.000 | 0.00 | 0.00 | 0.00 |
| 4.000 | 0.00 | 0.01 | 0.00 |
| 8.000 | 0.00 | 0.06 | 0.00 |
| 16.000 | 0.00 | 0.25 | 0.00 |
| 32.000 | 0.00 | 1.03 | 0.00 |
| 64.000 | 0.00 | 4.12 | 0.00 |
| 128.000 | 0.00 | 16.55 | 0.00 |
| 256.000 | 0.00 | 64.31 | 0.00 |
| 512.000 | 0.00 | 257.25 | 0.00 |
| 1.024.000 | 0.00 | >18min | 0.00 |
| 2.048.000 | 0.01 | >72min | 0.00 |
| 4.096.000 | 0.01 | >4,5h | 0.00 |
| 8.192.000 | 0.02 | >18h | 0.00 |
| 16.384.000 | 0.04 | >3d | 0.00 |
| 32.768.000 | 0.08 | >12d | 0.00 |
| 65.536.000 | 0.15 | >1,5m | 0.00 |
| 131.072.000 | 0.29 | >6m | 0.00 |
| 262.144.000 | 0.60 | >2y | 0.00 |
| 524.288.000 | 1.18 | >8y | 0.00 |
| 1.048.576.000 | 2.53 | >32y | 0.00 |
Aufwand: Zusammenfassung¶
- Quadratischer Aufwand für große spürbar
- Fazit: Algorithmen sollen kleinen Aufwand haben
- Ziel der numerischen Mathematik
- nicht immer möglich, oft offene Frage, z.B., Aufwand für Lösen von LGS, oder in der theoretischen Informatik
Pointer¶
Variablen¶
Variable = symbolischer Name für Speicherbereich
- und Information, wie Speicherbereich interpretiert werden muss (Datentyp laut Deklaration)
Compiler übersetzt Namen in Referenz auf Speicherbereich und merkt sich, wie dieser interpretiert werden muss
Pointer¶
- Pointer = Variable, die Adresse eines Speicherbereichs enthält
- Dereferenzieren = Zugriff auf den Inhalt eines
Speicherbereichs mittels Pointer
- d.h. Schreiben eines Wertes an diese Adresse
bzw. Auslesen des dort gespeicherten Wertes
- Beim Dereferenzieren muss Compiler wissen, welcher Var.typ im gegebenen Speicherbereich liegt, d.h. wie Speicherbereich interpretiert werden muss
- d.h. Schreiben eines Wertes an diese Adresse
bzw. Auslesen des dort gespeicherten Wertes
Pointer in C¶
Pointer & Variablen sind in C eng verknüpft:
varVariable&varist zugehöriger PointerptrPointer*ptrist zugehörige Variable- insbesondere
*&var=varsowie&*ptr=ptr
Bei Deklaration muss Typ des Pointers angegeben werden, da
*ptreine Variable sein soll!int* ptr;deklariertptrals Pointer aufint- d.h.
ptrspeichert eine Adresse, an welcher einintim Speicher abgelegt ist
Wie üblich gleichzeitige Initialisierung möglich
int var;deklariert Variablevarvom Typintint* ptr = &var;deklariertptrund weist Speicheradresse der Variablevarzu- Bei solchen Zuweisungen muss der Typ von Pointer und Variable passen, sonst passiert Unglück (Laufzeitfehler)!
- I.a. gibt Compiler eine Warnung aus, z.B.
incompatible pointer type - Diese Warnung nie ignorieren, sondern Code checken, da 99\% Garantie auf Laufzeitfehler!
Analog für andere Datentypen, z.B.
double
Ein elementares Beispiel¶
%pPlatzhalter fürprintffür Adresse- manchmal sinnvoll zum Finden von Fehlern, dass man Werte von Variablen ausgibt!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <stdio.h>
int main() {
int var = 1;
int* ptr = &var;
printf("a) var = %d, *ptr = %d\n",var,*ptr);
var = 2;
printf("b) var = %d, *ptr = %d\n",var,*ptr);
*ptr = 3;
printf("c) var = %d, *ptr = %d\n",var,*ptr);
var = 47;
printf("d) *(&var) = %d,",*(&var));
printf("*&var = %d\n",*&var);
printf("e) &var = %p\n", &var);
}
|
a) var = 1, *ptr = 1 b) var = 2, *ptr = 2 c) var = 3, *ptr = 3 d) *(&var) = 47,*&var = 47 e) &var = 0x7fffc438a6ec
Begrifflichkeiten¶
Call by Value
- Funktionen erhalten Werte der Input-Parameter und speichern diese in lokalen Variablen
- Änderungen an den Input-Parameter wirken sich nicht außerhalb der Funktion aus
Call by Reference
- Funktionen erhalten Variablen als Input ggf. unter lokal neuem Namen
- Änderungen an den Input-Parametern wirken sich außerhalb der Funktion aus
Call by Value / Reference in C¶
- In C gibt es nur Call by Value
- Kann Call by Reference mittels Pointern realisieren
- Vektoren werden mit Call by Reference übergeben
- kein Widerspruch, Erklärung folgt gleich!
Call by Reference in C¶
- Elementare Datentypen werden in C mit
Call by Value an Funktionen übergeben
- z.B.
int,double, Pointer
- z.B.
Call by Reference ist über Pointer realisierbar:
Die Funktion
teständert den Wert der Variablex, da mittels Pointerydirekt auf den Speicher zugegriffen wird.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <stdio.h>
void test(int* y) {
printf("a) *y=%d\n", *y);
*y = 43;
printf("b) *y=%d\n", *y);
}
int main() {
int x = 12;
printf("c) x=%d\n", x);
test(&x);
printf("d) x=%d\n", x);
}
|
c) x=12 a) *y=12 b) *y=43 d) x=43
Beispiel¶
determineMinMaxsoll Minimum und Maximum eines Vektors finden- d.h. zwei Rückgabe-Parameter
- in C maximal ein Rückgabe-Parameter erlaubt
- Verwende Pointer für Call by Reference
- mehr als eine Funktionalität = schlechter Stil:
- jede Funktion hat genau eine Funktionalität
- jede Funktionalität erfordert eine Funktion
- oft trotzdem verwendet, weil effizienter:
- hier nur eine Schleife, statt zwei!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 | #include <stdio.h>
#include <assert.h>
#define DIM 5
// The function scanVector reads the coefficients
// of a double vector of length dim from the keyboard
void scanVector(double input[], int dim);
// The function determineMinMax returns the minimum
// and maximum of a double vector of length dim. We
// use Call-by-Reference because of 2 return values.
void determineMinMax(double vector[],int dim,
double* min, double* max);
int main() {
double x[DIM];
double max = 0;
double min = 0;
scanVector(x,DIM);
determineMinMax(x,DIM, &min, &max);
printf("min(x) = %f\n",min);
printf("max(x) = %f\n",max);
}
void scanVector(double input[], int dim) {
assert(dim > 0);
int j = 0;
for (j=0; j<dim; ++j) {
input[j] = 0;
printf("%d: ",j);
scanf("%lf",&input[j]);
}
}
void determineMinMax(double vector[],int dim,
double* min, double* max) {
int j = 0;
assert(dim > 0);
// First guess for minimum as well as maximum is the
// first vector coefficient.
// Recall that, e.g., max is double* so that *max is
// a double variable.
*max = vector[0];
*min = vector[0];
// iterate through vector and search for smaller resp.
// larger elements to determine minimum and maximum.
for (j=1; j<dim; ++j) {
if (vector[j] < *min) {
*min = vector[j];
}
else if (vector[j] > *max) {
*max = vector[j];
}
}
}
|
0: 4 1: 3 2: 5 3: 6 4: 7 min(x) = 3.000000 max(x) = 7.000000
Anmerkungen zu Pointern¶
Sind
int*,double*Datentypen?-Erfinder sagen Nein!
int *pointerdeklariert Pointer aufint- im Gegensatz zu:
pointerist vom Datentypint*
Verschiedene Sichtweisen sind beinahe äquivalent
Leerzeichen wird vom Compiler ignoriert:
int* pointer,int * pointer,int *pointer
*wird nur auf den folgenden Namen bezogenACHTUNG bei Deklaration von Listen:
int* pointer, var;deklariert Pointer aufintund Variable vom Typintint *pointer1, *pointer2;deklariert zwei Pointer aufint
ALSO Listen von Pointern vermeiden!
- auch zwecks Lesbarkeit!
Elementare Datentypen¶
Elementare Datentypen¶
Datentyp für Zeichen (z.B. Buchstaben)
char
Datentypen für Ganzzahlen:
int
Datentypen für Gleitkommazahlen:
float(einfach genaue Gleitk.zahlen, Single)double(doppelt genaue Gleitkommazahlen)
Alle Pointer gelten als elementare Datentypen
Qualifier (nicht in EPROG!)}
Qualifier (nicht in EPROG)¶
signedundunsignedfürcharundintlongundshortfürintlongfürdouble- z.B. Datentyp
signed char,unsigned long int - siehe https://en.wikipedia.org/wiki/C_data_types
- z.B. Datentyp
Bemerkungen¶
Deklaration und Gebrauch wie bisher
Man kann Arrays & Pointer bilden
Für UE: nur
char,int,doublePointerGenaueres zu den Typen später!
Funktionen¶
Elementare Datentypen werden an Funktionen mit Call by Value übergeben
Return Value darf nur
voidoder elementar sein
Arrays¶
Streng genommen, gibt es in C keine Arrays!
- Deklaration
int array[N];- legt Pointer
arrayvom Typint*an - organisiert ab der Adresse
arraySpeicher, umN-mal einenintzu speichern - d.h.
arrayenthält Adresse vonarray [0] - d.h.
array& array[0] - d.h.
*arrayarray[0] - Da Pointer als elementare Datentypen mittels Call by Value übergeben werden, werden Arrays augenscheinlich mit Call by Reference übergeben
- legt Pointer
- Deklaration
Pointerarithmetik:
array+j& array [j]- d.h.
*(array + j)array [j]
- d.h.
Laufzeitfehler!¶
- Ziel:
scanVectorsoll Vektor anlegen & initialisieren - Syntax des Programms ist OK, aber Laufzeitfehler!
- Problem: Speicher zu
xmit Blockende 14 aufgelöst- d.h. Pointer aus 6/13 zeigt auf Irgendwas
- Abhilfe: Call by Reference (vorher!) oder händische Speicherverwaltung (gleich!)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | #include <stdio.h>
#include <assert.h>
double* scanVector(int length) {
assert(length > 0);
double vector[length];
int j = 0;
for (j=0; j<length; ++j) {
vector[j] = 0;
printf("vector[%d] = ",j);
scanf("%lf",&vector[j]);
}
return vector;
}
int main() {
double* x;
int j = 0;
int dim = 0;
printf("dim = ");
scanf("%d",&dim);
x = scanVector(dim);
for (j=0; j<dim; ++j) {
printf("x[%d] = %f\n",j,x[j]);
}
}
|
/tmp/tmpw5npq09t.c: In function ‘scanVector’:
/tmp/tmpw5npq09t.c:13:10: warning: function returns address of local variable [-Wreturn-local-addr]
13 | return vector;
| ^~~~~~
dim = 4 vector[0] = 3 vector[1] = 4 vector[2] = 5 vector[3] = 6
[C kernel] Executable exited with code -11
Der Befehl sizeof¶
- Ist
vareine Variable eines elementaren Datentyps, gibtsizeof(var)die Größe der Var. in Bytes zurück - Ist
typeein Datentyp, so gibtsizeof(type)die Größe einer Variable dieses Typs in Bytes zurück - Ist
arraylokales statisches Array im selben Block, so liefertsizeof(array)Größe des Arrays in Bytes - Intern sind
ptrundarrayzweidoublePointer und enthalten (= zeigen auf) dieselbe Speicheradresse!
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | #include <stdio.h>
void printSizeOf(double vector[]) {
printf("sizeof(vector) = %d\n",sizeof(vector));
}
int main() {
int var = 43;
double array[12];
double* ptr = array;
printf("sizeof(var) = %d\n",sizeof(var));
printf("sizeof(double) = %d\n",sizeof(double));
printf("sizeof(array) = %d\n",sizeof(array));
printf("sizeof(ptr) = %d\n",sizeof(ptr));
printSizeOf(array);
}
|
/tmp/tmp644_iya1.c: In function ‘printSizeOf’:
/tmp/tmp644_iya1.c:4:40: warning: ‘sizeof’ on array function parameter ‘vector’ will return size of ‘double *’ [-Wsizeof-array-argument]
4 | printf("sizeof(vector) = %d\n",sizeof(vector));
| ^
/tmp/tmp644_iya1.c:3:25: note: declared here
3 | void printSizeOf(double vector[]) {
| ~~~~~~~^~~~~~~~
sizeof(var) = 4 sizeof(double) = 8 sizeof(array) = 96 sizeof(ptr) = 8 sizeof(vector) = 8
Dynamische Speicherverwaltung¶
Statische Arrays¶
double array[N];deklariert statischen Vektorarrayder LängeNmitdouble-Komponenten- Indizierung
array[j]mit arrayist intern vom Typdouble*- enthält Adr. von
array[0], sog. Base Pointer
- enthält Adr. von
- Länge
Nkann während Programmablauf nicht verändert werden
- Indizierung
Speicher des Arrays wird mit Blockende aufgelöst, d.h., kann keine statischen Arrays in Funktionen anlegen und zurückgeben (siehe letztes Beispiel)
Speicher allokieren¶
Jetzt: händische Speicherverwaltung von Arrays
- dadurch Vektoren dynamischer Länge möglich
- Speicher wird erst durch expliziten Befehl aufgelöst
Einbinden der Standard-Bibl:
#include <stdlib.h>- 3 neue Befehle:
malloc,free,realloc - neue Konstante:
NULL
- 3 neue Befehle:
pointer = malloc(N*sizeof(type));- allokiert Speicher für Vektor der Länge
Nmit Komponenten vom Typtypemallockriegt Angabe in Bytessizeof
pointermuss vom Typtype*sein- Base Pointer
pointerbekommt Adresse der ersten Komponentepointer[0]
- Base Pointer
pointerundNmuss sich Programm merken!
- allokiert Speicher für Vektor der Länge
Häufiger Laufzeitfehler:
sizeofvergessen!Achtung: Allokierter Speicher ist uninitialisiert!
Konvention: Pointer ohne Speicher bekommen den Wert
NULLzugewiesen- führt sofort auf Speicherzugriffsfehler bei Zugriff
mallocliefertNULL, falls Fehler bei Allokation- d.h. Speicher konnte nicht allokiert werden
Speicher freigeben¶
free(pointer)- gibt Speicher eines dyn. Vektors frei
pointermuss Output vonmallocsein
Achtung: Speicher wird freigegeben, aber
pointerexistiert weiter- Erneuter Zugriff führt (irgendwann) auf Laufzeitfehler
Achtung: Speicher freigeben, nicht vergessen!
- und Pointer auf
NULLsetzen!
- und Pointer auf
Beispiel¶
Ziel:
scanVectorsoll Vektor anlegen & einlesen- Vergleiche Beispiel mit statischen Vektoren
Jetzt aber Code OK, da Funktion den Vektor dynamisch mit
mallocallokiert- Vektor existiert (d.h. Speicher ist reserviert),
bis Basepointer mit
freefreigegeben!
- Vektor existiert (d.h. Speicher ist reserviert),
bis Basepointer mit
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 | #include <stdio.h>
#include <stdlib.h>
#include <assert.h>
// scanVector allocates a double vector of prescribed
// length and reads the coefficients from the keyboard
double* scanVector(int length) {
int j = 0;
double* vector = NULL;
// ensure that given length is admissible
assert(length > 0);
// allocate memory and ensure that this was successful
vector = malloc(length*sizeof(double));
assert(vector != NULL);
// read coefficients from keyboard
for (j=0; j<length; ++j) {
vector[j] = 0;
printf("vector[%d] = ",j);
scanf("%lf",&vector[j]);
}
// return base pointer of dynamic vector
return vector;
}
// printVector prints vector of given length in the shell
void printVector(double* vector, int length) {
int j = 0;
// ensure that vector and length are admissible
assert(vector != NULL);
assert(length > 0);
// print coefficients to shell
for (j=0; j<length; ++j) {
printf("vector[%d] = %f\n",j,vector[j]);
}
}
int main() {
// always set pointers to NULL, if not bound to memory
double* x = NULL;
int dim = 0;
// read vector length from keyboard
printf("dim = ");
scanf("%d",&dim);
// allocate vector, read coefficients, and print vector
x = scanVector(dim);
printVector(x,dim);
// do not forget to free memory
free(x);
// set pointer x to NULL, since not bound to memory
x = NULL;
}
|
dim = 4 vector[0] = 1 vector[1] = 2 vector[2] = 3 vector[3] = 4 vector[0] = 1.000000 vector[1] = 2.000000 vector[2] = 3.000000 vector[3] = 4.000000
Dynamische Vektoren¶
pointer = realloc(pointer, Nnew*sizeof(type))- verändert Speicherallokation
- zusätzliche Allokation für
Nnew > N - Speicherbereich kürzen für
Nnew < N
- zusätzliche Allokation für
- Alter Inhalt bleibt (soweit möglich) erhalten
- Rückgabe
NULLbei Fehler
- verändert Speicherallokation
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | #include <stdio.h>
#include <stdlib.h>
#include <assert.h>
int main() {
int N = 5;
int Nnew = 10;
int j = 0;
int* array = malloc(N*sizeof(int));
assert(array != NULL);
for (j=0; j<N; ++j){
array[j] = j;
}
array = realloc(array,Nnew*sizeof(int));
assert(array != NULL);
for (j=N; j<Nnew; ++j){
array[j] = 10*j;
}
for (j=0; j<Nnew; ++j){
printf("%d ",array[j]);
}
printf("\n");
free(array);
array = NULL;
}
|
0 1 2 3 4 50 60 70 80 90
Bemerkungen¶
- Base Pointer (= Output von
mallocbzw.realloc) merken & nicht verändern- notwendig für fehlerfreies
freeundrealloc
- notwendig für fehlerfreies
- bei
mallocundreallocnichtsizeofvergessen- Typ des Base Pointers muss zum
sizeofpassen!
- Typ des Base Pointers muss zum
- Output von
mallocundreallocaufNULLchecken- sicherstellen, dass Speicher allokiert wurde!
- allokierter Speicherbereich ist stets uninitialisiert
- nach Allokation stets initialisieren
- Länge des dynamischen Arrays merken
- kann Programm nicht herausfinden!
- Nicht mehr benötigten Speicher freigeben
- insb. vor Blockende
...}, da dann Base Pointer weg
- insb. vor Blockende
- Pointer auf
NULLsetzen, wenn ohne Speicher- Fehlermeldung, falls Programm "aus Versehen"
auf Komponente
array[j]zugreift
- Fehlermeldung, falls Programm "aus Versehen"
auf Komponente
- Nie
realloc,freeauf statisches Array anwenden- Führt auf Laufzeitfehler, da Compiler
freeselbständig hinzugefügt hat!
- Führt auf Laufzeitfehler, da Compiler
- Ansonsten gleicher Zugriff auf Komponenten wie
bei statischen Arrays
- Indizierung
array[j]für
- Indizierung
Anwendung für Pointer: Eine Vektor Bibliothek¶
Aufteilen von Source-Code¶
längere Source-Codes auf mehrere Files aufteilen
Vorteil:
- übersichtlicher
- Bildung von Bibliotheken
- Wiederverwendung von alten Codes
- vermeidet Fehler
gcc name1.c name2.c ...- erstellt ein Executable aus Source-Codes
- Reihenfolge der Codes nicht wichtig
- analog zu
gcc all .c- wenn
all .cganzen Source-Code enthält
- wenn
- insb. Funktionsnamen müssen eindeutig sein
main()darf nur 1x vorkommen
Preprocessor, Compiler & Linker¶
Beim Kompilieren von Source-Code werden mehrere Stufen durchlaufen:
- Preprocessor-Befehle ausführen, z.B.
#include - Compiler erstellt Objekt-Code
- Objekt-Code aus Bibliotheken wird hinzugefügt
- Linker ersetzt symbolische Namen im Objekt-Code durch Adressen und erzeugt Executable
- Preprocessor-Befehle ausführen, z.B.
Bibliotheken = vorkompilierter Objekt-Code
- plus zugehöriges Header-File
Standard-Linker in Unix ist
ldNur Schritt (3) fertig, d.h. Objekt-Code erzeugen
gcc -c name .cerzeugt Objekt-Codename .o- gut zum Debuggen von Syntax-Fehlern!
Objekt-Code händisch hinzufügen + kompilieren
gcc name.c bib1.o bib2.o ...gcc name.o bib1.o bib2.o ...- Reihenfolge + Anzahl der Objekt-Codes ist egal
- Ziel: selbst Bibliotheken erstellen
- spart ggf. Zeit beim Kompilieren
- vermeidet Fehler
Eine erste Bibliothek¶
- Header-File
dynamicvectors.hzur Bibliothek- enthält alle Funktionssignaturen
- enthält Kommentare zu den Funktionen
- sog. Include Guard: Header-File beginnt mit
#ifndef NAME#define NAME Header-File ended mit
#endifkeine erneute Deklaration bei mehrfachen
#include
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | #ifndef INCLUDE_DYNAMICVECTORS__
#define INCLUDE_DYNAMICVECTORS__
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
// allocate + initialize dynamic double vector of length n
double* mallocVector(int n);
// free a dynamic vector and set the pointer to NULL
double* freeVector(double* vector);
// extend dynamic double vector and initialize new entries
double* reallocVector(double* vector, int n, int nnew);
// allocate dynamic double vector of length n and read
// entries from keyboard
double* scanVector(int n);
// print dynamic double vector of length n to shell
void printVector(double* vector, int n);
#endif
|
Source-Code¶
- Einbinden des Header-Files (Zeile 1)
#include "..."mit Angabe des Verzeichnis#include <...>für Standard-Verzeichnis
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 | #include "dynamicvectors.h"
double* mallocVector(int n) {
int j = 0;
double* vector = NULL;
assert(n > 0);
vector = malloc(n*sizeof(double));
assert(vector != NULL);
for (j=0; j<n; ++j) {
vector[j] = 0;
}
return vector;
}
double* freeVector(double* vector) {
free(vector);
return NULL;
}
double* reallocVector(double* vector, int n, int nnew) {
int j = 0;
assert(vector != NULL);
assert(n > 0);
assert(nnew > 0);
vector = realloc(vector,nnew*sizeof(double));
assert(vector != NULL);
for (j=n; j<nnew; ++j) {
vector[j] = 0;
}
return vector;
}
double* scanVector(int n) {
int j = 0;
double* vector = NULL;
assert(n > 0);
vector = mallocVector(n);
assert(vector != NULL);
for (j=0; j<n; ++j) {
printf("vector[%d] = ",j);
scanf("%lf",&vector[j]);
}
return vector;
}
void printVector(double* vector, int n) {
int j = 0;
assert(vector != NULL);
assert(n > 0);
for (j=0; j<n; ++j) {
printf("%d: %f\n",j,vector[j]);
}
}
|
Hauptprogramm¶
- Hauptprogramm bindet Header der Bibliothek ein
- Kompilieren mittels
gcc -c dynamicvectors.c- erzeugt Object-Code
dynamicvectors.o
- erzeugt Object-Code
gcc dynamicvectors_main .c dynamicvectors.o- erzeugt Executable
a.out
- erzeugt Executable
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | //%cflags:data/dynamicvectors.o -I data/
//ACHTUNG: Zeile 1 ist nur fuer die korrekte Funktion des interaktiven
// Skriptums noetig (ersetzt gcc ... dynamicvectors.o)
#include "dynamicvectors.h"
int main() {
double* x = NULL;
int n = 10;
int j = 0;
x = mallocVector(n);
for (j=0; j<n; ++j) {
x[j] = j;
}
x = reallocVector(x,n,2*n);
for (j=n; j<2*n; ++j) {
x[j] = 10*j;
}
printVector(x,2*n);
x = freeVector(x);
}
|
0: 0.000000 1: 1.000000 2: 2.000000 3: 3.000000 4: 4.000000 5: 5.000000 6: 6.000000 7: 7.000000 8: 8.000000 9: 9.000000 10: 100.000000 11: 110.000000 12: 120.000000 13: 130.000000 14: 140.000000 15: 150.000000 16: 160.000000 17: 170.000000 18: 180.000000 19: 190.000000
Strings¶
Strings (= Zeichenketten)¶
- Strings =
char-Arrays, also 2 Definitionen möglich- statisch:
char array[N];- N = statische Länge
- Deklaration & Initialisierung möglich
char array[] = "text";
- dynamisch (wie oben, Typ: char*)
- statisch:
- Fixe Strings in Anführungszeichen
"..." - Einzelnes Zeichen in Hochkommata
'.' - Zugriff auf Teil-Strings nicht möglich!
Achtung bei dynamischen Strings:
- als Standard enden alle Strings
mit Null-Byte
\0- kann Länge eines Strings dadurch bestimmen!
- Bei statischen Arrays geschieht das automatisch
(also wirkliche Länge
N+1undarray[N] ='\0') - Bei dyn. Strings also 1 Byte mehr reservieren!
- und
\0nicht vergessen
- als Standard enden alle Strings
mit Null-Byte
An Funktionen können auch fixe Strings (in Anführungszeichen) übergeben werden
- z.B.
printf("Hello World!\n");
- z.B.
Funktionen zur String-Manipulation¶
Wichtigste Funktionen in
stdio.hsprintf/sscanfagieren wieprintf/scanf, aber Output / Input = String
zahreiche Funktionen in
stdlib.h, z.B.atof: konvertiert Stringdoubleatoi: konvertiert Stringint
oder in
string.h, z.B.strchr,memchr: Suchecharinnerhalb Stringstrcmp,memcmp: Vergleiche zwei Stringsstrcpy,memcpy: Kopieren von Stringsstrlen: Länge eines Strings (ohne Null-Byte)
Header-Files mit
#include <name>einbinden!Gute Referenz mit allen Befehlen & Erklärungen
Details zu den Befehlen in UNIX mit
man 3 befehl- sog. UNIX programmer's manual
- z.B. Eingabe
man 3 strcpyin der Shell
ACHTUNG mit String-Befehlen: Befehle können nicht wissen, ob für den Output-String genügend Speicher allokiert ist ( Laufzeitfehler!)
Beispiel¶
Fixe Strings in Anführungszeichen
"..."(Zeile 21)- erzeugt statisches Array mit zusätzlichem Null-Byte am Ende
Zugriff auf einzelnes Zeichen eines Strings mit einfachen Hochkommata
'.'(Zeile 23)Platzhalter für Strings in
printfist%s(Zeile 24)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | #include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <assert.h>
char* stringCopy(char* source) {
int length = 0;
char* result = NULL;
// ensure that source string exists
assert(source != NULL);
// determine length and allocate memory
length = strlen(source);
result = malloc((length+1)*sizeof(char));
// copy source string and return copy
strcpy(result,source);
return result;
}
int main() {
char* string1 = "Hello World?";
char* string2 = stringCopy(string1);
string2[11] = '!';
printf("%s %s\n",string1,string2);
free(string2);
string2=NULL;
}
|
Hello World? Hello World!
Funktionspointer¶
Funktionspointer¶
Funktionsaufruf ist Sprung an eine Adresse
- Pointer speichern Adressen
- kann daher Fkt-Aufruf mit Pointer realisieren
Deklaration eines Funktionspointers:
<return value>(*pointer)(<input>);deklariert Pointerpointerfür Funktionen mit Parametern<input>und Ergebnis vom Typ<return value>- Notation entpricht der C-Denkweise:
- Was bekommt man, wenn man
pointerdereferenziert? Funktionfctmit Signatur<return value>fct(<input>)
- Was bekommt man, wenn man
Bei Zuweisung müssen Pointer
pointerund Funktion denselben Aufbau haben- gleicher Return-Value
- gleiche Input-Parameter-Liste
- Aufruf einer Funktion über Pointer wie bei normalem Funktionsaufruf!
Elementares Beispiel¶
- Deklaration eines Funktionspointers in Zeile 13
- Zuweisung auf Fkt.pointer in Zeile 16 + 20
- Fkt.aufruf über Pointer in Zeile 17 + 21
- Achtung: kein dereferenzieren notwendig
(*output)(string)ist gleichoutput(string)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | #include <stdio.h>
void output1(char* string) {
printf("*%s*\n",string);
}
void output2(char* string) {
printf("#%s#\n",string);
}
int main() {
char string[] = "Hello World";
void (*output)(char* string) = NULL;
// call function output1 via function pointer
output = output1;
output(string);
// call function output2 via function pointer
output = output2;
output(string);
}
|
*Hello World* #Hello World#
Beispiel: Bisektionsverfahren (schon wieder)¶
- Approximation der Nullstelle von
auf dem Intervall auf Genauigkeit
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 | #include <stdio.h>
#include <assert.h>
#include <math.h>
// bisection returns an approximate root x0 of a
// continuous real-valued scalar function fct with
// fct(a) * fct(b) <= 0, for which the intermediate
// value theorem yields the existence of a root.
//
// bisection takes the function pointer of the function
// fct: [a,b] -> R and a tolerance tol and returns x0
// in (a,b) such that |x0 - x| <= tol, where fct(x) = 0.
double bisection(double (*fct)(double x),
double a, double b, double tol);
// demo function f
double f(double x) {
return x*x + exp(x) - 2;
}
int main() {
double a = 0;
double b = 10;
double tol = 1e-12;
double x = bisection(f,a,b,tol);
printf("Approximate zero of the function x=%1.15e\n",x);
}
double bisection(double (*fct)(double x),
double a, double b, double tol) {
double m = 0;
double fa = 0;
double fm = 0;
// ensure that input is admissible
assert(a < b);
fa = fct(a);
assert(fa*fct(b) <= 0);
// iterate by interval bisection
while ( b-a > 2*tol) {
// compute interval mitpoint and evaluate fct
m = (a+b)/2;
fm = fct(m);
if ( fa*fm <= 0 ) {
// theorem guarantees root in [a,m]
b = m;
}
else {
// theorem guarantees root in [m,b]
a = m;
fa = fm;
}
}
// as loop terminates, x in [a,b] and |b-a| <= 2*tol
// so that |x-m| <= tol for the midpoint m.
return m;
}
|
Approximate zero of the function x=5.372744491739923e-01
Strukturen¶
Deklaration von Strukturen¶
- Funktionen
- Zusammenfassung von verschiedenen Befehlen, um Abstraktionsebenen zu schaffen
Strukturen
- Zusammenfassung von Variablen verschiedener Datentypen zu einem neuen Datentyp
- Abstraktionsebenen bei Daten
Beispiel: Verwaltung der EPROG-Teilnehmer
- pro Student jeweils denselben Datensatz
Semikolon nach Struktur-Deklarations-Block
- erzeugt neuen Variablen-Typ
Student
1 2 3 4 5 6 7 8 9 10 | // declaration of structure and corresponding data type
typedef struct _Student_ {
char* firstname;
char* lastname;
int studentID;
int studiesID;
double final_test;
double kreuzerl;
double exercise;
} Student;
|
Strukturen & Members¶
- Datentypen einer Struktur heißen Members
- Zugriff auf Members mit Punkt-Operator
varVariable vom TypStudent- z.B. Member
var.firstname
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | // declaration of structure
struct _Student_ {
char* firstname; // first name
char* lastname; // last name
int studentID; // student ID
int studiesID; // studies ID
double final_test; // points in final test
double kreuzerl; // percentage of Kreuzerl
double exercise; // points in exercises
};
// declaration of corresponding data type
typedef struct _Student_ Student;
main() {
// declaration of variable var of type Student
Student var;
// assign values to members of struct variable
var.firstname = "Dirk";
var.lastname = "Praetorius";
var.studentID = 0;
var.studiesID = 680;
var.final_test = 25.;
var.kreuzerl = 0.7;
var.exercise = 35.;
}
|
Kombinierte Deklaration¶
- gleichzeitige Deklaration von
structundtypedef - anstelle von
struct _Student_ { ... }; typedef struct _Student_ Student; - einfach
typedef struct _Student_{ ... } Student;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | // declaration of structure and corresponding data type
typedef struct _Student_ {
char* firstname;
char* lastname;
int studentID;
int studiesID;
double final_test;
double kreuzerl;
double exercise;
} Student;
main() {
// declaration of variable var of type Student
Student var;
// assign values to members of struct variable
var.firstname = "Dirk";
var.lastname = "Praetorius";
var.studentID = 0;
var.studiesID = 680;
var.final_test = 25.;
var.kreuzerl = 0.7;
var.exercise = 35.;
}
|
Bemerkungen zu Strukturen¶
laut erstem C-Standard verboten:
- Struktur als Input-Parameter einer Funktion
- Struktur als Output-Parameter einer Funktion
- Zuweisungsoperator (
=) für gesamte Struktur
in der Zwischenzeit erlaubt, aber trotzdem:
- idR. Strukturen dynamisch über Pointer
- Zuweisung (= Kopieren) selbst schreiben
- Zuweisung (
=) macht sog. shallow copy
Shallow copy:
- nur die oberste Ebene wird kopiert
- d.h. Werte bei elementaren Variablen
- d.h. Adressen bei Pointern
- also: Kopie hat (physisch!) dieselben dynamischen Daten
Deep copy:
- alle Ebenen der Struktur werden kopiert
- d.h. alle Werte bei elementaren Variablen
- plus Kopie der dynamischen Inhalte (d.h. durch Pointer adressierter Speicher)
Strukturen: Speicher allokieren¶
- Also Funktionen anlegen
newStudent: Allokieren und InitialisierenfreeStudent: Freigeben des SpeicherscloneStudent: Vollständige Kopie der Struktur inkl. dyn. Felder, z.B. Memberfirstname(sog. deep copy)copyStudent: Kopie der obersten Ebene exkl. dynamischer Felder (sog. shallow copy)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | Student* newStudent() {
// allocate memory for struct variable as before.
// Do not forget to use sizeof within malloc!
Student* pointer = malloc(sizeof(Student));
assert( pointer != NULL);
// dereferencing of the pointer yields a struct variable
// of type Student. The use of brackets is mandatory!
(*pointer).firstname = NULL;
(*pointer).lastname = NULL;
(*pointer).studentID = 0;
(*pointer).studiesID = 0;
(*pointer).final_test = 0.;
(*pointer).kreuzerl = 0.;
(*pointer).exercise = 0.;
return pointer;
}
|
Strukturen & Pfeiloperator¶
- Im Programm ist
pointervom TypStudent* - Zugriff auf Members, z.B.
(*pointer).firstname- Bessere Schreibweise dafür
pointer->firstname
- Bessere Schreibweise dafür
- Strukturen nie statisch, sondern stets
dynamisch
- Verwende gleich
studentfür TypStudent*
- Verwende gleich
- Funktion
newStudentlautet besser wie folgt
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | // declaration of structure and corresponding data type
typedef struct _Student_ {
char* firstname;
char* lastname;
int studentID;
int studiesID;
double final_test;
double kreuzerl;
double exercise;
} Student;
// allocate and initialize new student
Student* newStudent() {
Student* student = malloc(sizeof(Student));
assert(student != NULL);
student->firstname = NULL;
student->lastname = NULL;
student->studentID = 0;
student->studiesID = 0;
student->final_test = 0.;
student->kreuzerl = 0.;
student->exercise = 0.;
return student;
}
|
Strukturen: Speicher freigeben¶
- Freigeben einer dynamisch erzeugten
Struktur-Variable vom Typ
Student - Achtung: Zugewiesenen dynamischen Speicher
vor Freigabe des Strukturpointers freigeben
- hier:
firstname,lastname - alle anderen Members sind elementar
- hier:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | // free memory allocation
Student* delStudent(Student* student) {
assert(student != NULL);
// delete firstname, if memory has been allocated
if (student->firstname != NULL) {
free(student->firstname);
}
// delete lastname, if memory has been allocated
if (student->lastname != NULL) {
free(student->lastname);
}
// delete memory of struct variable and return NULL
free(student);
return NULL;
}
|
Shallow Copy¶
- Kopieren einer dynamisch erzeugten
Struktur-Variable vom Typ
Student- Kopieren der obersten Ebene einer Struktur exklusive dynamischen Speicher (Members!)
- ACHTUNG: Original und Shallow-Kopie teilen sich die dynamischen Felder
- d.h. physisch derselbe
firstnameundlastname - Änderung
firstnamevom Original ändert auchfirstnameder Shallow-Kopie- Anwendung von
freeStudentauf Kopie und Shallow-Kopie liefert Laufzeitfehler
- Anwendung von
- Nach erstem Aufruf ist bereits Speicher von
firstnameundlastnamefreigegeben
- d.h. physisch derselbe
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | // shallow copy of student
Student* copyStudent(Student* student) {
Student* copy = newStudent();
assert(student != NULL);
// note: for pointes, only adresses are copied
copy->firstname = student->firstname;
copy->lastname = student->lastname;
// copy of elementary data
copy->studentID = student->studentID;
copy->studiesID = student->studiesID;
copy->final_test = student->final_test;
copy->kreuzerl = student->kreuzerl;
copy->exercise = student->exercise;
return copy;
}
|
Deep Copy¶
- Kopieren einer dynamisch erzeugten
Struktur-Variable vom Typ
Student - Vollständige Kopie, inkl. dynamischem Speicher
- Achtung: Zugewiesenen dynamischen Speicher mitkopieren
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | // deep copy of student
Student* cloneStudent(Student* student) {
Student* copy = newStudent();
int length = 0;
assert( student != NULL);
// full copy of firstname
if (student->firstname != NULL) {
length = strlen(student->firstname);
copy->firstname = malloc((length+1)*sizeof(char));
assert(copy->firstname != NULL);
strcpy(copy->firstname, student->firstname);
}
// full copy of lastname
if (student->lastname != NULL) {
length = strlen(student->lastname);
copy->lastname = malloc((length+1)*sizeof(char));
assert(copy->lastname != NULL);
strcpy(copy->lastname, student->lastname);
}
// copy of elementary data
copy->studentID = student->studentID;
copy->studiesID = student->studiesID;
copy->final_test = student->final_test;
copy->kreuzerl = student->kreuzerl;
copy->exercise = student->exercise;
return copy;
}
|
Arrays von Strukturen¶
- Ziel: Array mit Teilnehmern von EPROG erstellen
- keine statischen Arrays verwenden,
sondern dynamische Arrays
- Studenten-Daten sind vom Typ
Student - also intern verwaltet mittels Typ
Student* - also Array vom Typ
Student**
- Studenten-Daten sind vom Typ
- Zugriff auf Members wie vorher
participant[j]ist vom TypStudent*- also z.B.
participant[j]->firstname
1 2 3 4 5 6 7 | // declare array
Student** participant = malloc(N*sizeof(Student*));
// allocate memory for participants
for (j=0; j<N; ++j){
participant[j] = newStudent();
}
|
Schachtelung von Strukturen¶
Mitarbeiterdaten strukturieren
- Name, Wohnadresse, Büroadresse
Für
employeevom TypEmployee*employee->homePointer aufAddress- also z.B.
employee->home->city
- Achtung beim Allokieren, Freigeben, Kopieren
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | typedef struct _Address_ {
char* street;
char* number;
char* city;
char* zip;
} Address;
typedef struct _Employee_ {
char* firstname;
char* lastname;
char* title;
Address* home;
Address* office;
} Employee;
|
Strukturen & Mathematik¶
Abstand zweier Punkte im ¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 | #include <stdlib.h>
#include <stdio.h>
#include <assert.h>
#include <math.h>
typedef struct _Vector3_ {
double x;
double y;
double z;
} Vector3;
Vector3* newVector3(double x, double y, double z) {
Vector3* v = malloc(sizeof(Vector3));
assert(v != NULL); // ensure proper memory allocation
v->x = x;
v->y = y;
v->z = z;
return v;
}
Vector3* delVector3(Vector3* v) {
assert(v != NULL); // ensure that vector v exists
free(v);
return NULL;
}
double dist(Vector3* v, Vector3* w) {
assert(v != NULL); // ensure that vector v exists
assert(w != NULL); // ensure that vector w exists
return sqrt( (v->x - w->x)*(v->x - w->x)
+ (v->y - w->y)*(v->y - w->y)
+ (v->z - w->z)*(v->z - w->z) );
}
int main() {
Vector3* v = newVector3(1,1,1);
Vector3* w = newVector3(1,2,3);
printf("dist(x,y) = %f\n", dist(v,w));
v = delVector3(v);
w = delVector3(w);
}
|
dist(x,y) = 2.236068
Strukturen und Vektoren¶
- Datentyp zur Speicherung von
- Dimension vom Typ
int - Datenfeld zur Speicherung von
double
- Dimension vom Typ
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | #ifndef INCLUDE_VECTOR__
#define INCLUDE_VECTOR__
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <math.h>
// declaration of new data type Vector
typedef struct _Vector_ {
int n; // Dimension
double* entry; // Vector coefficients
} Vector;
// allocate and initialize new vector of length n
Vector* newVector(int n);
// free storage of allocated vector and return NULL
Vector* delVector(Vector* X);
// return length of a vector
int getVectorN(Vector* X);
// return coefficient Xi of vector X
double getVectorEntry(Vector* X, int i);
// assign new value to coefficient Xi of vector X
void setVectorEntry(Vector* X, int i, double Xi);
// some example functions...
Vector* inputVector();
double normVector(Vector* X);
double productVector(Vector* X, Vector* Y);
#endif
|
Allokieren eines Vektors¶
- Funktion bekommt Länge des Vektors
- allokiert Struktur, weist Dimension zu
- allokiert und initialisiert Datenfeld
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | Vector* newVector(int n) {
int i = 0;
Vector* X = NULL;
assert(n > 0);
X = malloc(sizeof(Vector));
assert(X != NULL);
X->n = n;
X->entry = malloc(n*sizeof(double));
assert(X->entry != NULL);
for (i=0; i<n; ++i) {
X->entry[i] = 0;
}
return X;
}
|
Freigeben eines Vektors¶
- Datenfeld freigeben
- Struktur freigeben
NULLzurückgeben
1 2 3 4 5 6 7 | Vector* delVector(Vector* X) {
assert(X != NULL);
free(X->entry);
free(X);
return NULL;
}
|
Zugriff auf Strukturen¶
- Es ist guter (aber seltener) Programmierstil, auf Members einer Struktur nicht direkt zuzugreifen
- Stattdessen lieber für jeden Member
setundgetschreiben- Wenn kein
set, dann Schreiben nicht erlaubt! - Wenn kein
get, dann Lesen nicht erlaubt!
- Wenn kein
- Dieses Vorgehen erlaubt leichte Umstellung der Datenstruktur bei späteren Modifikationen
- Dieses Vorgehen vermeidet Inkonsistenzen der Daten und insbesondere Laufzeitfehler
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | int getVectorN(Vector* X) {
assert(X != NULL);
return X->n;
}
double getVectorEntry(Vector* X, int i) {
assert(X != NULL);
assert((i >= 0) && (i < X->n));
return X->entry[i];
}
void setVectorEntry(Vector* X, int i, double Xi){
assert(X != NULL);
assert((i >= 0) && (i < X->n));
X->entry[i] = Xi;
}
|
Beispiel: Vektor einlesen¶
- Einlesen von und eines Vektors
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | Vector* inputVector() {
Vector* X = NULL;
int i = 0;
int n = 0;
double input = 0;
printf("Length of the vector n=");
scanf("%d",&n);
assert(n > 0);
X = newVector(n);
assert(X != NULL);
for (i=0; i<n; ++i) {
input = 0;
printf("x[%d]=",i);
scanf("%lf",&input);
setVectorEntry(X,i,input);
}
return X;
}
|
Beispiel: Euklidische Norm¶
- Berechne für
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | double normVector(Vector* X) {
double Xi = 0;
double norm = 0;
int n = 0;
int i = 0;
assert(X != NULL);
n = getVectorN(X);
for (i=0; i<n; ++i) {
Xi = getVectorEntry(X,i);
norm = norm + Xi*Xi;
}
norm = sqrt(norm);
return norm;
}
|
Beispiel: Skalarprodukt¶
- Berechne für
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | double productVector(Vector* X, Vector* Y) {
double Xi = 0;
double Yi = 0;
double product = 0;
int n = 0;
int i = 0;
assert(X != NULL);
assert(Y != NULL);
n = getVectorN(X);
assert(n == getVectorN(Y));
for (i=0; i<n; ++i) {
Xi = getVectorEntry(X,i);
Yi = getVectorEntry(Y,i);
product = product + Xi*Yi;
}
return product;
}
|
Zahldarstellung im Computer¶
Speichereinheiten¶
- 1 Bit = 1 b = kleinste Einheit, speichert oder
- 1 Byte = 1 B = Zusammenfassung von 8 Bit
- 1 Kilobyte = 1 KB = 1024 Byte
- nächste 2er Potenz an
- 1 Megabyte = 1 MB = 1024 KB
- 1 Gigabyte = 1 GB = 1024 MB
- 1 Terabyte = 1 TB = 1024 GB
Speicherung von Zahlen¶
- Zur Speicherung von Zahlen wird je nach Datentyp fixe Anzahl an Bytes verwendet
- Konsequenz:
- pro Datentyp gibt es nur endlich viele Zahlen
- d.h. es gibt jeweils größte und kleinste Zahl!
Ganzzahlen¶
- Mit Bits kann man Ganzzahlen darstellen
- Standardmäßig betrachtet man
- entweder alle ganzen Zahlen in
- oder alle ganzen Zahlen in
Integer-Arithmetik¶
exakte Arithmetik innerhalb
Überlauf: Ergebnis von Rechnung
Unterlauf: Ergebnis von Rechnung
Integer-Arithmetik ist i.d.R. Modulo-Arithmetik
- d.h. Zahlenbereich ist geschlossen
- liefert
- liefert
- nicht im C-Standard festgelegt!
- d.h. Zahlenbereich ist geschlossen
Beispiel: unsigned 4-bit Integer¶
- 4 Speicherplätze für 0/1 16 verschiedene Zahlen ()
Formel:
a_3 a_2 a_1 a_0mit0 0 0 00 0 0 10 0 1 00 0 1 11 0 0 01 1 1 1
Addition wie im 10er System (mit Übertrag falls Ergebnis )
0 0 0 1+0 1 0 1=0 1 1 0()
Beispiel: 4-bit Integer¶
4 Speicherplätze für 0/1 16 verschiedene Zahlen ()
0 0 0 00 1 1 1
Beobachtung:
0 1 1 1+1 0 0 1=0 0 0 0( Übertrag bleibt übrig)- daher:
1 0 0 1 1 0 0 01 1 1 1
- daher:
- Daher:
0 1 1 1+0 0 0 1=1 0 0 0(Überlauf )
Beispiel: Integer in C¶
1 2 3 4 5 6 7 8 9 10 11 12 13 | #include <stdio.h>
int main() {
int j = 0;
int n = 8*sizeof(int); // number bits per int
int min = 1;
// compute 2^(n-1)
for (j=1; j<n; ++j) {
min = 2*min;
}
printf("n=%d, min=%d, max=%d\n",n,min,min-1);
}
|
n=32, min=-2147483648, max=2147483647
2 Milliarden sind nicht viel!¶
- Achtung: Millarden
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <stdio.h>
int main() {
int n = 1;
int factorial = 1;
do {
++n;
factorial = n*factorial;
printf("n=%d, n!=%d\n",n,factorial);
} while (factorial < n*factorial);
printf("n=%d, n!>%d\n",n+1,n*factorial);
}
|
n=2, n!=2 n=3, n!=6 n=4, n!=24 n=5, n!=120 n=6, n!=720 n=7, n!=5040 n=8, n!=40320 n=9, n!=362880 n=10, n!=3628800 n=11, n!=39916800 n=12, n!=479001600 n=13, n!=1932053504 n=14, n!>-653108224
Variablentypen short, int, long¶
Bits Ganzzahlen
In C sind
short,int,longmit Vorzeichen- d.h. ganze Zahlen in
Ganzzahlen durch zusätzliches
unsigned- d.h. ganze Zahlen in
- z.B.
unsigned int var1 = 0;
- Es gilt stets
shortintlonglong long- Standardlängen:
- 2 Byte (
short) - 4 Byte (
int) - 8 Byte (
long long, seit C99)
- 2 Byte (
- In der Regel gilt
int=long
- Standardlängen:
- https://en.wikipedia.org/wiki/C_data_types
- Für die UE nur
intverwenden
Variablentypen char¶
charist Ganzzahl-Typ, idR. 1 ByteZeichen sind intern Ganzzahlen zugeordnet
- idR. ASCII-Code
- siehe z.B. http://www.asciitable.com/
- ASCII-Code eines Buchstabens erhält man durch einfache
Hochkommata
- Deklaration
char var = 'A';weistvarASCII-Code des BuchstabensAzu
- Deklaration
Platzhalter eines Zeichens für
printfundscanf%cals Zeichen%dals Ganzzahl
ACHTUNG:
'A'erzeugtchar,"A"erzeugtchar*
1 2 3 4 5 6 7 8 | #include <stdio.h>
int main() {
char var = 'A';
printf("sizeof(var) = %d\n", sizeof(var));
printf("%c %d\n",var,var);
}
|
sizeof(var) = 1 A 65
Gleitkommazahlen¶
Gleitkommadarstellung 1/3¶
SATZ: Zu existieren
- Vorzeichen
- Ziffern
- Exponent sodass gilt
Darstellung ist nicht eindeutig, da z.B.
- geometrische Reihe:
- z.B.
Bemerkungen zum Dezimalsystem¶
- Satz gilt für jede Basis
- Ziffern dann
- Dezimalsystem ist übliches System
- , , , ,
- Nichteindeutigkeit im Dezimalsystem:
Bemerkungen zum Binärsystem¶
Mit sind gekürzte Brüche genau dann als endliche Summe darstellbar (nicht als unendliche Reihe), wenn der Nenner Zweierpotenz ist:
- hat Nenner mit Zweierpotenz
- Eindeutigkeit der Primfaktorzerlegung
- formaler Beweis = freiwillige Übung
z.B. keine exakte Darstellung für für
Definition von Gleitkommazahlensystemen¶
Gleitkommazahlsystem
- endliche Teilmenge!
- Mantissenlänge
- Exponentialschranken
hat Darstellung mit
- Vorzeichen
- Ziffern mit oder
- normalisierte Gleitkommazahl ()
- denormalisierte Gleitkommazahl ()
- Exponent mit
Darstellung von ist eindeutig (Übung!)
- Ziffer muss nicht gespeichert werden
- implizites erstes Bit
Arithmetik für Gleitkommazahlen¶
- Ergebnis
Inf,-Infbei Überlauf (oder1./0.)- (
Inf), (-Inf)
- (
Ergebnis
NaN, falls nicht definiert (z.B.0./0.)- not a number (
NaN)
- not a number (
Arithmetik ist approximativ, nicht exakt
Genauigkeit nimmt ab wenn Zahlen größer werden, d.h., nur relative Fehler sind sinnvoll.
- Beispiel:
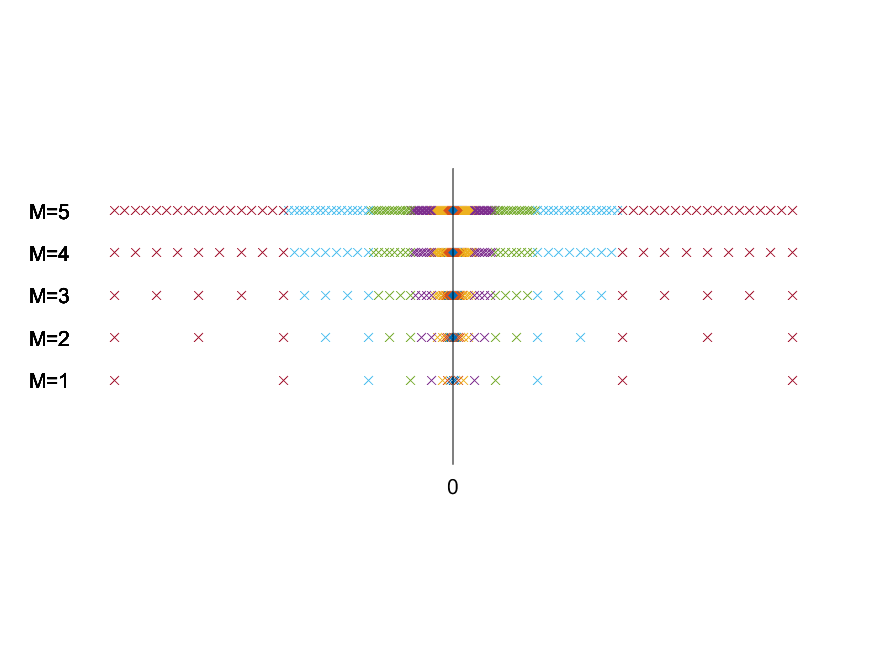
- Beispiel:
Schlechte Kondition¶
Eine Aufgabe ist numerisch schlecht gestellt bzw. schlecht konditioniert, falls kleine Änderungen der Daten auf große Änderungen im Ergebnis führen
- z.B. hat Dreieck mit gegebenen Seitenlängen einen rechten Winkel?
- z.B. liegt gegebener Punkt auf Kreisrand?
Implementierung sinnlos, weil Ergebnis zufällig!
bessere Fragestellungen:
- Hat ein Dreieck mit gegebenen Seitenlängen einen Winkel ?
- Liegt ein Punkt in einem -Schlauch um den Kreisrand?
Rechenfehler¶
- Aufgrund von Rechenfehlern darf man Gleitkommazahlen nie auf Gleichheit überprüfen
- Statt prüfen, ob Fehler klein ist
- z.B. mit
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | #include <stdio.h>
#include <math.h>
int main() {
double x = (116./100.)*100.;
printf("x=%f\n",x);
printf("floor(x)=%f\n",floor(x));
if (x==116.) {
printf("There holds x==116\n");
}
else {
printf("x = %.15f\n",x);
}
}
|
x=116.000000 floor(x)=115.000000 x = 115.999999999999986
Variablentypen float, double¶
floatist idR. einfache Genauigkeit nach IEEE-754-Standard- 4 Byte = 32 Bit
- 32b = 8b Exp. + 23b Mantisse + 1b Vorz.
- sog. single precision
- ca. 7 signifikante Dezimalstellen
- 4 Byte = 32 Bit
doubleist idR. doppelte Genauigkeit nach IEEE-754-Standard- 8 Byte = 64 Bit
- 64b = 11b Exp. + 52b Mantisse + 1b Vorz.
- sog. double precision
- ca. 16 signifikante Dezimalstellen
- 8 Byte = 64 Bit
Platzhalter in
printf:%a.bfgibtaStellen (inklusive '.') und davonbNachkommastellen aus%egibt Zahlen in Exponentialdarstellung aus
1 2 3 4 5 6 7 | #include <stdio.h>
int main() {
double x = 2./3.;
float y = 2./3.;
printf("%17.6f, %e\n", x, x);
printf("%16.15f, %.15e\n",y, y);
}
|
0.666667, 6.666667e-01 0.666666686534882, 6.666666865348816e-01