Was ist C++¶
- Weiterentwicklung von C
- Entwicklung ab 1979 bei AT&T
- Entwickler: Bjarne Stroustrup
- C++ ist abwärtskompatibel zu C
- C Programme funktionieren immer auch in C++
- aber: stärkere Zugriffskontrolle bei "Strukturen"
- Datenkapselung
- Compiler:
- frei verfügbar in Unix/Mac:
g++, gpp - Microsoft Visual C++ Compiler
- Borland C++ Compiler
- frei verfügbar in Unix/Mac:
Objektorientierte Programmiersprache¶
- C++ ist objektorientiertes C
- Objekt = Zusammenfassung von Daten + Funktionen.
- Funktionalität hängt von Daten ab
- vgl. Multiplikation für Skalar, Vektor, Matrix
- Befehlsreferenzen
Wie erstellt man ein C++ Programm?¶
Öffne eine (ggf. neue) Datei
name.cpp- Endung
.cppist Kennung für C++ Programm
- Endung
Schreibe Source-Code (= C++ Programm)
Source-Code abspeichern
Compilieren z.B. mit
g++ name.cppFalls Code fehlerfrei, erhält man Executable
a.out- unter Windows:
a.exe
- unter Windows:
Diese wird durch
a.outbzw../a.outgestartetCompilieren mit
g++ name.cpp -o outputerzeugt Executableoutputstatta.out
Hello World!¶
C++ Bibliothek für Ein- und Ausgabe ist
iostreammainhat zwingend Rückgabewertintint main()int main(int argc, char* argv[])- insbesondere
return 0;am Programmende
- insbesondere
Scope-Operator
::gibt Name Space an- alle Funktionen der Standardbibliotheken haben
std - Durch Konzept
lastname::firstnamekann man
- alle Funktionen der Standardbibliotheken haben
Funktionsnamen
firstnamemehrfach verwenden!- bei verschiedenen
lastname
- bei verschiedenen
std::coutist die Standard-Ausgabe (= Shell)- Operator
<<übergibt rechtes Argument - kann mehrere
<<mit einemstd::coutverwenden
- Operator
std::endlerzeugt neue Zeile (end of line)- ersetzt
\naus C
- ersetzt
1 2 3 4 5 6 | #include <iostream>
int main() {
std::cout << "Hello World!" << std::endl;
return 0;
}
|
Hello World!
Verwendung von using¶
Zeile 2:
using std::cout;coutgehört zum Name Spacestd- darf im Folgenden abkürzen
coutstattstd::cout
Zeile 3:
using std::endl;analogAlternativ auch
using namespace std(Achtung, führt leicht zu Fehlern bei späterer Verwendung von anderen Bibliotheken)
1 2 3 4 5 6 7 | #include <iostream>
using std::cout;
using std::endl;
int main () {
cout << "Hello World!" << endl;
return 0;
}
|
Shell-Input für main¶
<<arbeitet mit verschiedenen Typenkann mehrfache Ausgabe machen
<<Shell übergibt Input als C-Strings an Programm
- Parameter jeweils durch Leerzeichen getrennt
argc= Anzahl der Parameterargv= Vektor der Input-Stringsargv[0]= Programmname- d.h.
argc$-1$ echte Input-Parameter
1 2 3 4 5 6 7 8 9 10 11 12 | #include <iostream>
using std::cout;
using std::endl;
int main(int argc, char* argv[]) {
cout << "This is " << argv[0] << endl;
cout << "got " << argc-1 << " inputs:" << endl;
for (int j=1; j<argc; ++j) {
cout << j << ": " << argv[j] << endl;
}
return 0;
}
|
Eingabe / Ausgabe¶
std::cinist die Standard-Eingabe (= Tastatur)- Operator
>>schreibt Input in Variable rechts
- Operator
cin/coutgleichwertig mitprintf/scanfin C- aber leichter zu bedienen
- keine Platzhalter + Pointer
- Formatierung, siehe http://www.cplusplus.com
- $\longrightarrow$ ostream::operator<<
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <iostream>
int main(){
int x = 0;
double y = 0;
double z = 0;
std::cout << "Please enter an integer value: ";
std::cin >> x;
std::cout << "Please enter two double values: ";
std::cin >> y >> z;
std::cout << x << " * " << y << " / " << z;
std::cout << " = " << x*y/z << std::endl;
return 0;
}
|
Please enter an integer value: 4 Please enter two double values: 3.2 2.3 4 * 3.2 / 2.3 = 5.56522
Was ist neu in C++?¶
Datentyp bool¶
C kennt keinen Datentyp für Wahrheitswerte
- logischer Vergleich liefert $1$ für wahr, $0$ für falsch
- jede Zahl ungleich $0$ wird als wahr interpretiert
C++ hat Datentyp
boolfür Wahrheitswerte- Wert
truefür wahr,falsefür falsch - jede Zahl ungleich $0$ wird als wahr interpretiert
- Wert
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <iostream>
int main(){
double var = 0.3;
bool tmp = var;
if (1) {
std::cout << "1 is true\n";
}
if (var) {
std::cout << var << " is true\n";
}
if (tmp == true) {
std::cout << "equality is true\n";
}
if (0) {
std::cout << "0 is true\n";
}
return 0;
}
|
1 is true 0.3 is true equality is true
Funktionen in C++¶
- Default Parameter
1 2 3 | void f(int x, int y, int z = 0);
void g(int x, int y = 0, int z = 0);
void h(int x = 0, int y = 0, int z = 0);
|
kann Default-Werte für Input von Funktionen festlegen
- in der Signatur durch
=value - der Input-Parameter ist dann optional
- bekommt Default-Wert, falls nicht übergegeben
- in der Signatur durch
Beispiel: Zeile 1 erlaubt Aufrufe
f(x,y,z)f(x,y)undzbekommt implizit den Wertz = 0
1 2 3 | void f(int x = 0, int y = 0, int z); // syntax error
void g(int x, int y = 0, int z); // syntax error
void h(int x = 0, int y, int z = 0); // syntax error
|
- darf nur für hintere Parameter verwendet werden
- d.h. nach optionalem Parameter darf kein obligatorischer Parameter mehr folgen
- damit für den Compiler die Zuordnung der Übergabe-Parameter eindeutig ist anhand der Anzahl!
Weiteres zu Default Parametern¶
Default-Parameter darf nur einmal gegeben werden
d.h. Default-Parameter nur in Zeile 1 definieren!
Konvention: Default-Parameter nur im Header-File festlegen
brauche bei Forward Decl. keine Variablennamen
void f(int, int = 0);in Zeile 1 ist OK
1 2 3 4 | void f(int x, int y = 0);
void f(int x, int y = 0) { //Fehler
cout << "x=" << x << ", y=" << y << "\n";
}
|
Überladen von Funktionen¶
Mehrere Funktionen gleichen Namens möglich
- unterscheiden sich durch ihre Signaturen
Input muss Variante eindeutig festlegen
bei Aufruf wird die richtige Variante ausgewählt
- Compiler erkennt dies über Anzahl und Typen der Übergabe-Parameter
- Achtung mit implizitem Type Cast
Diesen Vorgang nennt man Überladen
Reihenfolge bei der Deklaration ist unwichtig
- d.h. kann Zeilen 1--3 beliebig permutieren
Rückgabewerte können unterschiedlich sein
- Also: unterschiedliche Output-Parameter
und gleiche Input-Parameter geht nicht
- Zeile 1 + 2 + 3: OK
- Zeile 4: gleicher Input wie Zeile 1
- Zeile 5: da optionaler Input und damit gleicher Input wie Zeile 1
- Also: unterschiedliche Output-Parameter
und gleiche Input-Parameter geht nicht
1 2 3 4 5 | void f(char*);
double f(char*, double);
int f(char*, char*, int = 1);
int f(char*); // syntax error
double f(char*, int = 0); // syntax error
|
Überladen vs. Default Parameter¶
- Mit Überladen und Default Parameter kann das gleiche Ziel erreicht werden.
1 2 3 4 5 6 7 8 | #include <iostream>
void drive_default(int km=10,int h=0){
std::cout << km << " km travelled";
if (h > 0) {
std::cout << " in " << h << " hour(s)";
}
std::cout << std::endl;
}
|
1 2 3 | void drive_overload(){
std::cout << "10 km travelled"<< std::endl;
}
|
1 2 3 | void drive_overload(int km){
std::cout << km << " km travelled"<< std::endl;
}
|
1 2 3 | void drive_overload(int km, int h){
std::cout << km << " km travelled in " << h << " hour(s)"<< std::endl;
}
|
- Die Funktionen
drive_default()unddrive_overload()liefern den gleichen Output.
1 2 3 4 5 6 7 8 9 | int main(){
drive_default();
drive_default(35);
drive_default(35,1);
drive_overload();
drive_overload(35);
drive_overload(35,1);
return 0;
}
|
10 km travelled 35 km travelled 35 km travelled in 1 hour(s) 10 km travelled 35 km travelled 35 km travelled in 1 hour(s)
Klassen & Objekte¶
Klassen sind (benutzerdefinierte) Datentypen
- erweitern
structaus C - bestehen aus Daten und Methoden
- Methoden = Fktn. auf den Daten der Klasse
- erweitern
Deklaration etc. wie bei Struktur-Datentypen
- Zugriff auf Members über Punktoperator
- sofern dieser Zugriff erlaubt ist!
- Zugriffskontrolle = Datenkapselung
formale Syntax:
class ClassName{ ... };Objekte = Instanzen einer Klasse
- entspricht Variablen dieses neuen Datentyps
- wobei Methoden nur 1x im Speicher liegen
später: Kann Methoden überladen
- d.h. Funktionalität einer Methode abhängig von Art des Inputs
später: Kann Operatoren überladen
- z.B. $x+y$ für Vektoren
später: Kann Klassen von Klassen ableiten
- sog. Vererbung
- z.B. $\mathbb C\supset\mathbb{R}\supset\mathbb{Q}\supset\mathbb{Z}\supset\mathbb{N}$
- dann: $\mathbb{R}$ erbt Methoden von $\mathbb C$ etc.
Zugriffskontrolle¶
Klassen (und Objekte) dienen der Abstraktion
- genaue Implementierung nicht wichtig
Benutzer soll so wenig wissen wie möglich
- sogenannte black-box Programmierung
- nur Ein- und Ausgabe müssen bekannt sein
Richtiger Zugriff muss sichergestellt werden
Schlüsselwörter
private,publicundprotectedprivate(Standard)- Zugriff nur von Methoden der gleichen Klasse
public- erlaubt Zugriff von überall
protected- teilweiser Zugriff von außen
- wird in der VO später behandelt ($\leadsto$ Vererbung)
Beispiel 1/2¶
Dreieck in $\mathbb{R}^2$ mit Eckpunkten
x,y,zBenutzer kann Daten
x,y,znicht lesen + schreibenget/setFunktionen inpublic-Bereich einbauen
Benutzer kann Methode
areaaufrufenBenutzer muss nicht wissen, wie Daten intern verwaltet werden
- kann interne Datenstruktur später leichter verändern, falls das nötig wird
- z.B. Dreieck kann auch durch einen Punkt und zwei Vektoren abgespeichert werden
Zeile 2:
private:kann weggelassen werden- alle Members/Methoden standardmäßig
private
- alle Members/Methoden standardmäßig
Zeile 7: ab
public:ist Zugriff frei
1 2 3 4 5 6 7 8 9 10 11 12 13 | #include <iostream>
class Triangle {
private:
double x[2]={0,0};
double y[2]={0,0};
double z[2]={0,0};
public:
void setX(double, double);
void setY(double, double);
void setZ(double, double);
double getArea();
};
|
- Deklarieren von Objekt
trivom TypTriangle - Nennt man auch Instanz einer Klasse
- Versucht man auf
privatemembers außerhalb der Klasse zuzugreifen, bekommt man einen Fehlermeldung - Zwingt zu set/get-Funktionen
1 2 | Triangle tri;
tri.x[0] = 1.0;
|
input_line_9:3:5: error: 'x' is a private member of '__cling_N52::Triangle'
tri.x[0] = 1.0;
^
input_line_8:3:10: note: declared private here
double x[2]={0,0};
^
Interpreter Error:
Methoden implementieren¶
Implementierung wie bei anderen Funktionen
- aber: direkter Zugriff auf Members der Klasse
Signatur:
type ClassName:: fctName(input)typeist Rückgabewert (double,voidetc.)input= Übergabeparameter wie in C
Wichtig (Zeile 19):
ClassName::vorfctName- d.h. Methode
fctNamegehört zuClassName
- d.h. Methode
Darf innerhalb von
ClassName::fctNameauf alle Members der Klasse direkt zugreifen (Zeile 16-17)- auch auf
private-Members
- auch auf
Zeile 1: Einbinden der
math.haus C
1 2 3 4 | void Triangle::setX(double x0, double x1) {
x[0] = x0;
x[1] = x1;
}
|
1 2 3 4 | void Triangle::setY(double y0, double y1) {
y[0] = y0;
y[1] = y1;
}
|
1 2 3 4 | void Triangle::setZ(double z0, double z1) {
z[0] = z0;
z[1] = z1;
}
|
1 2 3 4 5 | double Triangle::getArea() {
// use the 2x2 determinant formula to compute the area
return 0.5*fabs( (y[0]-x[0])*(z[1]-x[1])
- (z[0]-x[0])*(y[1]-x[1]) );
}
|
Methoden aufrufen 1/2¶
Aufruf wie Member-Zugriff bei C-Strukturen
- wäre in C über Funktionspointer analog möglich
getAreaagiert auf den Members vontri
- d.h.
x[0]in Implementierung entsprichttri.x[0]
1 2 3 4 5 6 7 | int main(){
Triangle tri;
tri.setX(0.0,0.0);
tri.setY(1.0,0.0);
tri.setZ(0.0,1.0);
std::cout << "area = " << tri.getArea() << std::endl;
}
|
area = 0.5
Methoden direkt implementieren¶
- kann Methoden auch in Klasse implementieren
- ist aber unübersichtlicher $\rightarrow$
besser nicht!- verhindert Bilden vernünftiger Bibliotheken, d.h., keine Trennung von Header-File und Source-Code möglich
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | class Triangle {
private:
double x[2];
double y[2];
double z[2];
public:
void setX(double x0, double x1) {
x[0] = x0;
x[1] = x1;
}
void setY(double y0, double y1) {
y[0] = y0;
y[1] = y1;
}
void setZ(double z0, double z1) {
z[0] = z0;
z[1] = z1;
}
double getArea() {
return 0.5*fabs( (y[0]-x[0])*(z[1]-x[1])
- (z[0]-x[0])*(y[1]-x[1]) );
}
};
|
Strukturen¶
- Strukturen = Klassen, wobei alle Members
public- d.h.
MyStruct=MyStructClass
- d.h.
- besser direkt
classverwenden
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | #include <iostream>
struct MyStruct {
double x[2];
double y[2];
double z[2];
};
class MyClass {
double x[2];
double y[2];
double z[2];
};
class MyStructClass {
public:
double x[2];
double y[2];
double z[2];
};
|
- Default-Qualifier in Klassen ist
private- vgl.
MyClassund Syntax-Fehler in Zeile 7
- vgl.
1 2 3 4 5 6 7 8 9 10 | int main(){
MyStruct var1;
MyClass var2;
MyStructClass var3;
var1.x[0] = 0;
var2.x[0] = 0; // syntax error: x is private in MyClass
var3.x[0] = 0;
return 0;
}
|
Klasse string¶
std::stringist eine vorimplementierte Klasse in C++- Wichtig:
string$\neq$char*, sondern mächtiger! - liefert eine Reihe nützlicher Methoden
+zum Zusammenfügenreplacezum Ersetzen von Teilstringslengthzum Auslesen der Länge u.v.m.c_strliefert Pointer aufchar*
- http://www.cplusplus.com/reference/string/string/
- Zeile 3: Einbinden der
stdio.haus C
1 2 3 4 5 6 7 8 9 10 11 12 | #include <iostream>
#include <string>
#include <cstdio>
int main(){
std::string str1 = "Hello";
std::string str2 = "World";
std::string str3 = str1 + " " + str2;
std::cout << str3 << "! ";
str3.replace(6,5, "Peter");
std::cout << str3 << "! ";
printf("%s?\n",str3.c_str());
}
|
Hello World! Hello Peter! Hello Peter?
Wozu Zugriffskontrolle?¶
Großteil der Entwicklungszeit geht in Fehlersuche von Laufzeitfehlern!
Möglichst viele Fehler bewusst abfangen!
- Fkt-Input auf Konsistenz prüfen, ggf. Abbruch
- garantieren, dass Funktions-Output zulässig!
- Zugriff kontrollieren mittels
getundset - reine Daten sollten immer
privatesein - Benutzer kann/darf Daten nicht verpfuschen!
- in C = soll nicht, in C++ = kann nicht!
Wie sinnvolle Werte sicherstellen?
- Zeile 10: Nenner eines Bruchs muss $\neq0$ sein
- mögliche Fehlerquellen direkt ausschließen
- Programm bestimmt, was Nutzer darf!
Try-Throw-Catch¶
- Was tun bei falschen/fehlerhaften Eingaben
- In C hatten wir
assert(...)zum kontrollierten Programmabbruch Ist in C++ auch verfügbar mit
#include <cassert>Besser: Try-Throw-Catch
- Nicht nur kontrollierter Abbruch, sonderen Fehlerbehandlung
1 2 3 4 5 6 7 | try{
//Code der ausgeführt werden soll
throw errorID; //wenn Fehler auftritt, Abbruch und Fehlerbehandlung
}
catch(type errorID) {
//Fehlerbehandlung
}
|
typedererrorIDkann jeder Datentyp sein- Es kann beliebig viele
catch()Blöcke geben, erster passender wird ausgeführt - Kein Typcasing by
errorID catch(...)fängt jeden Fehlertyp der kein eigenescatch()hatthrow xohne zugehörigescatch(type x)führt zu Programmabbruch ähnlich zuassert- Alternativ:
std::abort()beendet das Programm sofort (zum Beispiel Abbruch nach Fehlermeldung)
Beispiel: Klasse für Brüche mit Zugriffskontrolle¶
- Speicher Brüche als Zähler/Nenner (Numerator/Denominator)
- Stelle sicher, dass Nenner immer positiv ist $\rightarrow$ Zugriffsfunktionen
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <iostream>
#include <cassert>
class Fraction {
private:
int numerator = 0;
int denominator = 1;
public:
int getNumerator();
int getDenominator();
void setNumerator(int n);
void setDenominator(int n);
void print();
};
|
- Ausgabe des Bruchs mit
print()im Format3/4
1 2 3 | void Fraction::print() {
std::cout << numerator << "/" << denominator << std::endl;
}
|
- Lese- und Schreibfunktionen
1 2 3 | int Fraction::getNumerator() {
return numerator;
}
|
1 2 3 | void Fraction::setNumerator(int n) {
numerator = n;
}
|
1 2 3 | int Fraction::getDenominator() {
return denominator;
}
|
- Bei
setDenominator(int n)wollen wir das Vorzeichen immer im Zähler speichern und den Fehlern==0(Nenner ist Null) abfangen.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | void Fraction::setDenominator(int n) {
try{
// ensure that denominator is not 0
if (n==0) {
throw n;
}
// if n<0, store positive denominator and flip the sign of the numerator
if (n > 0) {
denominator = n;
} else {
denominator = -n;
numerator = -numerator;
}
}
catch(int n){
std::cout << "Denominator must not be zero!" << std::endl;
}
}
|
Die errorID ist in diesem Fall n. Mann könnte damit verschiedene Fehlertypen unterscheiden. Zum Beispiel den Fall $n<0$ und den Fall $n=0$. Im obigen Beispiel behandeln wir aber nur einen Fehlertyp.
1 2 3 4 5 6 7 8 | int main(){
Fraction x;
x.setNumerator(1);
x.setDenominator(3);
x.print();
x.setDenominator(0);
return 0;
}
|
1/3 Denominator must not be zero!
Konstruktor & Destruktor 1/2¶
- Konstruktor = automatisch bei Deklaration
- kann Initialisierung übernehmen
- kann verschiedene Aufrufe haben, z.B.
- Anlegen eines Vektors der Länge Null
- Anlegen eines Vektors $x\in\mathbb{R}^N$
und Initialisieren mit Null - Anlegen eines Vektors $x\in\mathbb{R}^N$ und Initialisieren mit gegebenem Wert
- formal:
ClassName( input)- kein Output, eventuell Input
- verschiedene Konstruktoren haben verschiedenen Input
- Standardkonstruktor:
ClassName()
Konstruktor & Destruktor 2/2¶
- Konstruktor kann überladen werden, z.B.
- kein Input $\rightarrow$Vektor der Länge Null
- ein Input
dim$\rightarrow$ Null-Vektor der Längedim - Input
dim,val$\rightarrow$ Vektor der Längedimmit Einträgenval
- Destruktor = automatisch bei Lifetime-Ende
- Freigabe von dynamischem Speicher
- es gibt nur Standarddestruktor:
~ClassName()- kein Input, kein Output
- kann insbesondere nicht überladen werden
Konstruktor: Ein Beispiel¶
- Konstruktor hat keine Rückgabe (Zeile 11 + 14)
ClassName( input)- Standardkonstruktor ohne Input (Zeile 11)
- Konstruktor kann (wie jede Methode) überladen werden (siehe Überladen von Funktionen)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <iostream>
#include <string>
using std::cout;
using std::string;
class Student {
private:
string lastname;
int student_id;
public:
Student() {
cout << "student registered\n";
}
Student(string name, int id) {
lastname = name;
student_id = id;
cout << "student registered (" << lastname;
cout << ", " << student_id << ")\n";
}
};
|
1 2 3 4 5 | int main(){
Student demo;
Student var("Feischl", 123456);
return 0;
}
|
student registered student registered (Feischl, 123456)
Namenskonflikt & Pointer "this"¶
thisgibt Pointer auf das aktuelle Objektthis->gibt Zugriff auf Member des aktuellen Objekts
Namenskonflikt in Konstruktor (Zeile 14)
- Input-Variablen heißen wie Members der Klasse
- d.h. Members verlieren Scope (Zeile 14-19)
- Zeile 14--16: Lösen des Konflikts mittels
this->
- Input-Variablen heißen wie Members der Klasse
- Warum? Ziel von schönem Code ist sprechende Variablennamen zu wählen. Daher will man
lastnameundstudent_idals Input-Variablen verwenden
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <iostream>
#include <string>
using std::cout;
using std::string;
class Student {
private:
string lastname;
int student_id;
public:
Student() {
cout << "student registered\n";
}
Student(string lastname, int student_id) {
this->lastname = lastname;
this->student_id = student_id;
cout << "student registered (" << lastname;
cout << ", " << student_id << ")\n";
}
};
|
1 2 3 4 5 | int main(){
Student demo;
Student var("Feischl",12345678);
return 0;
}
|
student registered student registered (Feischl, 12345678)
Destruktor: Ein Beispiel¶
- Zeile 20-23: Destruktor (ohne Input + Output)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | #include <iostream>
#include <string>
using std::cout;
using std::string;
class Student {
private:
string lastname;
int student_id;
public:
Student() {
cout << "student registered\n";
}
Student(string lastname, int student_id) {
this->lastname = lastname;
this->student_id = student_id;
cout << "student registered (" << lastname;
cout << ", " << student_id << ")\n";
}
~Student() {
cout << "student deleted (" << lastname << ", ";
cout << student_id << ")\n";
}
};
|
1 2 3 4 | int main(){
Student var("Feischl",12345678);
return 0;
}
|
student registered (Feischl, 12345678)
student deleted (Feischl, 12345678)
Methoden: Kurzschreibweise¶
- Zeile 11, 14-15: Kurzschreibweise für Zuweisung
- ruft entsprechende Konstruktoren auf
- eher schlecht lesbar
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | #include <iostream>
#include <string>
using std::cout;
using std::string;
class Student {
private:
string lastname;
int student_id;
public:
Student() : lastname("nobody"), student_id(0) {
cout << "student registered\n";
}
Student(string name, int id) :
lastname(name), student_id(id) {
cout << "student registered (" << lastname;
cout << ", " << student_id << ")\n";
}
~Student() {
cout << "student deleted (" << lastname << ", ";
cout << student_id << ")\n";
}
};
|
1 2 3 4 | int main(){
Student test;
return 0;
}
|
student registered
student deleted (nobody, 0)
Noch ein Beispiel¶
- Das Beispiel zeigt zu welchem Zeitpunkt die Konstruktoren und Destruktoren aufgerufen werden
- Grundsätzlich gilt: Objekten werden in umgekehrter Reihenfolge gelöscht.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | #include <iostream>
#include <string>
using std::cout;
using std::string;
class Test {
private:
string name;
public:
void print() {
cout << "name " << name << "\n";
}
Test() : name("Default") { print(); }
Test(string n) : name(n) { print(); }
~Test() {
cout << "delete " << name << "\n";
}
};
|
1 2 3 4 5 6 7 8 9 | int main(){
Test t1("Object1");
{
Test t2;
Test t3("Object3");
}
cout << "end of block" << "\n";
return 0;
}
|
name Object1 name Default name Object3 delete Object3 delete Default end of block delete Object1
Schachtelung von Klassen¶
- Klassen können geschachtelt werden
- Standardkonstruktor/-destruktor automatisch aufgerufen
- Konstruktoren der Member zuerst
- Destruktoren der Member zuletzt
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | #include <iostream>
using std::cout;
using std::endl;
class Class1 {
public:
Class1() { cout << "constr Class1" << endl; }
~Class1() { cout << "destr Class1" << endl; }
};
class Class2 {
private:
Class1 obj1;
public:
Class2() { cout << "constr Class2" << endl; }
~Class2() { cout << "destr Class2" << endl; }
};
|
1 2 3 4 | int main(){
Class2 obj2;
return 0;
}
|
constr Class1 constr Class2 destr Class2 destr Class1
Templates¶
- Ziel: Coder wiederverwendbar und flexibel gestalten
*Beispiel: Maximum berechnen / quadrieren
Gleicher Code für viele Probleme
- Lösung:
Templates
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | int max(int a, int b) {
if (a < b) {
return b;
}
else {
return a;
}
}
double max(double a, double b) {
if (a < b) {
return b;
}
else {
return a;
}
}
int square(int a) {
return a*a;
}
double square(double a) {
return a*a;
}
|
Funktionstemplate 1/2¶
template <typename Type> RetType fct( input)- analog zu normaler Funktionsdeklaration
Typeist dann variabler Input/Output-Datentyp- Pointer auf
Typemöglich
theoretisch mehrere variable Datentypen möglich
template <typename Type1, typename Type2>...
1 2 3 4 5 | #include <iostream>
template <typename Type>
Type square(const Type t) {
return t*t;
}
|
Funktion
squarekann aufgerufen werden, fallsvarObjekt vom TypType- Datentyp
Typehat Multiplikation*
bei Aufruf Datentyp in spitzen Klammern (Zeilen 2 und 4) oder implizit (Zeile 3)
- Compiler warnt vor implizitem Typecast in Zeile 4 (
doubleaufint)
- Compiler warnt vor implizitem Typecast in Zeile 4 (
1 2 3 4 5 | int main() {
std::cout << square<double>(1.5) << std::endl;
std::cout << square(1.5) << std::endl;
std::cout << square<int>(1.5) << std::endl;
}
|
input_line_9:4:28: warning: implicit conversion from 'double' to 'int' changes value from 1.5 to 1 [-Wliteral-conversion]
std::cout << square<int>(1.5) << std::endl;
~~~~~~ ^~~
2.25 2.25 1
- Was passiert eigentlich bei folgendem Code?
1 2 3 4 | int x = 2;
double y = 4.7;
std::cout << square(x) << std::endl;
std::cout << square(y) << std::endl;
|
4 22.09
- Compiler erkennt dass Funktion
squareeinmal für Typintund einmal für Typdoublebenötigt wird- Compiler erzeugt ("programmiert") und kompiliert anhand von dieser Information, zwei(!)
Funktionen mit der Signatur
double square(const double)int square(const int)
- d.h.
squareautomatisch durch Template generiert- also nur für die Typen, die wirklich benötigt
- Compiler erzeugt ("programmiert") und kompiliert anhand von dieser Information, zwei(!)
Funktionen mit der Signatur
Klassen-Template¶
- kann auch Templates für Klassen machen
- Syntax wie für Funktionen:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <iostream>
template <typename Type>
class ClassName {
private:
Type memberVar;
public:
void set(Type memberVar){
this->memberVar=memberVar;
}
Type get(){
return memberVar;
}
};
|
1 2 3 4 5 6 | int main(){
ClassName<double> var;
var.set(3.4);
std::cout << var.get() <<std::endl;
return 0;
}
|
3.4
C++ Standardcontainer¶
- C++ hat viele vordefinierte Klassen-Templates
list(verkettete Listen)queue(first-in-first-out)stack(last-in-first-out)deque(double ended queue)setmultisetmapmultimapvector
- Weitere C++ Bibliotheken
- Boost Library: Große Sammlung an Bib.
- http://www.boost.org
Das Vector Template¶
vectorist C++ Standardcontainer (und ein Klassen-Template)- kann beliebige Datentypen verwenden
- dienen zum Verwalten von Datenmengen (Array mit viel mehr Funktionalität)
Beispiel: Vector mit Einträgen aus eigener Klasse
Entry
1 2 3 4 5 6 7 8 9 10 11 | #include <iostream>
#include <string>
#include <vector>
using std::vector;
using std::string;
class Entry {
public:
string firstname;
string lastname;
};
|
Zeile 2 unten: Anlegen eines Vektors der Länge 2 mit Einträgen vom Typ
EntryAnlegen
vector<type> name(size);- Achtung, nicht verwechseln:
- 1000 Einträge:
vector<Entry> buch(1000); - 1000 Vektoren:
vector<Entry> buch[1000];
- 1000 Einträge:
- Zugriff auf $j$-tes Element wie bei Arrays
telephoneBook[j](Zeile 3-6, 8 unten)
1 2 3 4 5 6 7 8 9 10 11 | int main(){
vector<Entry> telephoneBook(2);
telephoneBook[0].firstname = "Peter";
telephoneBook[0].lastname = "Pan";
telephoneBook[1].firstname = "Wolverine";
telephoneBook[1].lastname = "";
for(int i=0;i<2;++i){
std::cout << telephoneBook[i].firstname << " " << telephoneBook[i].lastname <<std::endl;
}
return 0;
}
|
Peter Pan Wolverine
Weitere Eigenschaften von vector 1/2¶
- Funktionalität von dynamischem Speicher, aber mit automatischer Speicherverwaltung
- kein
free,malloc, ...
- kein
- automatische Initialisierung (Zeile 3-6)
sizeliefert die Länge des Vektors- Intern wird immer etwas mehr Speicher allokiert, als für die Länge des Vektors notwendig ist. Mittels
capacitykann man die Größe des allokierten Speichers abfragen.
- Intern wird immer etwas mehr Speicher allokiert, als für die Länge des Vektors notwendig ist. Mittels
- Änderung der Länge mit
resize()(Zeile 10). Achtung: fallsresizeden Vektor verlängert muss Speicher neu allokiert werden (sollte man nicht zu oft machen, da teuer) - Vertauschen von zwei Vektoren mittels
swap()(Zeile 19, keine Hilfsvariable nötig) =ist deep-copy
1 2 3 | #include <iostream>
#include <vector>
using std::vector;
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | int main(){
vector<double> test(10,3);
vector<double> var;
vector<int> a(5,1);
vector<int> b(10,2);
std::cout << "test[3] = " << test[3] <<std::endl;
test[4]=10;
std::cout<< "length of test: " << test.size()<<std::endl;
test.resize(20,4);
std::cout << "test[13] = " << test[13] <<std::endl;
std::cout<< "length of test: " << test.size()<<std::endl;
var = test;
var[13]=0;
std::cout << "var[13] = " << var[13] <<std::endl;
std::cout << "test[13] = " << test[13] <<std::endl;
a.swap(b);
for(int i=0;i<a.size();++i){
std::cout << a[i] << " ";
}
std::cout << std::endl;
for(int i=0;i<b.size();++i){
std::cout << b[i] << " ";
}
std::cout << std::endl;
return 0;
}
|
test[3] = 3 length of test: 10 test[13] = 4 length of test: 20 var[13] = 0 test[13] = 4 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1
Weitere Eigenschaften von vector 2/2¶
clearlöscht alle Einträge und setzt die Länge des Vektors auf Nullpush_backhängt einen neuen Eintrag am Ende des Vektors an und verlängert diesen um Eins. (Achtung: wenn man viele Elemente anhängen will und die Performance wichtig ist, besser mitresizeum häufiges Neuallokieren zu vermeiden)pop_backlöscht den letzten Eintrag des Vektors und verkürzt diesen um Eins.
1 2 3 | #include <iostream>
#include <vector>
using std::vector;
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | int main(){
vector<double> test(1,1);
test.push_back(2);
test.push_back(1);
test.push_back(3);
for(int i=0;i<test.size();++i){
std::cout << test[i] << " ";
}
std::cout << std::endl;
test.pop_back();
for(int i=0;i<test.size();++i){
std::cout << test[i] << " ";
}
std::cout << std::endl;
test.clear();
std::cout << "Length of test: " << test.size() << std::endl;
return 0;
}
|
1 2 1 3 1 2 1 Length of test: 0
Vektoren mittels vector¶
- Obwohl der Vectorcontainer (Vektor-Template) schon sehr viel kann, macht es manchmal Sinn eine eigene Klasse zu implementieren um zusätzliche Funktionalität zu erhalten.
vectorTemplate hat Methodesize(Zeile 25)- wird genutzt für Methode
size()für KlasseVector - Zusätzlich noch
norm()und Lese-/Schreibfunktionen mit Fehlerbehandlung
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | #include <iostream>
#include <vector>
#include <cmath>
using std::vector;
class Vector {
private:
vector<double> coeff;
public:
Vector(int dim=0, double init=0);
double get(int k);
void set(int k, double val);
int size();
double norm();
};
|
- Konstruktor nutzt Kurzschreibweise und Konstruktor vom Vektor-Template
1 | Vector::Vector(int dim, double init) : coeff(dim,init) {}
|
1 2 3 | int Vector::size(){
return coeff.size();
}
|
1 2 3 4 5 6 7 | double Vector::norm(){
double sum = 0;
for (int j=0; j<size(); ++j) {
sum = sum + coeff[j]*coeff[j];
}
return sqrt(sum);
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | double Vector::get(int k) {
double tmp;
try{
if(k<0 || k>coeff.size()){
throw k;
}else{
return coeff[k];
}
}
catch(int n){
std::cout << "Warning: accessing out of bounds element (" << n <<"), returning zero" << std::endl;
return 0;
}
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 | void Vector::set(int k, double val) {
double tmp;
try{
if(k<0 || k>coeff.size()){
throw k;
}else{
coeff[k] = val;
}
}
catch(int n){
std::cout << "Warning: accessing out of bounds element (" << n <<"), no assignement" << std::endl;
}
}
|
1 2 3 4 5 6 7 | int main(){
Vector vec(5,1);
vec.set(3,3);
std::cout << vec.get(3);
std::cout << vec.norm();
return 0;
}
|
33.60555
Matrizen mittels vector¶
- Wieder zwei Möglichkeiten
- Spaltenweise Speicherung (sehr ähnlich zu Klasse
Vector) - Matrix Speicherung mit geschachtelten Templates
- Spaltenweise Speicherung (sehr ähnlich zu Klasse
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | #include <iostream>
#include <vector>
#include <cmath>
using std::vector;
class Matrix {
private:
vector<vector<double> > coeff;
public:
Matrix(int n=0, int m=0, double init=0);
double get(int i, int j);
void set(int i, int j, double val);
int getN();
int getM();
double frobeniusNorm();
};
|
- Beachte Abstand bei
> >in Zeile 11 oben,>>ist Stream Operator - kein dynamischer Speicher notwendig, wird durch das Vector-Template alles intern erledigt!
1 | Matrix::Matrix(int n, int m, double init) : coeff(n,vector<double>(m, init)) {}
|
1 2 3 | int Matrix::getN(){
return coeff.size();
}
|
1 2 3 4 5 6 | int Matrix::getM(){
if(getN()==0){
return 0;
}
return coeff[0].size();
}
|
- Die Frobenius-Norm ist eine der einfachsten Matrixnormen $$ M\in\mathbb{R}^{n\times m},\quad \|M\|_F := \sqrt{\sum_{i=0}^{n-1}\sum_{j=0}^{m-1} M_{ij}^2} $$
1 2 3 4 5 6 7 8 9 | double Matrix::frobeniusNorm(){
double sum = 0;
for (int i=0; i<getN(); ++i) {
for(int j=0;j<getM(); ++j){
sum = sum + coeff[i][j]*coeff[i][j];
}
}
return sqrt(sum);
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | double Matrix::get(int i,int j) {
double tmp;
try{
if(i<0 || i>getN() || j<0 || j>getM()){
throw i;
}else{
return coeff[i][j];
}
}
catch(int n){
std::cout << "Warning: accessing out of bounds element, returning zero" << std::endl;
return 0;
}
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 | void Matrix::set(int i, int j, double val) {
double tmp;
try{
if(i<0 || i>getN() || j<0 || j>getM()){
throw i;
}else{
coeff[i][j] = val;
}
}
catch(int n){
std::cout << "Warning: accessing out of bounds element, no assignement" << std::endl;
}
}
|
- Matrix-Vektor Produkt als Funktion von
MatrixundVector - Formel $M\in\mathbb{R}^{n\times m}, x\in\mathbb{R}^m$ $$ y_i = \sum_{j=0}^{m-1} M_{ij}x_j,\quad\text{ for all }i=1,\ldots,m $$
1 2 3 4 5 6 7 8 9 10 11 | Vector matrixVectorProd(Matrix M, Vector x){
Vector result(M.getN(),0);
for(int i=0; i<M.getN(); ++i){
double tmp=0;
for(int j=0; j<M.getM(); ++j){
tmp += M.get(i,j)*x.get(j);
}
result.set(i,tmp);
}
return result;
}
|
- Beim Funktionsaufruf in Zeile 4 unten erfolgt Call-by-Value und daher werden 'M' und 'x' auf lokale Variablen kopiert (deep copy). Das kann sehr teuer sein.
- Daher: verwende besser Call-by-Value mittels Referenzen (nächstes Kapitel)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | int main(){
Matrix M(4,5,1);
Vector x(5,1);
Vector y = matrixVectorProd(M,x);
M.set(3,3,10);
std::cout << "M(3,3) = " << M.get(3,3) << ", M(3,4) = " << M.get(3,4) <<std::endl;
std::cout << "||M||_F = "<< M.frobeniusNorm() << std::endl;
std::cout << "M*x = (";
for(int i=0;i<y.size();++i){
std::cout << y.get(i) << " ";
}
std::cout << ")" << std::endl;
return 0;
}
|
M(3,3) = 10, M(3,4) = 1 ||M||_F = 10.9087 M*x = (5 5 5 5 )
Referenzen in C++ (=Pointer light)¶
Referenzen sind Aliasnamen für Objekte/Variablen
- d.h. kein neuer Speicher
- nur zusätzlicher Name für existierendes Objekt
type& ref = var;- erzeugt eine Referenz
refzuvar varmuss vom Datentyptypesein- Referenz muss bei Definition initialisiert werden!
- erzeugt eine Referenz
nicht verwechselbar mit Address-Of-Operator
type&ist Referenz&var liefert Speicheradresse vonvar
1 2 3 4 5 6 7 8 9 10 11 12 13 | #include <iostream>
int main() {
int var = 5;
int& ref = var;
std::cout << "var = " << var << std::endl;
std::cout << "ref = " << ref << std::endl;
ref = 7;
std::cout << "var = " << var << std::endl;
std::cout << "ref = " << ref << std::endl;
return 0;
}
|
var = 5 ref = 5 var = 7 ref = 7
- muss: Deklaration + Initialisierung (Zeile 4)
- sind nur Alias-Name für denselben Speicher
- d.h.
refundvarsind symbolische Namen für dieselbe Adresse
1 2 3 4 5 6 7 8 9 10 11 12 | #include <iostream>
int main() {
int var = 5;
int& ref = var;
std::cout << "var = " << var << std::endl;
std::cout << "ref = " << ref << std::endl;
printf("address of var = %p\n",&var);
printf("address of var = %p\n",&ref);
return 0;
}
|
var = 5 ref = 5 address of var = 0x7ffd3f3b3588 address of var = 0x7ffd3f3b3588
Call-by-Reference mittels Pointer¶
bereits bekannt aus C:
- übergebe Adressen
&x,&ymit Call-by-Value - lokale Variablen
px,pyvom Typint* - Zugriff auf Speicherbereich von
xdurch Dereferenzieren*px - analog für
*py
- übergebe Adressen
Zeile 6-8: Vertauschen der Inhalte von
*pxund*py
1 2 3 4 5 6 | #include <iostream>
void swap(int* px, int* py) {
int tmp = *px;
*px = *py;
*py = tmp;
}
|
1 2 3 4 5 6 7 8 | int main() {
int x = 5;
int y = 10;
std::cout << "x = " << x << ", y = " << y << std::endl;
swap(&x, &y);
std::cout << "x = " << x << ", y = " << y << std::endl;
return 0;
}
|
x = 5, y = 10 x = 10, y = 5
Call-by-Reference mittels Referenzen¶
echtes Call-by-Reference in C++
- Funktion kriegt Input als Referenzen
- Syntax:
type fctName( ..., type& ref, ... )- Input
refwird als Referenz übergeben - Call-by-Value und Call-by-Reference für verschiedene Parameter möglich!
- Input
rxist lokaler Name (Zeile 5-9) für den
Speicherbereich vonx(Zeile 12-17)analog für
ryundyAchtung: Bei Aufruf einer Funktion sieht man nicht, ob Call-by-Value oder Call-by-Reference
1 2 3 4 5 6 | #include <iostream>
void swap(int& rx, int& ry) {
int tmp = rx;
rx = ry;
ry = tmp;
}
|
1 2 3 4 5 6 7 8 | int main() {
int x = 5;
int y = 10;
std::cout << "x = " << x << ", y = " << y << std::endl;
swap(x, y);
std::cout << "x = " << x << ", y = " << y << std::endl;
return 0;
}
|
x = 5, y = 10 x = 10, y = 5
Beispiel: Matrix-Vektor Produkt¶
Signatur
Vector matrixVectorProd(Matrix M, Vector x)realisiert Call-by-Value- d.h.
Mundxwerden beim Aufruf in lokale Variablen kopiert kann sehr teuer sein
Abhilfe: Call-by-Reference mit Referenzen
- einzige Änderung ist Signatur in Zeile 1
- d.h.
1 2 3 4 5 6 7 8 9 10 11 | Vector matrixVectorProd(Matrix& M, Vector& x){
Vector result(M.getN(),0);
for(int i=0; i<M.getN(); ++i){
double tmp=0;
for(int j=0; j<M.getM(); ++j){
tmp += M.get(i,j)*x.get(j);
}
result.set(i,tmp);
}
return result;
}
|
Referenzen vs. Pointer¶
Referenzen sind Aliasnamen für Variablen
- müssen bei Deklaration initialisiert werden
- kann Referenzen nicht nachträglich zuordnen!
keine vollständige Alternative zu Pointern, da ...
- keine Mehrfachzuweisung
- kein dynamischer Speicher möglich
- keine Arrays von Referenzen möglich
- Referenzen dürfen nicht
NULLsein
Achtung: Syntax verschleiert Programmablauf
- bei Funktionsaufruf nicht klar, ob Call by Value oder Call by Reference
- anfällig für Laufzeitfehler, wenn Funktion Daten ändert, aber Hauptprogramm das nicht weiß
- passiert bei Pointern nicht
Wann Call by Reference sinnvoll?
- falls Input-Daten umfangreich
- z.B. "große" Matrizen oder "lange" Vektoren
- denn Call by Value kopiert Daten
- dann Funktionsaufruf billiger
- falls Input-Daten umfangreich
Range based for-Schleife¶
- Schleife iteriert automatisch über gesamten Vektor (oder andere Container)
- Nützlich um, z.B., die selbe Funktion auf jedes Element des Vektors anzuwenden
- In anderen Programmiersprachen heißt diese Schleife auch oft
for-each
1 2 3 | #include <iostream>
#include <vector>
using std::vector;
|
1 2 3 4 5 6 7 | int main(){
vector<double> vec(10,3);
for(double x : vec){
std::cout << x <<" ";
}
std::cout << std::endl;
}
|
3 3 3 3 3 3 3 3 3 3
- Elemente verändern über Referenzen
1 2 3 4 5 6 7 8 9 10 | int main(){
vector<double> vec(10,3);
for(double& x : vec){
x = x*x+10;
}
for(double x : vec){
std::cout << x <<" ";
}
std::cout << std::endl;
}
|
19 19 19 19 19 19 19 19 19 19
Range based for-Schleife¶
- Funktioniert für alle Objekte, die Iteratoren implementiert haben. Dazu gehören
- Objekte vom Typ
std::vector - Statische Arrays
- Alle anderen Container-Klassen in C++
strings
- Objekte vom Typ
- Reihenfolge der
for-Schleife hängt von Objekt ab. Bei Arrays immer von vorne nach hinten - Funktioniert nicht für dynamische Arrays (mit
mallocodernew(später)) - Iteratoren sind Methoden, die das Abarbeiten von Elementen in einer Menge erlauben
- Man kann Iteratoren auch für benutzerdefinierte Klassen schreiben (nicht in EPROG)
1 2 3 | #include <iostream>
#include <string>
using std::string;
|
1 2 3 4 5 6 7 8 9 10 11 12 | int main(){
string name = "Michael Feischl";
double x[5] = {1,2,3,4,5};
for(char c : name){
std::cout << c << "_";
}
std::cout<<std::endl;
for(double y : x){
std::cout << y << "_";
}
return 0;
}
|
M_i_c_h_a_e_l_ _F_e_i_s_c_h_l_ 1_2_3_4_5_
Referenzen als Funktions-Output¶
Referenzen können Output von Funktionen sein
- nur sinnvoll bei Methoden (Objekten) (gleich!)
wie bei Pointern auf Lifetime achten!
- Referenz wird zurückgegeben (Zeile 5)
- aber Speicher wird freigegeben, da Blockende!
1 2 3 4 5 6 | #include <iostream>
int& fct() {
int x = 4711;
return x;
}
|
input_line_57:3:10: warning: reference to stack memory associated with local variable 'x' returned [-Wreturn-stack-address]
return x;
^
1 2 3 4 5 | int main() {
int& var = fct();
std::cout << "var = " << var << std::endl;
return 0;
}
|
var = 0
Referenzen als Methoden-Output¶
- Speicher ist Teil der Klasse und bleibt daher bestehen auch nach Ende der Methode
- Beispiel: eine einzige Funktion für set und get
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | #include <iostream>
#include <vector>
#include <cmath>
using std::vector;
using std::cout;
using std::ostream;
class Vector {
private:
vector<double> coeff;
public:
Vector(int dim=0, double init=0);
double& get(int k);
int size();
double norm();
};
|
1 | Vector::Vector(int dim, double init) : coeff(dim,init) {}
|
1 2 3 | int Vector::size(){
return coeff.size();
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 | double& Vector::get(int k) {
double tmp;
try{
if(k<0 || k>coeff.size()){
throw k;
}else{
return coeff[k];
}
} catch(int n){
std::cout << "Accessing out of bounds element, abort!" <<std::endl;
std::abort(); //terminate program
}
}
|
- Der Aufrug
x.get(3)in Zeile 4 unten liefert eine Referenz aufcoeff[3]zurück. Daher kanncoeff[3]verändert werden.
1 2 3 4 5 6 7 | int main(){
Vector x(10,1);
std::cout << x.get(3) << std::endl;
x.get(3)=5;
std::cout << x.get(3) << std::endl;
return 0;
}
|
1 5
Elementare Konstanten¶
möglich über
#define CONST wert- einfache Textersetzung
CONSTdurchwert - fehleranfällig & kryptische Fehlermeldung
- falls
wertSyntax-Fehler erzeugt
- falls
- Konvention: Konstantennamen groß schreiben
- einfache Textersetzung
besser als konstante Variable
- z.B.
const int var = wert; - z.B.
int const var = wert;- beide Varianten haben dieselbe Bedeutung!
- wird als Variable angelegt, aber Compiler verhindert Schreiben
- zwingend Initialisierung bei Deklaration
- z.B.
Achtung bei Pointern
const int* ptrist Pointer aufconst intint const* ptrist Pointer aufconst int- beide Varianten haben dieselbe Bedeutung!
- d.h.
*ptrist vom Typconst int - d.h.
*ptrkann nur lesen, nicht schreiben!
int* const ptrist konstanter Pointer aufint- d.h.
ptrkann nicht geändert werden - aber
*ptrkann lesen und schreiben!
- d.h.
Tipp: Um C/C++ Deklarationen zu verstehen einfach rückwärts lesen
const int* ptrbedeutet:ptrist Pointer (*) aufconst intint* const ptrbedeutet:ptristconstPointer (*) aufint
Einfache Beispiele zu const¶
varist nur lesbar- Syntax-Fehler beim Kompilieren:
1 2 3 4 5 | int main() {
const double var = 5;
var = 7;
return 0;
}
|
input_line_13:3:7: error: cannot assign to variable 'var' with const-qualified type 'const double' var = 7; ~~~ ^ input_line_13:2:16: note: variable 'var' declared const here const double var = 5; ~~~~~~~~~~~~~^~~~~~~
Interpreter Error:
varistconst double, aber*ptr istdouble
1 2 3 4 5 6 7 8 | int main() {
const double var = 5;
double tmp = 0;
double* const ptr = &var;
ptr = &tmp;
*ptr = 7;
return 0;
}
|
input_line_15:4:17: error: cannot initialize a variable of type 'double *const' with an rvalue of type 'const double *'
double* const ptr = &var;
^ ~~~~
Interpreter Error:
- zwei Syntax-Fehler beim Kompilieren:
- Zuweisung auf Pointer
ptr(Zeile 5) - Dereferenzieren und Schreiben (Zeile 6)
- Zuweisung auf Pointer
1 2 3 4 5 6 7 8 | int main() {
const double var = 5;
double tmp = 0;
const double* const ptr = &var;
ptr = &tmp;
*ptr = 7;
return 0;
}
|
input_line_17:5:7: error: cannot assign to variable 'ptr' with const-qualified type 'const double *const' ptr = &tmp; ~~~ ^ input_line_17:4:23: note: variable 'ptr' declared const here const double* const ptr = &var; ~~~~~~~~~~~~~~~~~~~~^~~~~~~~~~ input_line_17:6:8: error: read-only variable is not assignable *ptr = 7; ~~~~ ^
Interpreter Error:
Read-Only Referenzen¶
const type& cref- deklariert Referenz auf
const type- alternative Syntax:
type const& cref
- alternative Syntax:
- d.h.
crefist wie Variable vom Typconst type - Zugriff über Referenz nur lesend möglich
- deklariert Referenz auf
Zeile 13:
cref = 9;würde Syntaxfehler liefern
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #include <iostream>
int main() {
double var = 5;
double& ref = var;
const double& cref = var;
std::cout << "var = " << var << ", ";
std::cout << "ref = " << ref << ", ";
std::cout << "cref = " << cref << std::endl;
ref = 7;
std::cout << "var = " << var << ", ";
std::cout << "ref = " << ref << ", ";
std::cout << "cref = " << cref << std::endl;
// cref = 9;
return 0;
}
|
var = 5, ref = 5, cref = 5 var = 7, ref = 7, cref = 7
Read-Only Referenzen als Output¶
- Referenzen als Output ist oft effizient (da z.B. lange Vektoren nicht kopiert werden)
- Referenzen erlauben aber Zugriff auf private members (eigentlich nicht gewollt)
Abhilfe: Read-Only Referenzen
Beispiel: Matrix-Klasse hat Methode
getRow(int i)welche die i-te Zeile als Vektor zurückgibt. Man soll den Vektor aber nur lesen und nicht verändern können (Zum Beispiel um das Matrix-Vektor-Produkt zu berechnen).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #include <iostream>
#include <vector>
#include <cmath>
class Matrix {
private:
std::vector<std::vector<double> > coeff;
public:
Matrix(int n=0, int m=0, double init=0);
const std::vector<double>& getRow(int i);
std::vector<double>& getRowNonConst(int i);
double get(int i, int j);
};
|
1 | Matrix::Matrix(int n, int m, double init) : coeff(n,std::vector<double>(m, init)) {}
|
- Um den Unterschied zu veranschaulichen, implementieren wir zwei Version der Methode:
getRow()undgetRowNonConst()
1 2 3 | const std::vector<double>& Matrix::getRow(int i){
return coeff[i];
}
|
1 2 3 | std::vector<double>& Matrix::getRowNonConst(int i){
return coeff[i];
}
|
1 2 3 | double Matrix::get(int i,int j) {
return coeff[i][j];
}
|
- Definition in Zeile 4 unten erlaubt den Zugriff auf
privateVariablecoeffin Zeile 6- Diese Möglichkeit will man oft unterbinden
- Daher, Version mit Read-only Referenz in Zeile 3 führt zu Syntax Fehler in Zeile 6
1 2 3 4 5 6 7 8 | int main(){
Matrix M(4,4,0);
//const std::vector<double>& row = M.getRow(0);
std::vector<double>& row = M.getRowNonConst(0);
row[2]=5; //Ungewollter Zugriff auf private member coeff. Liefert Syntax Fehler bei Read-Only Reference
std::cout << M.get(0,2) << std::endl;
}
|
5
Type Casting¶
consttype ist stärker alstype- kein Type Casting von
consttype auftype
- kein Type Casting von
Type Casting von
typeaufconsttype ist aber OK!
1 2 3 4 5 | int main(){
Matrix M(4,4,0);
std::vector<double>& row = M.getRow(0); //Fehler, da const auf non-const gecasted werden soll
const std::vector<double>& row = M.getRowNonConst(0); //Okay, da non-const auf const gecasted wird
}
|
- Weiteres Beispiel
1 2 3 4 5 | #include <iostream>
double square(double& x) {
return x*x;
}
|
- Funktion mit nicht-const Parameter wird mit const-Variable aufgerufen
- Fehler, da Typecast von const auf non-const nicht erlaubt ist
- Mögliche Lösung: Signatur der Funktion of const ändern
1 2 3 4 5 6 | int main() {
const double var = 5;
std::cout << "var = " << var << ", ";
std::cout << "var*var = " << square(var) << std::endl;
return 0;
}
|
input_line_9:4:32: error: no matching function for call to 'square'
std::cout << "var*var = " << square(var) << std::endl;
^~~~~~
input_line_8:1:8: note: candidate function not viable: 1st argument ('const double') would lose const qualifier
double square(double& x) {
^
Interpreter Error:
Read-Only Referenzen als Input¶
- Nützlich, wenn man weiß, dass Input-Parameter nicht verändert werden
- Schneller Funktionsaufruf und man verhindert zusätzlich ungewollte Manipulation der Daten
Beispiel 1: Kopierkonstruktor¶
ClassName::ClassName(const ClassName& input)- erzeugt ein neues Objekt der Klasse
- als Kopie eines Objektes
input- also Input als Referenz auf konstantes Objekt
spezieller Konstruktor für den Aufruf
ClassName x = input;- oder äquivalent:
ClassName x(input);
wird auch bei Funktionen / Methoden verwendet
- für Call by Value für Input-Parameter
- für Rückgabe (wenn Wert und nicht Referenz)
wird automatisch erstellt (als Shallow Copy), falls nicht explizit programmiert
- Fehlen liefert in der Regel Laufzeitfehler, falls die Klasse dynamische Daten hat
Kopierkonstruktor kann auf private Members von
inputzugreifen- praktisch für
member = input.member
- praktisch für
1 2 3 4 5 6 7 8 9 10 11 | #include <iostream>
class Complex {
private:
double real;
double imag;
public:
Complex(double real, double imag);
Complex(const Complex& input); //Copy-constructor
};
|
1 2 3 4 | Complex::Complex(double real, double imag){
this->real = real;
this->imag = imag;
}
|
- Der Kopierkonstruktor kann auf
privatemembers der Klasse zugreifen (da selbst Teil der Klasse) - Hier wird nur zur Verdeutlichung eine Ausgabe implementiert
- Da die Klasse Complex keinen dynamischen Speicher hat, würde die automatische Implementierung ausreichen
1 2 3 4 5 | Complex::Complex(const Complex& input){
real = input.real;
imag = input.imag;
std::cout << "Copy-Constructor" << std::endl;
}
|
1 2 3 4 | Complex doNothing(Complex c){
std::cout << "inside function" << std::endl;
return c;
}
|
1 2 3 4 5 6 7 | int main(){
Complex a(1,2);
Complex b(0,0);
std::cout << "function call" << std::endl;
b = doNothing(a);
return 0;
}
|
function call Copy-Constructor inside function Copy-Constructor
Beispiel 2: Zuweisungsoperator¶
1 2 3 4 5 6 | ClassName& ClassName::operator=(const ClassName& input) {
if (this != &input) {
...
}
return *this;
}
|
ClassName& ClassName::operator=(const ClassName&)Falls
ClassName output, input;bereits deklariert:- Implementierung der Zuweisung
output = input; - Input als konstante Referenz (read-only)
- Rückgabe
return *this;für Zuweisungsketten- z.B.
a = b = c = d; =weist von rechts nach links zu!a = ...braucht Auswertung vonb = c = d;- erlaubt in C/C++, aber eher schlechter Stil!
- z.B.
- Implementierung der Zuweisung
Achtung: Zuweisungsoperator
- muss ggf. dynamischen Speicher von
outputfreigeben, da sonst toter Speicher entsteht - muss Selbstzuweisung
a = a;absichern - muss
return *this;zurückgeben
- muss ggf. dynamischen Speicher von
wird automatisch erstellt (als Shallow Copy), falls nicht explizit programmiert
- Fehlen liefert in der Regel Laufzeitfehler, falls die Klasse dynamische Daten hat
1 2 3 4 5 6 7 8 9 10 11 | #include <iostream>
class Complex {
private:
double real;
double imag;
public:
Complex(double real, double imag);
Complex(const Complex& input);
Complex& operator=(const Complex& input);
};
|
1 | Complex::Complex(double real, double imag): real(real), imag(imag){}
|
1 2 3 4 5 | Complex::Complex(const Complex& input){
real = input.real;
imag = input.imag;
std::cout << "Copy-Constructor" << std::endl;
}
|
1 2 3 4 5 6 7 8 | Complex& Complex::operator=(const Complex& input){
if (this != &input) {
real = input.real;
imag = input.imag;
std::cout << "assignement operator" << std::endl;
}
return *this;
}
|
1 2 3 4 | Complex doNothing(Complex c){
std::cout << "inside function" << std::endl;
return c;
}
|
1 2 3 4 5 6 7 8 9 10 11 | int main(){
Complex a(1,2);
Complex b(0,0);
std::cout << "assignement" << std::endl;
a=b;
std::cout << "self assignement" << std::endl;
a=a;
std::cout << "function call" << std::endl;
b = doNothing(a);
return 0;
}
|
assignement assignement operator self assignement function call Copy-Constructor inside function Copy-Constructor assignement operator
Beispiel 3: Effiziente Parameterübergabe im Skalarprodukt¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | #include <iostream>
#include <vector>
#include <cmath>
using std::vector;
class Vector {
private:
vector<double> coeff;
public:
Vector(int dim=0, double init=0);
double& get(int k);
int size();
double norm();
};
|
1 2 3 | double& Vector::get(int k){
return coeff[k];
}
|
1 2 3 | int Vector::size(){
return coeff.size();
}
|
Read-only Referenz als Input von Skalar-Produkt macht Sinn
- Vektoren
xundywerden nicht verändert (und sollen auch nicht verändert werden) - Call-by-Reference da sonst beide Vektoren unnötigerweise kopiert werden
- Vektoren
Problem: Fehler, da Compiler nicht weiß, dass die Methoden
get()undsize()die Read-only Referenzen nicht verändern
1 2 3 4 5 6 7 | double scalarProd(const Vector& x, const Vector& y){
double tmp=0;
for(int i=0;i<x.size();++i){
tmp += x.get(i)*y.get(i);
}
return tmp;
}
|
input_line_11:3:19: error: member function 'size' not viable: 'this' argument has type 'const Vector', but function is not marked const
for(int i=0;i<x.size();++i){
^
input_line_10:1:13: note: 'size' declared here
int Vector::size(){
^
input_line_11:4:16: error: member function 'get' not viable: 'this' argument has type 'const Vector', but function is not marked const
tmp += x.get(i)*y.get(i);
^
input_line_9:1:17: note: 'get' declared here
double& Vector::get(int k){
^
input_line_11:4:25: error: member function 'get' not viable: 'this' argument has type 'const Vector', but function is not marked const
tmp += x.get(i)*y.get(i);
^
input_line_9:1:17: note: 'get' declared here
double& Vector::get(int k){
^
Interpreter Error:
Lösung: Methoden als const deklarieren¶
- Einzige Änderung in den Signaturen der Methoden (Zeile 13-15 unten)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | #include <iostream>
#include <vector>
#include <cmath>
using std::vector;
class Vector {
private:
vector<double> coeff;
public:
Vector(int dim=0, double init=0);
double get(int k) const;
int size() const;
double norm() const;
};
|
1 | Vector::Vector(int dim, double init): coeff(dim,init){}
|
1 2 3 | double Vector::get(int k) const{
return coeff[k];
}
|
1 2 3 | int Vector::size() const{
return coeff.size();
}
|
- Der Compiler weiß nun, dass z.B.
x.size()das Objektxnicht verändert. Daher ist die Anwendung auf Read-only Objekte erlaubt (Zeile 3 unten).
1 2 3 4 5 6 7 | double scalarProd(const Vector& x, const Vector& y){
double tmp=0;
for(int i=0;i<x.size();++i){
tmp += x.get(i)*y.get(i);
}
return tmp;
}
|
1 2 3 4 5 | int main(){
Vector x(5,1);
Vector y(5,3);
std::cout << "x*y = " << scalarProd(x,y) << std::endl;
}
|
x*y = 15
Zusammenfassung Syntax¶
bei normalen Datentypen (nicht Pointer)
const intvarint constvar- dieselbe Bedeutung = Integer-Konstante
bei Referenzen
const int&ref = Referenz aufconst intint const&ref Referenz aufconst int
Achtung bei Pointern
const int* ptr= Pointer aufconst intint const* ptr= Pointer aufconst intint* const ptr= konstanter Pointer aufint
bei Methoden, die nur Lese-Zugriff brauchen
ClassName:: fct( ... input ...) const- kann Methode sonst nicht mit
const-Refs nutzen
sinnvoll, falls Rückgabe eine Referenz ist
const int& fct( ... input ...)- lohnt sich nur bei großer Rückgabe, die nur gelesen wird
- Achtung: Rückgabe muss existieren, sonst Laufzeitfehler!
- d.h. Rückgabe sollte Daten der Klasse sein
Überladen und const¶
constwird bei Call-by-Value nicht berücksichtigt
1 2 | void f(int x) { cout << "int\n"; };
void f(const int x) { cout << "const int\n"; }; //Syntax Fehler
|
constwichtig bei Call-by-Reference
1 2 | void f(int& x) { cout << "int\n"; };
void f(const int& x) { cout << "const int\n"; }; // OK da Call-by-Reference
|
Überladen von const-Methoden¶
- kann Methode durch
constMethode überladenconst-Variante wird beiconst-Objekten verwendet, non-const-Variante bei non-const-Objekten
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <iostream>
#include <vector>
using std::vector;
class Vector {
private:
vector<double> coeff;
public:
Vector(int dim=0, double init=0);
double& get(int k);
double get(int k) const;
int size() const;
double norm() const;
};
|
1 | Vector::Vector(int dim, double init): coeff(dim,init){}
|
1 2 3 | double Vector::get(int k) const{
return coeff[k];
}
|
1 2 3 | double& Vector::get(int k){
return coeff[k];
}
|
- In Zeile 4 unten wird die non-
constVersion vonget()aufgerufen, daxvom Typ non-constist - In Zeile 5 unten wird die
constVersion vonget()aufgerufen, dayvom Typconstist
1 2 3 4 5 6 7 | int main(){
Vector x(5,1);
const Vector y(5,1);
x.get(3)=4; //non-const Version of get(), can be used for write access
std::cout << y.get(3); //const Version of get(), only usable for read access
return 0;
}
|
1
Überladen von Operatoren¶
- In C++ kann man vielen Operatoren neue Bedeutungen geben, z.B.
x*yfür Vektoren - Sehr praktisch um mathematischen Code besser lesbar zu machen (näher an der mathematischen Schreibweise)
1 2 3 | #include <iostream>
#include <vector>
using std::vector;
|
1 2 3 4 5 6 7 | double operator*(const std::vector<double>& x, const std::vector<double>& y){
double tmp = 0;
for(int i=0;i<x.size();++i){
tmp +=x[i]*y[i];
}
return tmp;
}
|
- Read-only Referenzen in Zeile 1 oben sinnvoll da Input nicht verändert wird
1 2 3 4 5 | int main(){
vector<double> x(10,1);
vector<double> y(10,2);
std::cout << "x*y = " << x*y << std::endl;
}
|
x*y = 20
Skalar x Vektor, Vektor x Skalar¶
- Wenn $x,y\in\mathbb{R}^n$ und $\lambda\in\mathbb{R}$, dann müssen $x\cdot y$, $\lambda x$ und $x \lambda$ extra implementiert werden
1 2 3 | #include <iostream>
#include <vector>
using std::vector;
|
1 2 3 4 5 6 7 | double operator*(const std::vector<double>& x, const std::vector<double>& y){
double tmp = 0;
for(int i=0;i<x.size();++i){
tmp +=x[i]*y[i];
}
return tmp;
}
|
1 2 3 4 5 6 7 | std::vector<double> operator*(double lambda, const std::vector<double>& x){
vector<double> result(x.size());
for(int i=0;i<x.size();++i){
result[i] = x[i]*lambda;
}
return result;
}
|
1 2 3 4 5 6 7 | std::vector<double> operator*(const std::vector<double>& x, double lambda){
vector<double> result(x.size());
for(int i=0;i<x.size();++i){
result[i] = x[i]*lambda;
}
return result;
}
|
1 2 3 4 5 6 7 | int main(){
vector<double> x(5,1);
vector<double> y(5,1);
y = 3.14*x*10;
std::cout << "(3.14*x*10)*x = " << x*y << std::endl;
return 0;
}
|
(3.14*x*10)*x = 157
Weiteres Beispiel: Addition für Vektoren¶
1 2 3 | #include <iostream>
#include <vector>
using std::vector;
|
1 2 3 4 5 6 7 | std::vector<double> operator+(const std::vector<double>& x, const std::vector<double>& y){
std::vector<double> result(x.size());
for(int i=0;i<x.size();++i){
result[i]=x[i]+y[i];
}
return result;
}
|
1 2 3 4 5 6 7 8 9 10 | int main(){
vector<double> x(10,1);
vector<double> y(10,2);
x = x + y;
std::cout << "x = (";
for(int i =0; i<x.size();++i){
std::cout<< x[i] << " ";
}
std::cout << ")" << std::endl;
}
|
x = (3 3 3 3 3 3 3 3 3 3 )
Beispiel für unäre Operatoren: negatives Vorzeichen¶
1 2 3 | #include <iostream>
#include <vector>
using std::vector;
|
- Hier wird das negative Vorzeichen überladen
-x, daher nur ein Input-Parameter
1 2 3 4 5 6 7 | std::vector<double> operator-(const std::vector<double>& x) {
std::vector<double> result(x.size());
for(int i=0;i<x.size();++i){
result[i]=-x[i];
}
return result;
}
|
- Hier wird die Subtraktion überladen
x-y, daher 2 Input-Parameter
1 2 3 4 5 6 7 | std::vector<double> operator-(const std::vector<double>& x, const std::vector<double>& y){
std::vector<double> result(x.size());
for(int i=0;i<x.size();++i){
result[i]=x[i]-y[i];
}
return result;
}
|
1 2 3 4 5 6 7 8 9 10 11 | int main(){
vector<double> x(10,1);
vector<double> y(10,2);
x = x - y;
x = - x;
std::cout << "x = (";
for(int i =0; i<x.size();++i){
std::cout<< x[i] << " ";
}
std::cout << ")" << std::endl;
}
|
x = (1 1 1 1 1 1 1 1 1 1 )
Beispiel für unäre Operatoren als Teil der Klasse¶
- Nur bei benutzerdefinierten Klassen möglich
- Praktisch ist z.B. das Überladen des [ ]-Operators für die Vektor Klasse
- Man kann analog auch den ( )-Operator überladen
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <iostream>
#include <vector>
using std::vector;
class Vector {
private:
vector<double> coeff;
public:
Vector(int dim=0, double init=0);
Vector operator-() const;
double& operator[](int i);
double operator[](int i) const;
int size() const;
};
|
1 | Vector::Vector(int dim, double init): coeff(dim,init){}
|
1 2 3 | int Vector::size() const{
return coeff.size();
}
|
1 2 3 | double& Vector::operator[](int i){
return coeff[i];
}
|
- Um den [ ]-Operator auch auf konstante Objekte anwenden zu können überladen wir den Operator ein zweites Mal.
- Es wird keine Referenz zurückgegeben, daher nur Lesezugriff (alternativ auch
const double&als Rückgabewert)
1 2 3 | double Vector::operator[](int i) const{
return coeff[i];
}
|
1 2 3 4 5 6 7 8 | Vector Vector::operator-() const {
int dim = coeff.size();
Vector result(dim);
for(int i=0;i<dim;++i){
result[i]=-coeff[i];
}
return result;
}
|
1 2 3 4 5 6 7 8 9 10 11 | int main(){
Vector x(10,1);
const Vector y(10,2);
std::cout << "y[3] = " << y[3] << std::endl; //Would not work without const-Version of operator[]
x = - x;
std::cout << "x = (";
for(int i =0; i<x.size();++i){
std::cout<< x[i] << " ";
}
std::cout << ")" << std::endl;
}
|
y[3] = 2 x = (-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 )
Stream Operator << überladen¶
cout-Ausgabe erfolgt über Klassestd::ostreamweitere Ausgabe wird einfach angehängt mit
<<- kann insbesondere
for-Schleife verwenden, um Vektoren/Matrizen mitcoutauszugeben
- kann insbesondere
1 2 3 4 5 6 7 8 9 | std::ostream& operator<<(std::ostream& output,
const Vector& x) {
output << "(";
for(int i=0;i<x.size()-1;++i){
output << x[i] << ", ";
}
output << x[x.size()-1] << ")";
return output;
}
|
1 2 3 4 5 6 7 | int main(){
Vector x(10,1);
const Vector y(10,2);
std::cout << "y[3] = " << y[3] << std::endl; //Would not work without const-Version of operator[]
x = - x;
std::cout << "x = " << x << std::endl;
}
|
y[3] = 2 x = (-1, -1, -1, -1, -1, -1, -1, -1, -1, -1)
Typecast¶
- Ziel: Wir wollen
double-Variablen mit Vektoren der Länge 1 vom TypVectoridentifizieren - Lässt sich durch Typecast und geeigneten Konstruktoren erreichen
- Wir vertauschen die Argumente im Konstruktor um den Aufruf
Vector x(3.14);zu erlauben - Wir implementieren den Typecast operator
- Wir vertauschen die Argumente im Konstruktor um den Aufruf
1 2 3 4 5 6 7 8 9 10 11 12 | #include <iostream>
#include <vector>
using std::vector;
class Vector {
private:
vector<double> coeff;
public:
Vector(double init=0, int dim=1);
operator double() const;
};
|
1 | Vector::Vector(double init, int dim): coeff(dim,init){}
|
1 2 3 4 5 6 7 8 9 10 11 12 | Vector::operator double() const {
try{
if(coeff.size()==1){
return coeff[0];
}
throw coeff.size();
}
catch(int n){
std::cout << "Vectors of length " << n << " can't be converted to double" << std::endl;
std::abort();
}
}
|
Zeile 2 unten: Der (automatisch generierte) Kopierkonstruktor von
Vectorwird aufgerufen und die rechte Seite4.13wird aufVectorgecasted. Dafür wird der KonstruktorVector(4.13)mit Default Parameterdim=1verwendet.Zeile 3 unten:
vwird implizit aufdoublegecasted. Dafür wird der Typecast operator (oben) verwendet
1 2 3 4 5 6 | int main(){
Vector v = 4.13;
double x = v;
std::cout << "x = " << x;
return 0;
}
|
Zusammenfassung der Syntax¶
Konstruktor (= Type Cast auf
Class)Class::Class( ... input ... )
Destruktor
Class::~Class()
Type Cast von
ClassauftypeClass::operator type() const- explizit durch Voranstellen
(type) - implizit bei Zuweisung auf Variable vom Typ
type
Kopierkonstruktor (Deklaration mit Initialisierung)
Class::Class(const Class&)- expliziter Aufruf durch
Class var(rhs);- oder
Class var = rhs;
- oder
- implizit bei Funktionsaufruf (Call by Value)
Zuweisungsoperator
Class& Class::operator=(const Class&)
unäre Operatoren, z.B. Tilde
~und Vorzeichen-const Class Class::operator-() const
binäre Operatoren, z.B.
+,-,*,/- `const Class operator+(const Class&, const Class&)
- außerhalb der Klasse als Funktion
Ausgabe mittels
coutstd::ostream& operator<<(std::ostream& output, const Class& object)
Welche Operatoren kann man überladen?¶
+ , -- , * , / , , , ^ , %
|, ~ , ! , = , < , > , +=
-=, *= , /= , %= , ^= , &= , |=
<< , >> , >>= , <<= , == , !=, <=
>= , && , || , ++ , -- , ->* , ,
-> , [], () , new , new[] , delete , delete[]
++als unärer Operator, vorangestellt++ varconst Class Class::operator++()
++als unärer Operator, nachgestelltvar ++const Class Class::operator++(int)
+als binärer Operatorconst Class operator+(const Class&, const Class&)- oder
const Class Class::operator+(const Class&)
kann Operatoren auch überladen
- z.B. Division
Complex/doublevs.Complex/Complex - z.B. unär und binär (neg. Vorzeichen vs. Minus)
- unterschiedliche Signatur beachten!
- z.B. Division
Man kann keine neuen Operatoren definieren!
Man kann
.,:,::,sizeof,.*nicht überladen!Im Test sind Signaturen für Operator vorgegeben!
- Ausnahme: Konstruktor, Destruktor!
Dynamische Speicherverwaltung in C++¶
- Tipp: Wenn möglich
std::vector-Template verwenden (oder andere Container Klasse)- Vorteil: Automatische Speicherverwaltung
- Manuelle Speicherverwaltung in C++ ist mit
malloc,realloc,freegenauso wie in C möglich- Bibliothek
<cstdlib>einbinden nicht vergessen!
- Bibliothek
Neue Befehle:
new,new[],delete,delete[]mallocreserviert nur Speicher- Nachteil: Konstruktor wird nicht aufgerufen
- d.h. Initialisierung händisch
ein dynamisches Objekt
type* var = (type*) malloc(sizeof(type));type* var = ...;
dynamischer Vektor von Objekten der Länge
Ntype* vec = (type*) malloc(N*sizeof(type));vec[j] = ...;
in C++ ist Type Cast bei
malloczwingend!newreserviert Speicher + ruft Konstruktoren aufein dynamisches Objekt (mit Standardkonstruktor)
type* var = new type;
ein dynamisches Objekt (mit Konstruktor)
type* var = new type(... input ... );
dyn. Vektor der Länge
N(mit Standardkonstruktor)type* vec = new type[N];- Standardkonstruktor für jeden Koeffizienten
Im Test:
new,malloc,std::vector, aber konsistent! (wenn nicht explizit angegeben)
delete vs. free¶
freegibt Speicher vonmallocfreitype* vec = (type*) malloc(N*sizeof(type));free(vec);- unabhängig von Objekt / Vektor von Objekten
- nur auf Output von
mallocanwenden!
deleteruft Destruktor auf und gibt Speicher vonnewfreitype* var = new type(... input ... );delete var;- für ein dynamisch erzeugtes Objekt
- nur auf Output von
newanwenden!
delete[]ruft Destruktor für jeden Koeffizienten auf und gibt Speicher vonnew ...[N]freitype* vec = new type[N];delete[] vec;- für einen dynamischen Vektor von Objekten
- nur auf Output von
new ...[N]anwenden!
Konvention: Falls Pointer auf keinen dynamischen Speicher zeigt, wird er händisch auf
NULLgesetzt- d.h. nach
free,delete,delete[]folgt vec = (type*) NULL;- in C++ häufiger:
vec = (type*) 0;
- d.h. nach
Negativ Beispiel: Vektor ohne std::vector¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | #include <iostream>
class Vector {
private:
double* coeff;
int dim;
public:
Vector(){
coeff= (double*)0;
dim = 0;
}
Vector(int dim, double init);
Vector(const Vector& input);
Vector& tmp(const Vector& input);
~Vector();
double& get(int j){
return coeff[j];
}
double get(int j) const{
return coeff[j];
}
int size() const{
return dim;
}
};
|
- Konstruktor mit Parametern
1 2 3 4 5 6 7 8 | Vector::Vector(int dim, double init){
std::cout << "Constructor" << std::endl;
coeff = new double[dim];
this->dim = dim;
for(int i=0;i<dim;++i){
coeff[i]=init;
}
}
|
- Kopierkonstruktor
1 2 3 4 5 6 7 8 | Vector(const Vector& input){
std::cout << "Copy-Constructor" << std::endl;
coeff = new double[input.size()];
for(int i=0;i<input.size();++i){
coeff[i]=input.get(i);
}
dim = input.size();
}
|
- Zuweisungsoperator
- Muss Speicher freigeben, falls dieser schon existiert
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | Vector& operator=(const Vector& input) {
std::cout << "Assignement Operator" << std::endl;
if (this != &input) {
if(coeff!=(double*)0){
delete[] coeff;
}
coeff = new double[input.size()];
dim = input.size();
for(int i=0;i<input.size();++i){
coeff[i]=input.get(i);
}
}
return *this;
}
|
- Destruktor muss Speicher freigeben (sonst Speicherleck)
1 2 3 4 5 6 | ~Vector(){
std::cout << "Destructor" << std::endl;
if(coeff!=(double*)0){
delete[] coeff;
}
}
|
- Die großen Drei
- Destruktor
- Zuweisungsoperator
- Kopierkonstruktor
- Bei dynamischem Speicher müssen immer alle drei implementiert werden, sonst funktioniert der Code mit hoher Wahrscheinlichkeit nicht.
- Ohne Kopierkonstruktor: in Zeile 3 (unten) erfolgt nur Shallow-Copy und am Programmende wird der selbe Speicher von
xundy2 x freigegeben. - Ohne Zuweisungsoperator: in Zeile 5 (unten) erfolgt nur Shallow-Copy und am Programmende wird der selbe Speicher von
xundy2 x freigegeben. - Ohne Destruktor: Der Speicher wird nicht freigegeben
- Ohne Kopierkonstruktor: in Zeile 3 (unten) erfolgt nur Shallow-Copy und am Programmende wird der selbe Speicher von
1 2 3 4 5 6 7 | int main(){
Vector x(3,2);
Vector y = x;
y.get(2) = 0;
x=y;
return 0;
}
|
Constructor Copy-Constructor Assignement Operator Destructor Destructor
Vererbung in C++¶
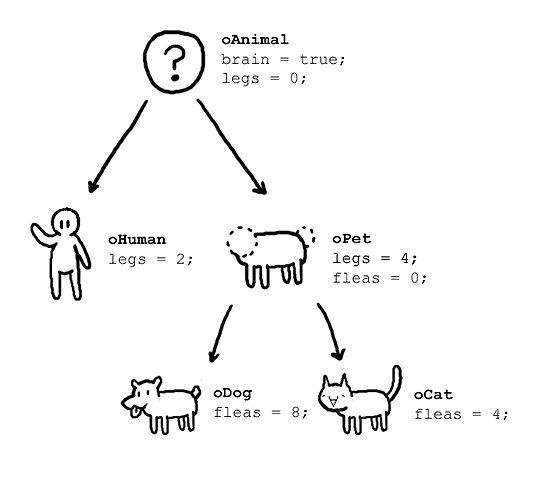
im Alltag werden Objekte klassifiziert, z.B.
- Jede Katze ist ein Haustier
- Hat Grundlegende Eigenschaften eines Haustiers, aber noch mehr
- Jedes Haustier ist ein Tier
- Auch jeder Mensch ist ein Tier
- Jede Katze ist ein Haustier
in C++ mittels Klassen abgebildet
- Klasse (Tier) vererbt alle Members/Methoden an abgeleitete Klasse (Haustier)
- abgeleitete Klasse (Haustier) kann zusätzliche Members/Methoden haben
mathematisches Beispiel: $\mathbb{Q}\subset\mathbb{R}\subset\mathbb{C}$
- Jeder Vektor ist auch eine Matrix, jedes Quadrat ist ein Polygon, usw...
Bild oben von https://patrickgoudjoako.com/2014/06/25/inherit-when-inheritance-simplifies-the-design/
public-Vererbung¶
class Child: public Parent { ... };Klasse
Childerbt alles vonParent- alle Members + Methoden
Qualifier
publicgibt Art der Vererbung an- alle
privateMembers vonParentsind unsichtbare Members vonChild, d.h. nicht im Scope! - alle
publicMembers vonParentsind auchpublicMembers vonChild
- alle
später noch Qualifier
privateundprotectedkann weitere Members + Methoden zusätzlich für
Childim Block{...}definieren wie bisher!
Vorteil bei Vererbung:
- Muss Funktionalität ggf. 1x implementieren!
- Code wird kürzer (vermeidet Copy'n'Paste)
- Fehlervermeidung
Formales Beispiel¶

class Animal { ... };class Human: public Animal { ... };class Pet: public Animal { ... };class Dog: public Pet { ... };class Cat: public Pet { ... };
Ein erstes C++ Beispiel¶
1 2 3 4 5 6 7 8 9 10 | #include <iostream>
using std::cout;
class Parent {
private:
double x;
public:
double getX() const { return x; }
void setX(double input) { x = input; }
};
|
1 2 3 4 5 6 7 | class Child : public Parent {
private:
double y;
public:
double getY() const { return y; }
void setY(double input) { y = input; }
};
|
1 2 3 4 5 6 7 8 9 10 11 12 13 | int main() {
Parent var1;
Child var2;
var1.setX(5);
cout << "var1.x = " << var1.getX() << "\n";
var2.setX(1);
var2.setY(2);
cout << "var2.x = " << var2.getX() << "\n";
cout << "var2.y = " << var2.getY() << "\n";
return 0;
}
|
var1.x = 5 var2.x = 1 var2.y = 2
private Members vererben 1/2¶
1 2 3 4 5 6 7 8 9 10 11 12 | #include <iostream>
using std::cout;
class Parent {
private:
double x;
public:
Parent() { x = 0; }
Parent(double inx) { x = inx; }
double getX() const { return x; }
void setX(double inx) { x = inx; }
};
|
- derselbe Syntax-Fehler in Zeile 5 & 6 unten:
- Zugriff auf
privateMembers nur in eigener Klasse, nicht im Scope bei Objekten abgeleiteter Klassen
- Zugriff auf
1 2 3 4 5 6 7 8 9 | class Child : public Parent {
private:
double y;
public:
Child() { x = 0; y = 0; };
Child(double inx, double iny) { x = inx; y = iny; };
double getY() const { return y; }
void setY(double iny) { y = iny; }
};
|
input_line_9:5:13: error: 'x' is a private member of 'Parent'
Child() { x = 0; y = 0; };
^
input_line_8:5:10: note: declared private here
double x;
^
input_line_9:6:35: error: 'x' is a private member of 'Parent'
Child(double inx, double iny) { x = inx; y = iny; };
^
input_line_8:5:10: note: declared private here
double x;
^
Interpreter Error:
private Members vererben 2/2¶
- Lösung: Verwende den Konstruktor oder die Zugriffsfunktionen von
Parent xist inChildnicht im Scope, aber existiert!
1 2 3 4 5 6 7 8 9 10 11 12 | #include <iostream>
using std::cout;
class Parent {
private:
double x;
public:
Parent() { x = 0; }
Parent(double inx) { x = inx; }
double getX() const { return x; }
void setX(double inx) { x = inx; }
};
|
1 2 3 4 5 6 7 8 9 | class Child : public Parent {
private:
double y;
public:
Child() { setX(0); y = 0; };
Child(double inx, double iny) {setX(inx); y = iny;};
double getY() const { return y; }
void setY(double iny) { y = iny; }
};
|
1 2 3 4 5 6 7 8 | int main() {
Parent var1(5);
Child var2(1,2);
cout << "var1.x = " << var1.getX() << ", ";
cout << "var2.x = " << var2.getX() << ", ";
cout << "var2.y = " << var2.getY() << "\n";
return 0;
}
|
var1.x = 5, var2.x = 1, var2.y = 2
Konstruktor & Destruktor 1/2¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | #include <iostream>
using std::cout;
class Parent {
private:
double x;
public:
Parent() {
cout << "Parent()\n";
x = 0;
}
Parent(double inx) {
cout << "Parent(" << inx << ")\n";
x = inx;
}
~Parent() {
cout << "~Parent()\n";
}
double getX() const { return x; }
void setX(double inx) { x = inx; }
};
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | class Child : public Parent {
private:
double y;
public:
Child() {
cout << "Child()\n";
setX(0);
y = 0;
};
Child(double inx, double iny) {
cout << "Child(" << inx << "," << iny << ")\n";
setX(inx);
y = iny;
};
~Child() {
cout << "~Child()\n";
}
double getY() const { return y; }
void setY(double iny) { y = iny; }
};
|
- Anlegen eines Objekts vom Typ
Childruft Konstruktoren vonParentundChildauf- automatisch wird Standard-Konstruktor aufgerufen!
- Freigabe eines Objekts vom Typ
Childruft Destruktoren vonChildundParent
1 2 3 4 5 6 7 8 | int main() {
Parent var1(5);
Child var2(1,2);
cout << "var1.x = " << var1.getX() << ", ";
cout << "var2.x = " << var2.getX() << ", ";
cout << "var2.y = " << var2.getY() << "\n";
return 0;
}
|
Child(1,2) var1.x = 5, var2.x = 1, var2.y = 2 ~Child() ~Parent() ~Parent()
Konstruktor & Destruktor 2/2¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | #include <iostream>
using std::cout;
class Parent {
private:
double x;
public:
Parent() {
cout << "Parent()\n";
x = 0;
}
Parent(double inx) {
cout << "Parent(" << inx << ")\n";
x = inx;
}
~Parent() {
cout << "~Parent()\n";
}
double getX() const { return x; }
void setX(double inx) { x = inx; }
};
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | class Child : public Parent {
private:
double y;
public:
Child() {
cout << "Child()\n";
setX(0);
y = 0;
};
Child(double inx, double iny) : Parent(inx) {
cout << "Child(" << inx << "," << iny << ")\n";
y = iny;
};
~Child() {
cout << "~Child()\n";
}
double getY() const { return y; }
void setY(double iny) { y = iny; }
};
|
- kann bewusst Konstruktor von
Parentwählen wenn Konstruktor vonChildaufgerufen wirdChild(...) : Parent(...) {... };- ruft Konstruktor von
Parent, welcher der Signatur entspricht ($\to$ Überladen)
1 2 3 4 5 6 7 8 | int main() {
Parent var1(5);
Child var2(1,2);
cout << "var1.x = " << var1.getX() << ", ";
cout << "var2.x = " << var2.getX() << ", ";
cout << "var2.y = " << var2.getY() << "\n";
return 0;
}
|
Parent(5) Parent(1) Child(1,2) var1.x = 5, var2.x = 1, var2.y = 2 ~Child() ~Parent() ~Parent()
Eine Klasse für Polygone¶
- Polygone sind 2D-Figuren die aus endlich vielen Geradenabschnitten bestehen. Alle Geraden sind miteinander verbunden und erzeugen eine geschlossene Kurve.
- Ein Polygon ist eindeutig definiert durch alle seine Eckpunkte in $\mathbb{R}^2$ und deren Reihenfolge
1 2 3 4 5 6 7 8 9 10 11 12 13 | #include <iostream>
#include <vector>
#include <cmath>
using std::vector;
class Polygon {
private:
vector<vector<double> > nodes;
public:
Polygon(int n=0);
int size(){ return nodes.size();};
double length();
vector<double>& getNode(int j);
};
|
- Eine sinnvolle Methode wäre z.B. auch der Flächeninhalt. Für allgemeine Polygone ist dieser aber nicht einfach zu bestimmen
1 | Polygon::Polygon(int n): nodes(n,vector<double>(2,0)){}
|
1 2 3 4 5 6 7 8 9 10 11 12 | double Polygon::length(){
double tmp=0, dx, dy;
for(int i=0;i<size()-1;++i){
dx = nodes[i+1][0]-nodes[i][0];
dy = nodes[i+1][1]-nodes[i][1];
tmp += sqrt(dx*dx + dy*dy);
}
dx = nodes[0][0]-nodes[size()-1][0];
dy = nodes[0][1]-nodes[size()-1][1];
tmp += sqrt(dx*dx + dy*dy);
return tmp;
}
|
1 2 3 | vector<double>& Polygon::getNode(int j){
return nodes[j];
}
|
std::vectorerlaubt auch direkte Initialisierung wie bei statischen Arrays (Zeilen 3-5 unten)
1 2 3 4 5 6 7 | int main(){
Polygon P(3);
P.getNode(0) = vector<double>{0,0};
P.getNode(1) = vector<double>{1,0};
P.getNode(2) = vector<double>{0,1};
std::cout << "Length = " << P.length();
}
|
Length = 3.41421
Dreiecksklasse abgeleitet von der Polygonklasse¶
- Ein Dreieck hat alle Eigenschaften eines Polygons, kann aber mehr (z.B. einfache Flächenformel)
1 2 3 4 5 | class Triangle: public Polygon {
public:
Triangle();
double area();
};
|
1 | Triangle::Triangle(): Polygon(3){}
|
1 2 3 4 5 6 7 | double Triangle::area(){
double ax = getNode(1)[0]-getNode(0)[0];
double ay = getNode(1)[1]-getNode(0)[1];
double bx = getNode(2)[0]-getNode(0)[0];
double by = getNode(2)[1]-getNode(0)[1];
return 0.5*fabs(ax*by - ay*bx);
}
|
1 2 3 4 5 6 7 8 | int main(){
Triangle T;
T.getNode(0) = vector<double>{0,0};
T.getNode(1) = vector<double>{1,0};
T.getNode(2) = vector<double>{0,1};
std::cout << "Length = " << T.length() << ", Area = " << T.area() << std::endl;
return 0;
}
|
Length = 3.41421, Area = 0.5
Methoden redefinieren 1/2¶
- wird in Basisklasse und abgeleiteter Klasse eine Methode gleichen Namens definiert, so steht für Objekte der abgeleiteten Klasse nur diese Methode zur Verfügung, alle Überladungen in der Basis- klasse werden überdeckt, sog. Redefinieren
1 2 3 4 5 6 7 8 | #include <iostream>
using std::cout;
class Parent {
public:
void print() { cout << "no input\n"; }
void print(int x) { cout << "input = " << x << "\n"; }
};
|
Unterscheide:
- Überladen (Zeile 6 + 7 oben)
- und Redefinieren (Zeile 3 unten)
1 2 3 4 | class Child : public Parent {
public:
void print() { cout << "Child: no input\n"; }
};
|
Komplilieren liefert Fehler, da in Child alle Versionen von print die in Parent deklariert wurden überdeckt sind.
1 2 3 4 5 6 7 8 9 10 | int main() {
Parent var1;
Child var2;
var1.print();
var1.print(1);
var2.print();
var2.print(2);
return 0;
}
|
input_line_10:7:8: error: too many arguments to function call, expected 0, have 1; did you mean 'Parent::print'?
var2.print(2);
^~~~~
Parent::print
input_line_8:6:8: note: 'Parent::print' declared here
void print(int x) { cout << "input = " << x << "\n"; }
^
Interpreter Error:
Methoden redefinieren 2/2¶
Parenthat überladene Methodenprint()undprint(int x)Childhat nur eine Methodeprint()printausParentüberdeckt (Redefinition)
- Zugriff auf
printaus Basisklasse über vollständigen Namen möglich (inkl. Klasse als Namensbereich), siehe Zeile 8 (unten)
1 2 3 4 5 6 7 8 9 10 | int main() {
Parent var1;
Child var2;
var1.print();
var1.print(1);
var2.print();
var2.Parent::print(2); // only change in this line
return 0;
}
|
no input input = 1 Child: no input input = 2
Achsenparalleles Rechteck: abgeleitet von der Polygonklasse¶
1 2 3 4 5 6 7 | class Quad: public Polygon {
public:
Quad();
double area();
double length();
vector<Triangle> decompose();
};
|
- Wir speichern nur den linken unteren und den rechten oberen Eckpunkt
- Daher müssen wir die Methode
length()redefinieren
1 | Quad::Quad(): Polygon(2){}
|
1 2 3 4 5 6 7 8 9 10 11 12 | vector<Triangle> Quad::decompose(){
vector<Triangle> ret(2);
ret[0].getNode(0) = getNode(0);
ret[0].getNode(2) = getNode(1);
ret[0].getNode(1)[0] = getNode(0)[0];
ret[0].getNode(1)[1] = getNode(1)[1];
ret[1].getNode(0) = getNode(0);
ret[1].getNode(2) = getNode(1);
ret[1].getNode(1)[0] = getNode(1)[0];
ret[1].getNode(1)[1] = getNode(0)[1];
return ret;
}
|
1 2 3 4 | double Quad::area(){
vector<Triangle> Ts = decompose();
return Ts[0].area()+ Ts[1].area();
}
|
1 2 3 | double Quad::length(){
return 2*(getNode(1)[0]-getNode(0)[0]) + 2*(getNode(1)[1]-getNode(0)[1]);
}
|
1 2 3 4 5 6 7 8 9 | int main(){
Quad Q;
Q.getNode(0) = vector<double>{0,0};
Q.getNode(1) = vector<double>{1,1};
std::cout << "Length = " << Q.length() << ", Area = " << Q.area() << std::endl;
std::cout << "Polygon::length() = " << Q.Polygon::length() << std::endl;
return 0;
}
|
Length = 4, Area = 1 Polygon::length() = 2.82843
Anwendung: Finite-Element-Methode¶
- Genaueres in Numerik von Partiellen Differentialgleichungen
- Grob: Um schwierige Differentialgleichungen zu lösen zerlegt man das Gebiet auf dem die Gleichung gestellt ist in kleine Dreiecke (oder andere Polygone).
- Diese Zerlegung nennt man Gitter (in Englisch: Mesh oder Triangulation)
- Für jedes Element (jedes Dreieck) muss man irgendwann die Fläche und andere ähnliche Dinge berechnen.
private, protected, public 1/2¶
private,protected,publicsind Qualifier für Members in Klassen- kontrollieren, wie auf Members der Klasse zugegriffen werden darf
private(Standard)- Zugriff nur von Methoden der gleichen Klasse
protected- Zugriff nur von Methoden der gleichen Klasse
- Unterschied zu
privatenur bei Vererbung
public- erlaubt Zugriff von überall
Konvention: Datenfelder sind immer
private
private, protected, public sind auch Qualifier
für Vererbung:
- class
Child : public Parent ...
member in Parent: |
public |
protected |
private |
|---|---|---|---|
Sichtbarkeit in Child: |
public |
protected |
hidden |
- class
Child : protected Parent ...
member in Parent: |
public |
protected |
private |
|---|---|---|---|
Sichtbarkeit in Child: |
protected |
protected |
hidden |
- class
Child : private Parent ...
member in Parent: |
public |
protected |
private |
|---|---|---|---|
Sichtbarkeit in Child: |
private |
private |
hidden |
Sichtbarkeit ändert sich durch Art der Vererbung
- Zugriff kann nur verschärft werden
- andere außer
publicmachen selten Sinn
Wichtig: protected members sind wie private members, nur sind sie in abgeleiteten Klassen noch sichtbar
private, protected, public 2/2¶
- Compiler liefert Syntax-Fehler
1 2 3 4 5 6 7 8 9 | #include <iostream>
class Parent {
private:
int a;
protected:
int b;
public:
int c;
};
|
1 2 3 4 5 6 7 8 | class Child : public Parent {
public:
void method() {
a = 10; // not OK as a is hidden
b = 10; // OK as b is protected
c = 10; // OK as c is public
}
};
|
input_line_31:4:5: error: 'a' is a private member of '__cling_N523::Parent'
a = 10; // not OK as a is hidden
^
input_line_30:3:7: note: declared private here
int a;
^
Interpreter Error:
1 2 3 4 5 6 7 8 9 10 11 12 13 | int main() {
Parent parent;
parent.a = 10; // not OK as a is private
parent.b = 10; // not Ok as b is protected
parent.c = 10; // OK as c is public
Child child;
child.a = 10; // not OK as a is hidden
child.b = 10; // not OK as b is protected
child.c = 10; // OK as c is public
return 0;
}
|
input_line_32:3:10: error: 'a' is a private member of '__cling_N523::Parent'
parent.a = 10; // not OK as a is private
^
input_line_30:3:7: note: declared private here
int a;
^
input_line_32:4:10: error: 'b' is a protected member of '__cling_N523::Parent'
parent.b = 10; // not Ok as b is protected
^
input_line_30:5:7: note: declared protected here
int b;
^
input_line_32:6:3: error: unknown type name 'Child'
Child child;
^
Interpreter Error:
Polymorphie¶
Jedes Objekt der abgeleiteten Klasse ist auch ein Objekt der Basisklasse
- Vererbung impliziert immer ist-ein-Beziehung
Jede Klasse definiert einen Datentyp
Objekte können mehrere Typen haben
Objekte abgeleiteter Klassen haben mindestens zwei Datentypen:
- Typ der abgeleiteten Klasse
- und Typ der Basisklasse
kann den jeweils passenden Typ verwenden
- Diese Eigenschaft nennt man Polymorphie (griechisch für Vielgestaltigkeit)
Das hat insbesondere Konsequenzen für Pointer!
Pointer und virtual 1/3¶
1 2 3 4 5 6 7 | #include <iostream>
using std::cout;
class Parent {
public:
void print() {cout << "Parent\n";}
};
|
1 2 3 4 | class Child : public Parent {
public:
void print() {cout << "Child\n";}
};
|
- Zeile 2 unten: Objekt
avom TypChildist auch vom TypParent - Pointer auf
Parentmit Adresse vonamöglich - Zeile 6 unten ruft
printausParentauf- i.a. soll
printausChildverwendet werden
- i.a. soll
1 2 3 4 5 6 7 8 | int main() {
Child a;
Child* pA = &a;
Parent* pB = &a;
pA->print();
pB->print();
return 0;
}
|
Child Parent
Pointer und virtual 2/3¶
1 2 3 4 5 6 7 | #include <iostream>
using std::cout;
class Parent {
public:
virtual void print() {cout << "Parent\n";}
};
|
1 2 3 4 | class Child : public Parent {
public:
void print() {cout << "Child\n";}
};
|
- Zeile 6 oben: neues Schlüsselwort
virtual- vor Signatur der Methode
print(in Basisklasse!) - deklariert virtuelle Methode
- zur Laufzeit wird korrekte Methode aufgerufen
- Varianten müssen gleiche Signatur haben
- Zeile 19 ruft nun redefinierte Methode
printauf
- vor Signatur der Methode
1 2 3 4 5 6 7 8 | int main() {
Child a;
Child* pA = &a;
Parent* pB = &a;
pA->print();
pB->print();
return 0;
}
|
Child Child
Pointer und virtual 3/3¶
1 2 3 4 | class Child1 : public Parent {
public:
void print() {cout << "Child1\n";}
};
|
1 2 3 4 | class Child2 : public Parent {
public:
void print() {cout << "Child2\n";}
};
|
varist Array von Objekten mit verschiedenen Typen
1 2 3 4 5 6 7 8 9 10 | int main() {
Parent* var[2];
var[0] = new Child1;
var[1] = new Child2;
for (int j=0; j<2; ++j) {
var[j]->print();
}
return 0;
}
|
Child1 Child2
Destruktor und virtual 1/2¶
- Destruktor von
Childwird nicht aufgerufen!- ggf. entsteht toter Speicher, falls
Childzusätzlichen dynamischen Speicher anlegt
- ggf. entsteht toter Speicher, falls
- Destruktoren werden deshalb üblicherweise als virtual deklariert
1 2 3 4 5 6 7 8 9 | #include <iostream>
using std::cout;
class Parent {
public:
~Parent() {
cout << "~Parent()\n";
}
};
|
1 2 3 4 5 6 | class Child : public Parent {
public:
~Child() {
cout << "~Child()\n";
}
};
|
1 2 3 4 5 | int main() {
Parent* var = new Child;
delete var;
return 0;
}
|
~Parent()
Destruktor und virtual 2/2¶
- Destruktor von
Childwird aufgerufen- ruft implizit Destruktor von
Parentauf
- ruft implizit Destruktor von
1 2 3 4 5 6 7 8 9 | #include <iostream>
using std::cout;
class Parent {
public:
virtual ~Parent() {
cout << "~Parent()\n";
}
};
|
1 2 3 4 5 6 | class Child : public Parent {
public:
~Child() {
cout << "~Child()\n";
}
};
|
1 2 3 4 5 | int main() {
Parent* var = new Child;
delete var;
return 0;
}
|
~Child() ~Parent()
Virtuelle Methoden 1/2¶
- Obwohl
egoredefiniert wird fürChild1, bindetprintimmeregovonParentein
1 2 3 4 5 6 7 8 | #include <iostream>
using std::cout;
class Parent {
public:
void ego() { cout << "Parent\n"; }
void print() { cout << "I am "; ego(); }
};
|
1 2 3 4 | class Child1: public Parent {
public:
void ego() { cout << "Child1\n"; }
};
|
1 | class Child2: public Parent {};
|
1 2 3 4 5 6 7 8 9 | int main() {
Parent var0;
Child1 var1;
Child2 var2;
var0.print();
var1.print();
var2.print();
return 0;
}
|
I am Parent I am Parent I am Parent
Virtuelle Methoden 2/2¶
virtual(Zeile 6) sorgt für korrekte Einbindung, falls diese Methode für abgeleitete Klasse redefiniert ist
1 2 3 4 5 6 7 8 | #include <iostream>
using std::cout;
class Parent {
public:
virtual void ego() { cout << "Parent\n"; }
void print() { cout << "I am "; ego(); }
};
|
1 2 3 4 | class Child1: public Parent {
public:
void ego() { cout << "Child1\n"; }
};
|
1 | class Child2: public Parent {};
|
1 2 3 4 5 6 7 8 9 | int main() {
Parent var0;
Child1 var1;
Child2 var2;
var0.print();
var1.print();
var2.print();
return 0;
}
|
I am Parent I am Child1 I am Parent
Beispiel: Vektor von Dreiecken und Rechtecken (Finite-Element-Mesh)¶

- Wiederholung der Klassen
Polygon,Triangle,Quadmit kleinen Vereinfachungen - Methode
length()istvirtual(Zeile 11), da sie inQuadredefiniert wird
1 2 3 4 5 6 7 8 9 10 11 12 13 | #include <iostream>
#include <vector>
#include <cmath>
using std::vector;
class Polygon {
private:
vector<vector<double> > nodes;
public:
Polygon(int n=0);
int size(){ return nodes.size();};
virtual double length();
vector<double>& getNode(int j);
};
|
1 | Polygon::Polygon(int n): nodes(n,vector<double>(2,0)){}
|
1 2 3 4 5 6 7 8 9 10 11 12 | double Polygon::length(){
double tmp=0, dx, dy;
for(int i=0;i<size()-1;++i){
dx = nodes[i+1][0]-nodes[i][0];
dy = nodes[i+1][1]-nodes[i][1];
tmp += sqrt(dx*dx + dy*dy);
}
dx = nodes[0][0]-nodes[size()-1][0];
dy = nodes[0][1]-nodes[size()-1][1];
tmp += sqrt(dx*dx + dy*dy);
return tmp;
}
|
1 2 3 | vector<double>& Polygon::getNode(int j){
return nodes[j];
}
|
1 2 3 4 5 | class Triangle: public Polygon {
public:
Triangle();
double area();
};
|
1 | Triangle::Triangle(): Polygon(3){}
|
1 2 3 4 5 6 7 | double Triangle::area(){
double ax = getNode(1)[0]-getNode(0)[0];
double ay = getNode(1)[1]-getNode(0)[1];
double bx = getNode(2)[0]-getNode(0)[0];
double by = getNode(2)[1]-getNode(0)[1];
return 0.5*fabs(ax*by - ay*bx);
}
|
1 2 3 4 5 6 | class Quad: public Polygon {
public:
Quad();
double area();
double length();
};
|
1 | Quad::Quad(): Polygon(2){}
|
1 2 3 4 5 | double Quad::area(){
double dx = getNode(1)[0]-getNode(0)[0];
double dy = getNode(1)[1]-getNode(0)[1];
return dx*dy;
}
|
1 2 3 | double Quad::length(){
return 2*(getNode(1)[0]-getNode(0)[0]) + 2*(getNode(1)[1]-getNode(0)[1]);
}
|
- Wir speichern eine Folge von Dreiecken und Rechtecken in einem Vektor
- Da alle
Quads und alleTriangles auchPolygons sind, verwenden wir einen Vektor mit Pointern aufPolygon - Da
length()alsvirtualdeklariert wurde, wird jeweils die richtige Version der Methode aufgerufen
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | int main(){
vector<Polygon*> mesh(2);
mesh[0] = new Quad();
mesh[0]->getNode(0)=vector<double>{0,0};
mesh[0]->getNode(1)=vector<double>{1,1};
mesh[1] = new Triangle();
mesh[1]->getNode(0)=vector<double>{1,0};
mesh[1]->getNode(1)=vector<double>{1,1};
mesh[1]->getNode(2)=vector<double>{2,1};
std::cout << "Length mesh[0] = " << mesh[0]->length() << std::endl;
std::cout << "Length mesh[1] = " << mesh[1]->length() << std::endl;
return 0;
}
|
Length mesh[0] = 4 Length mesh[1] = 3.41421
Beispiel: Gleichungen lösen¶
- In der Mathematik betrachten wir oft Gleichungen vom Typ $$ f(x) = y $$
- $f\colon [a,b]\to\mathbb{R}$ ist eine Funktion und $a,b\in\mathbb{R}$ mit $a<b$
Für $y\in\mathbb{R}$ suchen wir Lösung $x\in [a,b]$
Vererbung bietet sich an, weil:
- Für verschiedene Funktionstypen $f$ gibt es unterschiedlichen Lösungsmethoden
- Bisection, Newton, quadratische Lösungsformel, ...
- Jede Löserklasse soll sich alte Lösungen merken und nicht jedes mal neu berechnen
- Jede Löserklasse speichert Definitionsbereich, Toleranz, ...
- Für verschiedene Funktionstypen $f$ gibt es unterschiedlichen Lösungsmethoden
- Zeile 7: Ein Funktionspointer zeigt auf die Funktion $f$
- Zeile 12: Wir speichern rechte Seiten $y$ und zugehörige Lösungen $x$ im Format $$ ( (x_1, y_1), (x_2, y_2),\ldots) $$
- Zeile 14-15:
private-Methoden die nachschauen ob die Gleichung für eine gegebene rechte Seite schon gelöst wurdelookupund eine Lösung speichert wenn sie neu istaddSol
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | #include <iostream>
#include <vector>
#include <cmath>
using std::vector;
class Solver {
private:
double (*fct)(double);
protected:
double a;
double b;
double tol;
vector<vector<double> > solutions;
double bisection(double a, double b, double rhs, bool& error);
double lookup(double rhs, bool& notfound);
void addSol(double sol, double rhs);
public:
Solver(double (*fct)(double) = NULL, double a=0, double b=0, double tol=1e-13);
void setDomain(double a, double b);
void setTol(double tol);
void setFct(double (*fct)(double));
virtual double eval(double x);
double solve(double rhs);
};
|
1 2 3 4 5 6 7 8 9 10 11 12 13 | void Solver::setDomain(double a, double b){
try{
if(a>b){
throw a;
}
this->a=a;
this->b=b;
}
catch(double x){
std::cout << "Domain boundary invalid" << std::endl;
std::abort();
}
}
|
- Zeile 3: Wenn wir die Funktion $f$ verändern, sind die gespeicherten Lösungen natürlich nicht mehr gültig.
clear()ist eine Methode vonstd::vector, die den Vector auf Länge 0 zurücksetzt.
1 2 3 4 | void Solver::setFct(double (*fct)(double)){
this->fct=fct;
solutions.clear();
}
|
1 2 3 | void Solver::setTol(double tol){
this->tol = tol;
}
|
1 2 | Solver::Solver(double (*fct)(double), double a, double b, double tol):
fct(fct), solutions(0), a(a), b(b), tol(tol){}
|
- Funktionsauswertung $f(x)$: Wir überprüfen mittels
try-throw-catch, ob $x$ im Interval $[a,b]$ liegt.
1 2 3 4 5 6 7 8 9 10 11 12 13 | double Solver::eval(double x){
try{
if(x>b || x<a){
throw x;
}
return fct(x);
}
catch(double x){
std::cout << "Evaluation point outside of domain" << std::endl;
std::abort();
}
}
|
- Der Bisektionsalgorithms ist auf jede stetige Funktion anwendbar (siehe C-Teil der Vorlesung)
- Zusätzlich übergeben wir eine
bool-Variable mit Call-by-Reference um eine Fehlermeldung zurückzugeben, falls das Verfahren keine Nullstelle findet (Zeile 6-8)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | double Solver::bisection(double a, double b, double rhs, bool& error){
std::cout << "running bisection algorithm...";
int counter = 0;
double m = 0, fm=0;
double fa = eval(a)-rhs;
if(fa*(fct(b)-rhs)>0){
error = true;
return 0;
}
while(b-a>2*tol){
counter++;
m = (a+b)/2;
fm = eval(m)-rhs;
if(fa*fm<=0){
b=m;
}else{
a=m;
fa=fm;
}
}
std::cout << "finished after " << counter << " steps" << std::endl;
error = false;
return m;
}
|
- Die Methode
push_backvonstd::vectorhängt ein gegebenes Element an den Vektor hinten dran - Wir verwenden den
std::vector-Konstruktorvector<double>{sol,rhs}um den Vektor (sol,rhs) zu erzeugen
1 2 3 | void Solver::addSol(double sol, double rhs){
solutions.push_back(vector<double>{sol,rhs});
}
|
- Wir verwenden eine range-based
for-Schleife (for-each) um den Lösungsvektor nach passenden rechten Seiten zu durchsuchen.- Falls eine gespeicherte rechte Seite
sol[1]nahe genug (relativ) an der gegebenen rechten Seiterhsliegt, geben wir die gespeicherte Lösung zurück - Falls nicht, wird
notfoundauftruegesetzt
- Falls eine gespeicherte rechte Seite
1 2 3 4 5 6 7 8 9 10 | double Solver::lookup(double rhs, bool& notfound){
for(vector<double> sol : solutions){
if(fabs(rhs-sol[1])< tol*(1+fabs(sol[1]))){
notfound = false;
return sol[0];
}
}
notfound = true;
return 0;
}
|
- Zeile 3: Wir überprüfen zuerst, ob die Gleichung für die gegebene rechte Seite schon gelöst wurde
- Wenn ja, dann enthält
tmpdie Lösung underroristfalse
- Wenn ja, dann enthält
- Zeile 6: Falls die rechte Seite nicht gefunden wurde, verwenden wir den Bisektionsalgorithmus um die Gleichung zu lösen.
- Falls
error==false, dann enthälttmpdie Lösung - Falls
error==true, geben wir eine Fehlermeldung und brechen ab
- Falls
- Zeile 10: Wir speichern die Lösung ab um sie zukünftig wiederverwenden zu können
- Zeile 15-17: Fehlerbehandlung mit Programmabbruch
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | double Solver::solve(double rhs){
bool error;
double tmp = lookup(rhs,error);
try{
if(error){
tmp = bisection(a,b,rhs,error);
if(error){
throw rhs;
}
addSol(tmp,rhs);
}
return tmp;
}
catch(double rhs){
std::cout << "Can't find solution for given rhs = " << rhs << std::endl;
std::abort();
}
}
|
- Wir testen die Klasse anhand der Funktion $f(x) = e^x-3$ und lösen
- $f(x)=0$ mit Lösung $x=\log(3)$
- $f(x)=1$ mit Lösung $x=\log(4)$
1 2 3 | double f(double x){
return exp(x)-3;
}
|
1 2 3 4 5 6 7 8 9 | int main(){
Solver S(f,0,5,1e-12);
double tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << ", |f(x)-0| = " << fabs(S.eval(tmp)-0) << std::endl;
tmp = S.solve(1);
std::cout << "f(x)=1: x = " << tmp << ", |f(x)-1| = " << fabs(S.eval(tmp)-1) << std::endl;
tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << std::endl;
}
|
running bisection algorithm...finished after 42 steps f(x)=0: x = 1.09861, |f(x)-0| = 1.52767e-12 running bisection algorithm...finished after 42 steps f(x)=1: x = 1.38629, |f(x)-1| = 1.34914e-12 f(x)=0: x = 1.09861
Abgeleitete Löserklasse für differenzierbare Funktionen¶
- Falls wir die erste Ableitung von $f$ kennen, steht uns mit dem Newtonverfahren eine deutlich effizientere Lösungsmethode zur Verfügung
- Beim Bisektionsverfahren erhöht sich die Anzahl der korrekten Dezimalstellen ca. alle drei bis vier Bisektionschritte um eins
- Beim Newtonverfahren verdoppelt sich die Anzahl der korrekten Dezimalstellen in jedem Schritt annähernd
- Wir können viel Funktionalität der Klasse
Solverwiederverwenden und leiten daher eine KlasseSolver_DiffvonSolverab- Durch
protectedMembers inSolverkönnen wir in den Methoden vonSolver_Diffaufa,b,tol,fctohne Zugriffsfunktionen zugreifen, schützen diese Variablen aber dennoch vor Zugriff von außen
- Durch
1 2 3 4 5 6 7 8 9 10 11 12 | class Solver_Diff : public Solver{
private:
double (*deriv)(double);
protected:
double newton(double rhs, double x, bool& error);
public:
Solver_Diff(double (*fct)(double) = NULL,double (*deriv)(double) = NULL, double a=0,
double b=0, double tol=1e-13);
void setDeriv(double (*deriv)(double));
virtual double evalDeriv(double x);
double solve(double rhs);
};
|
1 2 3 4 | void Solver_Diff::setDeriv(double (*deriv)(double)){
this->deriv=deriv;
solutions.clear();
}
|
1 2 | Solver_Diff::Solver_Diff(double (*fct)(double),double (*deriv)(double), double a, double b, double tol) :
Solver(fct,a,b,tol), deriv(deriv){}
|
1 2 3 4 5 6 7 8 9 10 11 12 | double Solver_Diff::evalDeriv(double x){
try{
if(x>b || x<a){
throw x;
}
return deriv(x);
}
catch(double x){
std::cout << "Evaluation point outside of domain" << std::endl;
std::abort();
}
}
|
Das Newton-Verfahren benötigt einen Startwert $x_0\in [a,b]$ und iteriert dann die Vorschrift $$ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}\quad n=0,1,2,\ldots $$
Zeile 15: Abbruch mit Fehlermeldung:
- Das Verfahren versagt, falls $f'(x_n) = 0$, in der Praxis aber auch schon früher bei $f'(x_n)\ll f(x_n)$
- Falls $|x_{n+1}-x_n|$ zu klein wird, also sich das Verfahren fest frisst.
- Falls $x_n\not\in[a,b]$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | double Solver_Diff::newton(double rhs, double x0, bool& error){
std::cout << "running Newton algorithm...";
double fx0,dfx0,x;
int counter = 0;
while(1){
counter++;
fx0 = eval(x0)-rhs;
if(fabs(fx0)<tol){
std::cout << "finished after " << counter << " steps" << std::endl;
error =false;
return x0;
}
dfx0 = evalDeriv(x0);
x = x0 - fx0/dfx0;
if(fabs(dfx0)<tol*fabs(fx0) || fabs(x-x0)<tol*fabs(fx0) || x<a || x>b){
std::cout << "failed! " << std::endl;
error = true;
return 0;
}
x0=x;
}
}
|
- Zeile 3: Der Löser sucht wieder zuerst ob die Lösung schon berechnet wurde
- Zeile 6: Falls nicht, versuchen wir das Newtonverfahren, wobei wir den Startpunkt als Mittelpunkt des Intervals wählen
- Zeile 8: Falls das Newtonverfahren eine Fehlermeldung ausgibt, starten wir das Bisektionsverfahren
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | double Solver_Diff::solve(double rhs){
bool error;
double tmp = lookup(rhs,error);
try{
if(error){
tmp = newton(rhs,0.5*(a+b),error);
if(error){
tmp = bisection(a,b,rhs,error);
if(error){
throw rhs;
}
}
addSol(tmp,rhs);
}
return tmp;
}
catch(double rhs){
std::cout << "Can't find solution for given rhs = " << rhs << std::endl;
std::abort();
}
}
|
- Wir demonstrieren den Löser an $f(x)=e^x-3$ und $g(x) = \arctan(x)$
- Zuerst beobachten wir, dass das Newtonverfahren deutlich schneller konvergiert (6 Schritte) als das Bisektionsverfahren vorhin (42 Schritte)
- Wir sehen aber auch, dass das Newtonverfahren manchmal versagt
1 2 3 | double fprime(double x){
return exp(x);
}
|
1 2 3 | double g(double x){
return atan(x);
}
|
1 2 3 | double gprime(double x){
return 1.0/(1+x*x);
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | int main(){
Solver_Diff S(f,fprime,-1,5,1e-12);
std::cout << "** f(x) = exp(x)-3" << std::endl;
double tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << ", |f(x)-0| = " << fabs(S.eval(tmp)-0) << std::endl;
tmp = S.solve(1);
std::cout << "f(x)=1: x = " << tmp << ", |f(x)-1| = " << fabs(S.eval(tmp)-1) << std::endl;
tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << std::endl;
std::cout << "** f(x) = atan(x)" << std::endl;
S.setFct(g);
S.setDeriv(gprime);
tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << ", |f(x)-0| = " << fabs(S.eval(tmp)-0) << std::endl;
tmp = S.solve(1);
std::cout << "f(x)=1: x = " << tmp << ", |f(x)-1| = " << fabs(S.eval(tmp)-1) << std::endl;
tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << std::endl;
return 0;
}
|
** f(x) = exp(x)-3 running Newton algorithm...finished after 6 steps f(x)=0: x = 1.09861, |f(x)-0| = 2.47358e-13 running Newton algorithm...finished after 6 steps f(x)=1: x = 1.38629, |f(x)-1| = 0 f(x)=0: x = 1.09861 ** f(x) = atan(x) running Newton algorithm...failed! running bisection algorithm...finished after 42 steps f(x)=0: x = 4.54747e-13, |f(x)-0| = 4.54747e-13 running Newton algorithm...finished after 6 steps f(x)=1: x = 1.55741, |f(x)-1| = 0 f(x)=0: x = 4.54747e-13
Abgeleitete Klasse für polynomiale Gleichungen¶
$$ f(x)=a_nx^n + a_{n-1}x^{n-1} +\ldots + a_2 x^2 + a_1 x + a_0 = y $$- Vorteil: Kann Ableitung der Funktion automatisiert ausrechnen
Für kleinen Polynomgrad könnte man sogar explizite Lösungsformeln verwenden (hier nicht gemacht)
Zeile 3: Wir definieren ein neues Member, um den Koeffizientenvektor des Polynoms zu speichern
- Die Funktionspointer
fctundderivwerden wir nicht mehr verwenden
- Die Funktionspointer
- Zeile 4: Wir redefinieren die Methode
setDeriv()als private, weil die Ableitung automatisch berechnet wird und von außen nicht verändert werden soll - Zeile 9-10: Wir redefinieren
evalundevalDeriv, weil wir für Polynome die Funktionspointer nicht verwenden
1 2 3 4 5 6 7 8 9 10 11 | class Solver_Poly : public Solver_Diff{
private:
vector<double>coeff;
void setDeriv();
public:
Solver_Poly(vector<double> coeff = vector<double>(0), double a=0, double b=0, double tol=1e-13);
void setFct(vector<double> coeff);
double eval(double x);
double evalDeriv(double x);
};
|
1 2 | Solver_Poly::Solver_Poly(vector<double> coeff , double a, double b, double tol):
Solver_Diff(NULL,NULL,a,b,tol), coeff(coeff){}
|
1 2 3 4 | void Solver_Poly::setFct(vector<double> coeff){
this->coeff = coeff;
solutions.clear();
}
|
Wir verwenden das Horner-Schema um Polynome effizient auszuwerten. Die Idee dahinter ist, dass bei naiver Berechnung von $a_n x^n + a_{n-1}x^{n-1} +\ldots $ oft sehr große Zwischenergebnisse auftreten, was zu großen Rechenfehlern führt. Das Horner-Schema nutzt die äquivalente Darstellung $$ a_nx^n + a_{n-1}x^{n-1} +\ldots + a_2 x^2 + a_1 x + a_0 = ((\ldots ((a_nx + a_{n-1})x + a_{n-2})x + \ldots )x + a_1)x + a_0 $$
- Kann iterativ von innen nach außen berechnet werden
- vermeidet explizite Berechnung von $x^n$
1 2 3 4 5 6 7 8 9 10 11 | double Solver_Poly::eval(double x){
int n = coeff.size();
if(n==0){
return 0;
}
double tmp = coeff[n-1];
for(int i=n-2;i>=0;--i){
tmp = tmp*x + coeff[i];
}
return tmp;
}
|
Für ein Polynom $f(x):=a_nx^n + a_{n-1}x^{n-1} +\ldots + a_2 x^2 + a_1 x + a_0$ ist die Ableitung durch $$ f'(x) = na_nx^{n-1} + (n-1)a_{n-1}x^{n-2} +\ldots + 2a_2 x + a_1 $$ gegeben. Wieder kann das Horner-Schema verwendet werden um die Ableitung auszuwerten.
1 2 3 4 5 6 7 8 9 10 11 | double Solver_Poly::evalDeriv(double x){
int n = coeff.size();
if(n<=1){
return 0;
}
double tmp = (n-1)*coeff[n-1];
for(int i=n-2;i>=1;--i){
tmp = tmp*x + i*coeff[i];
}
return tmp;
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | int main(){
Solver_Poly S(vector<double>{0.5,0,0,1},-3,5,1e-12);
std::cout << "** f(x) = x^3+0.5" << std::endl;
double tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << ", |f(x)-0| = " << fabs(S.eval(tmp)-0) << std::endl;
tmp = S.solve(1);
std::cout << "f(x)=1: x = " << tmp << ", |f(x)-1| = " << fabs(S.eval(tmp)-1) << std::endl;
tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << std::endl;
std::cout << "** f(x) = x^2-4" << std::endl;
S.setFct(vector<double>{-4,0,1});
tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << ", |f(x)-0| = " << fabs(S.eval(tmp)-0) << std::endl;
tmp = S.solve(1);
std::cout << "f(x)=1: x = " << tmp << ", |f(x)-1| = " << fabs(S.eval(tmp)-1) << std::endl;
tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << std::endl;
return 0;
}
|
** f(x) = x^3+0.5 running Newton algorithm...finished after 10 steps f(x)=0: x = -0.793701, |f(x)-0| = 3.73035e-14 running Newton algorithm...finished after 6 steps f(x)=1: x = 0.793701, |f(x)-1| = 0 f(x)=0: x = -0.793701 ** f(x) = x^2-4 running Newton algorithm...finished after 6 steps f(x)=0: x = 2, |f(x)-0| = 8.88178e-15 running Newton algorithm...finished after 6 steps f(x)=1: x = 2.23607, |f(x)-1| = 8.42881e-13 f(x)=0: x = 2
lambda-Expressions und std::function¶
- In C++ gibt es eine Template Klasse die Funktionspointer ersetzt
#include <functional>einbindenstd::function<rettype(type1, type2, ...)> fctdeklariert eine Variablefctdie Funktionen mit der Signaturrettype function_name(type1 var1, type2 var2, ...)speichern kann
1 2 3 | #include <iostream>
#include <functional>
using namespace std::placeholders;
|
1 2 3 | double add(double a, double b){
return a+b;
}
|
1 2 3 | double mult(double a, double b){
return a*b;
}
|
1 2 3 4 5 6 7 8 9 | int main(){
std::function<double(double,double)> fct = add;
std::function<double(double)> multby3 = std::bind(mult,_1,3);
std::cout << "3+4 = " << fct(3,4) <<std::endl;
fct = mult;
std::cout << "3*4 = " << fct(3,4) << " = " << multby3(4) << std::endl;
return 0;
}
|
3+4 = 7 3*4 = 12 = 12
std::bind und std::function¶
- Funktionen können so kopiert, gespeichert, und sogar verändert werden
std::binderlaubt es bestimmte Input-Parameter vorzugeben- mit
std::placeholder::_1,std::placeholder::_2, ... können andere Input-Parameter noch frei gelassen werdenusing namespace std::placeholders;verkürzt die Syntax deutlich
1 2 3 | #include <iostream>
#include <functional>
using namespace std::placeholders;
|
1 2 3 | double add(double a, double b){
return a+b;
}
|
1 2 3 | double mult(double a, double b){
return a*b;
}
|
- In Zeile 3 unten wird die Addierfunktion in
fctgespeichert. Nun können wir äquivalentfctoderaddaufrufen - In Zeile 4 unten wird die Funktion
multby3definiert indem mitstd::binddas zweite Argument vonmultmit3fixiert wird und das erste Argument mit_1freigelassen wird
1 2 3 4 5 6 7 8 9 | int main(){
std::function<double(double,double)> fct = add;
std::function<double(double)> multby3 = std::bind(mult,_1,3);
std::cout << "3+4 = " << fct(3,4) <<std::endl;
fct = mult;
std::cout << "3*4 = " << fct(3,4) << " = " << multby3(4) << std::endl;
return 0;
}
|
3+4 = 7 3*4 = 12 = 12
Kurzschreibweise für Funktionen¶
- Funktionen die man nur einmal braucht (z.B. um Sie in
std::functionzu speichern), müssen nicht extra deklariert werden. - Stattdessen kann man sogenannte
lambda-Expressions verwenden
1 2 3 | [outside variable list](type1 var1, type2 var2,...)->rettype {
...
}
|
- Eine
lambda-Expression ist wie eine Funktion, die Input-Parametervar1,var2, ... übernimmt undrettypezurückgibt. - Zusätzlich können andere Variablen die bei Definition der
lambda-Expression im Scope sind im Funktionsrumpf verwendet werden, falls Sie in[outside variable list]aufgelistet werden (sogennante captured Variablen)- Standardmäsig werden diese Variablen in gleichnamige locale Variablen kopiert (Capture-By-Value)
- Wenn man ein
&vor den Variablennamen stellt wird nur eine Referenz erstellt (Capture-By-Reference)
- Es können nur lokale Variablen gecaptured werden, aber z.B. keine Membervariablen einer Klasse
- Wichtig wenn man
lambda-Expressions in einer Methode definiert - Man kann aber den
this-Pointer capturen um auf Membervariablen zuzugreifen (siehe weiter unten)
- Wichtig wenn man
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | #include <iostream>
#include <functional>
int main(){
double x=10;
std::function<void(double,double)> fct = [x](double x1, double x2)->void{ std::cout << x1+x2+x << std::endl;};
fct(3,4);
fct = [&x](double x1, double x2)->void{
std::cout << x1+x2+x << std::endl;
x=0;
};
fct(3,4);
std::cout << x << std::endl;
}
|
17 17 0
Andwendung: Funktionskomposition¶
- Sei $f\colon B\to C$ und $g\colon A\to B$ gegeben, dann ist $f\circ g\colon A\to C$ definiert als $f\circ g(x) :=f(g(x))$ für alle $x\in A$.
- mächtiges Werkzeug aus der Mathematik
- Mittels Templates und
std::functionauch sehr einfach in C++ möglich
1 2 | #include <iostream>
#include <functional>
|
1 2 3 | double roundup(double a){
return ((int)a)+1;
}
|
1 2 3 | double times2(double a){
return a*2;
}
|
- Wir schreiben schreiben ein Funktionstemplate, dass von den Definitionsbereichen und Bildbereichen
A,B, undCder Funktionen $f$ und $g$ abhängt Die Funktion
composebekommt zweistd::functionObjekte als Input und gibt die Komposition der beiden wieder alsstd::functionObjekt zurück.- Beachte: beide Inputs
fundghaben passende Input- und Returntypen - auch der Returntyp von
compsepasst zu $f\circ g$
- Beachte: beide Inputs
In Zeile 3 unten deklarieren wir die Komposition als
lambda-Expression- $f\circ g$ bekommt Datentyp
Aals Input und gibt DatentypCzurück - Wir wollen die äußeren Variablen
fundgin der Expression verwenden, daher capturen wirfundgmit[f,g]
- $f\circ g$ bekommt Datentyp
1 2 3 4 | template<typename A, typename B, typename C>
std::function<C(A)> compose(std::function<C(B)> f, std::function<B(A)> g){
return [f,g](A x)->C{return f(g(x));};
}
|
1 2 3 4 5 6 7 8 9 10 | int main(){
std::function<int(double)> ru = roundup;
std::function<double(double)> t2 = times2;
std::function<int(double)> times2roundup = compose(ru,t2);
//Alternativ auch ohne Zwischenspeichern mit Typecast möglich
/*std::function<double(double)> times2plus3 = compose((std::function<int(double)>)roundup,
(std::function<double(double)>)times2);*/
std::cout << "ceil(1.2*2) = " << times2roundup(1.2) << std::endl;
return 0;
}
|
ceil(1.2*2) = 3
Besonders elegant: Den *-Operator überladen¶
- erlaubt Schreibweise die sehr nahe an der Mathematik ist
1 2 3 4 | template<typename A, typename B, typename C>
std::function<C(B)> operator*(std::function<C(A)> f, std::function<C(B)> g){
return [f,g](B x)->A{return f(g(x));};
}
|
1 2 3 4 5 6 | int main(){
std::function<double(double)> p3 = roundup;
std::function<double(double)> t2 = times2;
std::cout << "2*ceil(1.2*2) = " << (t2*p3*t2)(1.2) << std::endl;
return 0;
}
|
2*ceil(1.2*2) = 6
Iteratoren¶
Ein Iterator ist per Definition ein Objekt, welches auf ein Element in einem Container (z.B. Vektor, Array) zeigen kann, und die Fähigkeit besitzt nacheinander auf jedes einzelen Element des Containers zu zeigen
Einfachstes Beispiel: Pointer mit Inkrement
++und Dereferenzieren*
1 2 3 4 5 6 7 8 9 10 | #include <iostream>
int main(){
double x[4] = {1,2,3,4};
double* ptr = x;
for(int i = 0; i< 4; ++i){
std::cout << *ptr << " ";
ptr++;
}
return 0;
}
|
1 2 3 4
- Iteratoren sind sehr mächtig und komplex. Wir beschränken uns auf sehr einfache Anwendungen
std::vectorhat stellt folgende Iteratoren bereitbegin: zeigt auf den ersten Eintragend: zeigt auf den (nicht existierenden) Eintrag nach dem letzten Eintragrbegin: zeigt auf den ersten Eintrag, läuft rückwärtsrend: zeigt auf den (nicht existierenden) Eintrag nach dem letzten Eintrag, läuft rückwärts
- Alle Iteratoren gibt es auch in einer konstanten Version:
cbegin,cend,crbegin,crend- Konstante Iteratoren zeigen auf konstante Daten, d.h., die Element des Vektors können gelesen aber nicht verändert werden
- Datentyp von Iteratoren ist
std::vector<type>::iteratoroderstd::vector<type>::const_iterator- kürzer: einfach
autoverwenden
- kürzer: einfach
- Wie bei Pointern kann man bei sogennanten random-access Iteratoren auch auf weiter entfernte Element zugreifen:
x.begin()[3]liefert z.B. das vierte Element des Vektors (analog auch*(x.begin()+3)- Achtung: Nicht alle Container stellen solche random-access Iteratoren zur Verfügung. Der Container
std::setzum Beispiel hat nur bidirectional Iteratoren. Diese verstehen nur Inkrement++und Dekrement--
- Achtung: Nicht alle Container stellen solche random-access Iteratoren zur Verfügung. Der Container
Einfaches Beispiel zu Iteratoren¶
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | #include <iostream>
#include <vector>
int main(){
std::vector<int> x{1,2,3,4,5};
std::vector<int>::iterator it = x.begin();
auto rit = x.rbegin();
for(int i=0; i<5;++i){
std::cout << "(" << *it << "," << *rit << ") ";
it++;
rit++;
}
std::cout << std::endl;
for(auto it = x.begin(); it < x.end();++it){
*it = 5; //Non-const iterator kann be used to modify vector entries
}
for(auto it = x.crbegin(); it < x.crend();++it){
std::cout << *it << " "; //const iterator can only be used to read vector entries
}
std::cout << std::endl;
std::cout << "Iteratorarithmetik: " << x.begin()[3] << " = " << *(x.begin()+3) << std::endl;
}
|
(1,5) (2,4) (3,3) (4,2) (5,1) 5 5 5 5 5 Iteratorarithmetik: 5 = 5
Iteratoren und neue Funktionalität von std::vector¶
- Die Methode
insertfügt ein oder mehrere Elemente an durch Iteratoren gegebener Stelle ein und verlängert dadurch den Vektorvecvec.insert(Iterator pos, type val)fügtvalvorposeinvec.insert(Iterator pos, int n, type val)fügtvalgenaun-mal vorposeinvec.insert(Iterator pos, Iterator input_start, Iterator input_end)fügt die Werte voninput_starbisinput_endvorposein
poskann auchend()sein, also auf das Element nach dem Letzten zeigen- Achtung:
inserthat Komplexität $\mathcal{O}(n)$ für Vektoren der Länge $n$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | #include <iostream>
#include <vector>
int main(){
std::vector<int> x={1,2,3,4,5};
std::vector<int> y={10};
x.insert(x.begin(),0);
for(int val : x){
std::cout << val << " ";
}
std::cout << std::endl;
y.insert(y.end(),3,0);
for(int val : y){
std::cout << val << " ";
}
std::cout << std::endl;
x.insert(x.begin()+3,y.begin(),y.end());
for(int val : x){
std::cout << val << " ";
}
std::cout << std::endl;
return 0;
}
|
0 1 2 3 4 5 10 0 0 0 0 1 2 10 0 0 0 3 4 5
Beispiel mit std::set¶
- der
setContainer enhält nur verschiedene Elemente in sortierter Reihenfolge - Elemente können hinzugefügt und entfernt werden (aber nicht verändert) (logarithmische Komplexität $\mathcal{O}(\log(n))$ statt linearer Komplexität für
std::vector) - Der Zugriffsoperator
[]ist fürsetnicht definiert. Daher braucht man für gewisse Operationen Iteratoren - Selber Code funktioniert für alle Container
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 | #include <iostream>
#include <set>
#include <vector>
int main(){
std::set<int> x = {1,2,4,5};
std::vector<int> y = {1,2,4,5};
x.insert(3);
y.insert(y.begin()+2,3);
for(int val : x){
std::cout << val << " ";
}
std::cout << std::endl;
for(auto it = x.rbegin();it != x.rend();++it){
std::cout << *it << " ";
}
std::cout << std::endl;
for(auto it = y.rbegin();it != y.rend();++it){
std::cout << *it << " ";
}
// Ohne Iteratoren nicht möglich, das []-Operator für set nicht definiert
/*
for(int i=4;i>=0;--i){
std::cout << x[i] << " ";
}*/
return 0;
}
|
1 2 3 4 5 5 4 3 2 1 5 4 3 2 1
Weitere nützliche Eigenschaften von std::set¶
- Man kann eigene Vergleichsfunktion definieren
- Vergleichsfunktion hat die Signatur
bool compare(const type& a, const type& b)und lieferttruewennakleiner alsbist, sonstfalse(Achtung:a<b == falsebedeuted nicht automatischb<=a == true, kann auch Halbordnung sein) - Muss nicht unbedingt Read-only Referenzen als Input haben, darf aber Input nicht verändern
- Vergleichfunktion kann auch
lambda-Expression sein - Zwei Elemente werden als gleich angesehen, falls weder $a<b$ oder $b<a$ gilt
1 2 3 4 | #include <iostream>
#include <set>
#include <functional>
using namespace std;
|
- Wir übergeben die Vergleichsfunktion an den Konstruktor von
std::set(Zeile 5 unten) - Wir müssen den Typ der Vergleichsfunktion angeben (Zeile 5 unten)
function<bool(double,double)>
- Die Vergleichsfunktion
compareunterscheidet nur Elemente welche mindestens 0.5 von einander entfernt sind (Zeile 3 unten) - Daher enthält
xnur Elemente welche Abstand 0.5 haben
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | int main(){
function<bool(double,double)> compare = [](double a, double b)->bool{
return a+0.5<b;
};
set<double, function<bool(double,double)> > x(compare);
x.insert(1.3);
x.insert(1.1);
x.insert(1.6);
x.insert(2.8);
cout << "x = (";
for(double val : x){
cout << val << " ";
}
cout << ")" << endl;
return 0;
}
|
x = (1.3 2.8 )
Sortieren mit std::sort¶
- Sortieralgorithmen sollte man niemals selbst schreiben sondern wenn möglich vorimplementierte Varianten verwenden
std::sortsortiert Vektor der Länge $n$ der durch Iteratoren gegeben ist in $\mathcal{O}(n\log(n))$ Schritten- Man kann eine eigene Vergleichsfunktion übergeben
- Reihenfolge gleicher Elemente bleibt nicht notwendigerweise erhalten
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | #include <iostream>
#include <vector>
int main(){
std::vector<int> x={5,3,6,1,4,7,2};
for(int val : x){
std::cout << val << " ";
}
std::cout << std::endl;
std::sort(x.begin(),x.end());
for(int val : x){
std::cout << val << " ";
}
std::cout << std::endl;
return 0;
}
|
5 3 6 1 4 7 2 1 2 3 4 5 6 7
std::sort mit eigener Vergleichsfunktion¶
- Vergleichsfunktion hat die Signatur
bool compare(const type& a, const type& b)und lieferttruewennakleiner alsbist, sonstfalse - Muss nicht unbedingt Read-only Referenzen als Input haben, darf aber Input nicht verändern
- Vergleichfunktion kann auch
lambda-Expression sein (Zeile 18-22 unten)
1 2 3 4 5 6 | #include <iostream>
#include <vector>
//Sort by last digit
bool compare(const int& a,const int& b){
return (a%10)<(b%10);
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | int main(){
std::vector<int> x={13,12,9,134,66,71};
std::cout << "x = ";
for(int val : x){
std::cout << val << " ";
}
std::cout << std::endl;
//sort by last digit
std::cout << "Sort by last digit:" << std::endl;
std::sort(x.begin(),x.end(),compare);
for(int val : x){
std::cout << val << " ";
}
std::cout << std::endl;
//sort by even < odd
std::cout << "Sort even before odd numbers:" << std::endl;
std::sort(x.begin(),x.end(),
[](const int&a, const int&b)->bool{
return (a%2)<(b%2);
}
);
for(int val : x){
std::cout << val << " ";
}
std::cout << std::endl;
return 0;
}
|
x = 13 12 9 134 66 71 Sort by last digit: 71 12 13 134 66 9 Sort even before odd numbers: 12 134 66 71 13 9
Funktion auf Vektor anwenden mit std::transform¶
#include<algorithm>einbinden- Selbe Funktion auf gesamten Vektor anwenden ohne eine
for-Schleife zu schreiben - Syntax:
std::transform(Iterator source_start, Iterator source_end, Iterator target_start, function)sourceist der Definitionsbereich auf den die Funktion angewendet werden solltargetist das Ziel in welches das Ergebnis gespeichert werden soll *sourceundtargetdürfen gleich sein (überschreiben)
1 2 3 4 5 6 | #include <iostream>
#include <vector>
#include <algorithm>
int mod2(int a){
return a%2;
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | int main(){
std::vector<int> x={13,12,9,134,66,71};
std::vector<int> y(6);
std::cout << "x = ";
for(int val : x){
std::cout << val << " ";
}
std::cout << std::endl;
std::transform(x.begin(),x.end(),y.begin(),mod2);
for(int val : y){
std::cout << val << " ";
}
std::cout << std::endl;
std::transform(x.begin()+2,x.end(),x.begin()+2,[](int a)->int{return a%2;});
for(int val : x){
std::cout << val << " ";
}
std::cout << std::endl;
return 0;
}
|
x = 13 12 9 134 66 71 1 0 1 0 0 1 13 12 1 0 0 1
algorithms Bibliothek¶
- enthält außer
std::transformnoch ganz viele andere nützliche Funktionen die ähnlich zu verwenden sind count,countifzählen Elemente in Vektorenfind,searchsuchen Elemente in Vektorenuniqueentfernt doppelte Elemente- ...
Solver Klasse mit std::function, std::set und lambda - Expressions¶
- In
SolverundSolver_Diffverwenden wirstd::functionanstelle von Funktionspointern- Vorteil: Weniger Fehleranfällig, kann mit
lambda-Expressions verwendet werden
- Vorteil: Weniger Fehleranfällig, kann mit
- In
Solververwenden wirstd::setfürsolutionsanstelle vonstd::vector- Vorteil: Wir wollen jedes Paar $(x,y)$ nur einmal im Vektor haben
- Hinzufügen und Suchen hat nur logarithmischen Aufwand (im Gegensatz zu linearem Aufwand für
std::vector)
1 2 3 4 5 | #include <iostream>
#include <set>
#include <vector>
#include <functional>
#include <cmath>
|
- Zeile 6 unten: neuer Datentyp für
fct - Zeile 11 unten:
std::setspeichert Elemente vom Typstd::vector<double>(die Paare $(x,y)$ von Lösung $x$ und rechter Seite $y$). Die Vergleichsfunction hat daher die Signaturbool compare(std::vector<double>, std::vector<double>)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | using std::vector;
using std::set;
using std::function;
class Solver {
private:
function<double(double)> fct;
protected:
double a;
double b;
double tol;
set<vector<double>, function< bool(vector<double>,vector<double>) > > solutions;
double bisection(double a, double b, double rhs, bool& error);
double lookup(double rhs, bool& notfound);
void addSol(double sol, double rhs);
public:
Solver(function<double(double)>, double a = 0, double b = 0, double tol = 1e-13);
void setDomain(double a, double b);
void setTol(double tol);
void setFct(function<double(double)> fct);
virtual double eval(double x);
double solve(double rhs);
};
|
1 2 3 4 5 6 7 8 9 10 11 12 13 | void Solver::setDomain(double a, double b){
try{
if(a>b){
throw a;
}
this->a=a;
this->b=b;
}
catch(double x){
std::cout << "Domain boundary invalid" << std::endl;
std::abort();
}
}
|
1 2 3 4 | void Solver::setFct(std::function<double(double)> fct) {
this->fct = fct;
solutions.clear();
}
|
1 2 3 | void Solver::setTol(double tol){
this->tol = tol;
}
|
- Im Konstruktor müssen wir die Vergleichsfunktion für
std::setbereitstellen- Wir machen das mit einer
lambda-Expression, welche überprüft ob $y_1+{\rm tol}<y_2$ ist (also ob sich die rechten Seiten um mehr alstolunterscheiden). - Man könnte die
lambda-Expression auch direkt in die Signatur des Konstruktors schreiben
- Wir machen das mit einer
1 2 3 4 5 6 7 8 9 10 11 12 13 | Solver::Solver(std::function<double(double)> fct, double a, double b, double tol) :
fct(fct),
a(a),
b(b),
tol(tol),
solutions(
[this](std::vector<double> a, std::vector<double> b)->bool{
if(a[1]+this->tol< b[1]){
return true;
}
return false;
}
) {}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 | double Solver::eval(double x){
try{
if(x>b || x<a){
throw x;
}
return fct(x);
}
catch(double x){
std::cout << "Evaluation point outside of domain" << std::endl;
std::abort();
}
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | double Solver::bisection(double a, double b, double rhs, bool& error){
std::cout << "running bisection algorithm...";
int counter = 0;
double m = 0, fm=0;
double fa = eval(a)-rhs;
if(fa*(eval(b)-rhs)>0){
error = true;
return 0;
}
while(b-a>2*tol){
counter++;
m = (a+b)/2;
fm = eval(m)-rhs;
if(fa*fm<=0){
b=m;
}else{
a=m;
fa=fm;
}
}
std::cout << "finished after " << counter << " steps" << std::endl;
error = false;
return m;
}
|
- Eine neue Lösung zu speichern ist nun viel einfacher
std::setüberprüft automatisch ob die Lösung (bis auf Toleranz) schon vorhanden ist (wegen eigener Vergleichsfunktion die oben programmiert wurde)
1 2 3 | void Solver::addSol(double sol, double rhs){
solutions.insert({sol,rhs});
}
|
- Die Methode
findsucht einen Eintrag insolutionsin $\mathcal{O}(\log(n))$ Schritten (sehr effizient)- Gibt eine Iterator zurück der auf die Stelle in
solutionszeigt an welcher der Eintrag gefunden wurde - Falls der gesuchte Eintrag nicht existiert zeigt der Iterator auf das erste Element nach dem letzten Eintrag (gegeben durch
end())
- Gibt eine Iterator zurück der auf die Stelle in
1 2 3 4 5 6 7 8 9 | double Solver::lookup(double rhs, bool& notfound){
auto pos = solutions.find({0,rhs});
if(pos==solutions.end()){
notfound = true;
return 0;
}
notfound = false;
return (*pos)[0];
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | double Solver::solve(double rhs){
bool error;
double tmp = lookup(rhs,error);
try{
if(error){
tmp = bisection(a,b,rhs,error);
if(error){
throw rhs;
}
addSol(tmp,rhs);
}
return tmp;
}
catch(double rhs){
std::cout << "Can't find solution for given rhs = " << rhs << std::endl;
std::abort();
}
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 | using std::function;
class Solver_Diff : public Solver {
private:
function<double(double)> deriv;
protected:
double newton(double rhs, double x, bool& error);
public:
Solver_Diff(function<double(double)>, function<double(double)>, double a = 0,
double b = 0, double tol = 1e-13);
void setDeriv(function<double(double)> deriv);
double evalDeriv(double x);
double solve(double rhs);
};
|
1 2 3 4 | void Solver_Diff::setDeriv(std::function<double(double)> deriv) {
this->deriv = deriv;
solutions.clear();
}
|
1 2 | Solver_Diff::Solver_Diff(std::function<double(double)> fct, std::function<double(double)> deriv, double a, double b, double tol) :
Solver(fct, a, b, tol), deriv(deriv) {}
|
1 2 3 4 5 6 7 8 9 10 11 12 | double Solver_Diff::evalDeriv(double x){
try{
if(x>b || x<a){
throw x;
}
return deriv(x);
}
catch(double x){
std::cout << "Evaluation point outside of domain" << std::endl;
std::abort();
}
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | double Solver_Diff::newton(double rhs, double x0, bool& error){
std::cout << "running Newton algorithm...";
double fx0,dfx0,x;
int counter = 0;
while(1){
counter++;
fx0 = eval(x0)-rhs;
if(fabs(fx0)<tol){
std::cout << "finished after " << counter << " steps" << std::endl;
error =false;
return x0;
}
dfx0 = evalDeriv(x0);
x = x0 - fx0/dfx0;
if(fabs(dfx0)<tol*fabs(fx0) || fabs(x-x0)<tol*fabs(fx0) || x<a || x>b){
std::cout << "failed! " << std::endl;
error = true;
return 0;
}
x0=x;
}
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | double Solver_Diff::solve(double rhs){
bool error;
double tmp = lookup(rhs,error);
try{
if(error){
tmp = newton(rhs,0.5*(a+b),error);
if(error){
tmp = bisection(a,b,rhs,error);
if(error){
throw rhs;
}
}
addSol(tmp,rhs);
}
return tmp;
}
catch(double rhs){
std::cout << "Can't find solution for given rhs = " << rhs << std::endl;
std::abort();
}
}
|
- In
Solver_Polyändern wir den Konstruktor so, dass wir einelambda-Expression für das Polynom und die Ableitung erstellen und auffctundderivzuweisen
1 2 3 4 5 6 7 8 | class Solver_Poly : public Solver_Diff {
private:
vector<double>coeff;
void setDeriv();
public:
Solver_Poly(vector<double> coeff = vector<double>(0), double a = 0, double b = 0, double tol = 1e-13);
void setFct(vector<double> coeff);
};
|
Wir implementieren die Funktion $f(x)$ (das Polynom) und die Ableitung als lambda-Expressions
- Die
lambda-Expressions capturen thenthis-Pointer um auf Membervariablen zugreifen zu können (siehe Zeilen 4, 17 unten). - Wir verwenden den Konstruktor
Solver_Diffum dielambda-Expressions direkt abzuspeichern
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | Solver_Poly::Solver_Poly(vector<double> coeff, double a, double b, double tol) :
Solver_Diff(
// Evaluation of the polynomial with Horner scheme
[this](double x) -> double {
int n = this->coeff.size();
if (n == 0) {
return 0;
}
double tmp = this->coeff[n - 1];
for (int i = n - 2; i >= 0; --i) {
tmp = tmp * x + this->coeff[i];
}
return tmp;
},
// Evaluation of the derivative of the polynomial with Horner scheme
[this](double x) -> double {
int n = this->coeff.size();
if (n <= 1) {
return 0;
}
double tmp = (n - 1) * this->coeff[n - 1];
for (int i = n - 2; i >= 1; --i) {
tmp = tmp * x + i * this->coeff[i];
}
return tmp;
},
a, b, tol),
coeff(coeff) {}
|
1 2 3 4 | void Solver_Poly::setFct(vector<double> coeff){
this->coeff = coeff;
solutions.clear();
}
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | int main(){
Solver_Poly S(vector<double>{0.5,0,0,1},-3,5,1e-12);
std::cout << "** f(x) = x^3+0.5" << std::endl;
double tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << ", |f(x)-0| = " << fabs(S.eval(tmp)-0) << std::endl;
tmp = S.solve(1);
std::cout << "f(x)=1: x = " << tmp << ", |f(x)-1| = " << fabs(S.eval(tmp)-1) << std::endl;
tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << std::endl;
std::cout << "** f(x) = x^2-4" << std::endl;
S.setFct(vector<double>{-4,0,1});
tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << ", |f(x)-0| = " << fabs(S.eval(tmp)-0) << std::endl;
tmp = S.solve(1);
std::cout << "f(x)=1: x = " << tmp << ", |f(x)-1| = " << fabs(S.eval(tmp)-1) << std::endl;
tmp = S.solve(0);
std::cout << "f(x)=0: x = " << tmp << std::endl;
return 0;
}
|
** f(x) = x^3+0.5 running Newton algorithm...finished after 10 steps f(x)=0: x = -0.793701, |f(x)-0| = 3.73035e-14 running Newton algorithm...finished after 6 steps f(x)=1: x = 0.793701, |f(x)-1| = 0 f(x)=0: x = -0.793701 ** f(x) = x^2-4 running Newton algorithm...finished after 6 steps f(x)=0: x = 2, |f(x)-0| = 8.88178e-15 running Newton algorithm...finished after 6 steps f(x)=1: x = 2.23607, |f(x)-1| = 8.42881e-13 f(x)=0: x = 2