Weitere Details zu Schleifen#
In Python gibt es noch weitere Schleifentypen und Besonderheiten.
Beliebig tief geschachtelte for-Schleifen#
Oft ist es nützlich, alle möglichen Kombinationen der Länge n aus den Möglichkeiten choices zu erzeugen. Dies kann mit geschachtelten for-Schleifen erreicht werden.
choices = ['A', 'B']
n = 3
for i in range(len(choices)):
for j in range(len(choices)):
for k in range(len(choices)):
print(choices[i] + choices[j] + choices[k], end=", ")
AAA, AAB, ABA, ABB, BAA, BAB, BBA, BBB,
Will man n beliebig machen, so muss man anders vorgehen. Eine Möglichkeit ist es, die Kombinationen schrittweise aufzubauen:
choices = ['A', 'B']
n=4
combinations = [""]
for i in range(n):
comb_tmp = combinations.copy()
combinations = []
for c in comb_tmp:
for choice in choices:
new_combination = c + choice
combinations.append(new_combination)
print(*combinations, sep=", ")
AAAA, AAAB, AABA, AABB, ABAA, ABAB, ABBA, ABBB, BAAA, BAAB, BABA, BABB, BBAA, BBAB, BBBA, BBBB
Alternativ kann man das Modul itertools verwenden, das eine Funktion product bereitstellt, die genau dies tut.
from itertools import product
combinations = product(['A', 'B'], repeat=4)
print(*combinations, sep=", ")
('A', 'A', 'A', 'A'), ('A', 'A', 'A', 'B'), ('A', 'A', 'B', 'A'), ('A', 'A', 'B', 'B'), ('A', 'B', 'A', 'A'), ('A', 'B', 'A', 'B'), ('A', 'B', 'B', 'A'), ('A', 'B', 'B', 'B'), ('B', 'A', 'A', 'A'), ('B', 'A', 'A', 'B'), ('B', 'A', 'B', 'A'), ('B', 'A', 'B', 'B'), ('B', 'B', 'A', 'A'), ('B', 'B', 'A', 'B'), ('B', 'B', 'B', 'A'), ('B', 'B', 'B', 'B')
While Schleifen#
Die Syntax einer while-Schleife in Python ist wie folgt:
while condition:
####
# Codeblock der ausgeführt wird, solange die Bedingung wahr ist
####
conditionist eine Bedingung, die entweder wahr (True) oder falsch (False) sein kann.Der Codeblock innerhalb der Schleife wird so lange ausgeführt, wie die Bedingung wahr ist (Wichtig: Einrückung durch Tab oder Leerzeichen beachten!)
Vor jedem Durchlauf wird die Bedingung überprüft und der Codeblock nur ausgeführt, wenn die Bedingung wahr ist.
“Solange etwas gilt, tue folgendes…”
Es ist wichtig, dass die Bedingung irgendwann falsch wird, sonst entsteht eine Endlosschleife.
Wenn die Bedingung von Anfang an falsch ist, wird der Codeblock kein einziges Mal ausgeführt (sog. Kopfgesteuerte Schleife).
i = 0
while i < 5:
print("Step ", i)
i += 1
Step 0
Step 1
Step 2
Step 3
Step 4
Bedingungsschleifen machen meist nur Sinn, wenn die Laufbedingung komplexer ist als ein einfacher Zähler. Ansonsten sind for-Schleifen meist die bessere Wahl.
Beispiel: Bisektionsverfahren mit Schleifen#
Ein gutes Bespiel hierfür ist das Bisektionsverfahren zur Nullstellenbestimmung, welches wir schon vom Kapitel über Rekursion kennen.
def f(x):
return x**2 + 1/(2+x)-2
def bisection(f, a, b, tol):
m = 0.5 * (a + b) # only necessary if while condition is never true
while b-a > 2*tol:
m = 0.5 * (a + b)
if f(a)*f(m) <= 0:
b = m
else:
a = m
return m
print("Root of f is approximately at x =", bisection(f, 0, 3, 0.001))
Root of f is approximately at x = 1.30224609375
Im obigen Beispiel gibt es ein paar überflüssige Funktionsaufrufe, die wir vermeiden können. Das ist besonders dann wichtig, wenn die Funktion f sehr aufwendig zu berechnen ist (Zum Beispiel, wenn f selbst aus einer aufwendigen Simulation kommt).
def bisection(f, a, b, tol):
fa = f(a) # store f(a) to avoid multiple calls
m = 0.5 * (a + b)
while b-a > 2*tol:
m = 0.5 * (a + b)
fm = f(m) # store f(m) to avoid multiple calls
if fa*fm <= 0:
b = m
else:
a = m
fa = fm
return m
print("Root of f is approximately at x =", bisection(f, 0, 3, 0.001))
Root of f is approximately at x = 1.30224609375
Beispiel: Euklidischer Algorithmus#
Gegeben: Zwei natürliche Zahlen \(a,b\in \mathbb{N}\)
Gesucht: Der größte gemeinsame Teiler (greatest common divisior) \(gcd(a,b)\) von \(a\) und \(b\).
Falls \(a=b\), so ist \(gcd(a,b)=a\).
Falls \(a<b\), vertausche \(a\) und \(b\).
Ersetze \(a\) durch \(a-b\).
Wiederhole die Schritte 1-3, bis \(a=b\).
Schritt 2 vertauscht die Zahlen. Das ist möglich, da \(gcd(a,b)=gcd(b,a)\) gilt. Schritt 3 verkleinert die größere Zahl. Das ist möglich, da \(gcd(a,b)=gcd(a-b,b)\) gilt.
Satz: Für \(a,b \in \mathbb{N}\) mit \(a\geq b\) gilt \(gcd(a,b) = gcd(a-b,b)\).
Beweis: Eine Zahl \(d\) teilt eine andere Zahl \(a\), genau dann wenn eine weitere Zahl \(k\in\mathbb{N}\) existiert, sodass \(a = k d\) gilt. Sei also \(d\) ein gemeinsamer Teiler von \(a\) und \(b\). Dann gibt es Zahlen \(k_a,k_b\in \mathbb{N}\) mit \(a = k_a d\) und \(b = k_b d\). Daher gilt auch
also ist \(d\) auch ein Teiler von \(a-b\) (und auch von \(a\) und \(b\)). Daher gilt \(d \leq gcd(a-b,b)\). Da \(d\) jeder Teiler von \(a\) und \(b\) sein kann, können wir auch \(d = gcd(a,b)\) wählen und erhalten \(gcd(a,b) \leq gcd(a-b,b)\). Die selbe Argumentation in die andere Richtung zeigt \(gcd(a-b,b) \leq gcd(a,b)\), woraus die Behauptung folgt. \(\square\)
Satz: Der euklidische Algorithmus terminiert nach endlich vielen Schritten für alle Inputs \(a,b\in \mathbb{N}\) mit \(a,b>0\).
Beweis: Nach Schritt 2 gilt immer \(a>b>0\). Daher haben wir \(\max\{a-b,b\}\leq \max\{a,b\}-1\). Das heißt, in jedem Durchlauf wird nach Schritt 3 die Zahl \(\max\{a,b\}\) um mindestens 1 verkleinert. Da \(\max\{a,b\}\) immer eine natürliche Zahl größer als 0 ist, kann dies nur endlich oft geschehen, bevor \(a=b\) gilt. \(\square\)
Illustration des euklidischen Algorithmus#
Wir berechnen \(gcd(6,14)=2\) mit dem euklidischen Algorithmus
Die grauen Linien verdeutlichen, dass die Zwischenergebnisse immer den selben größten gemeinsamen Teiler haben.
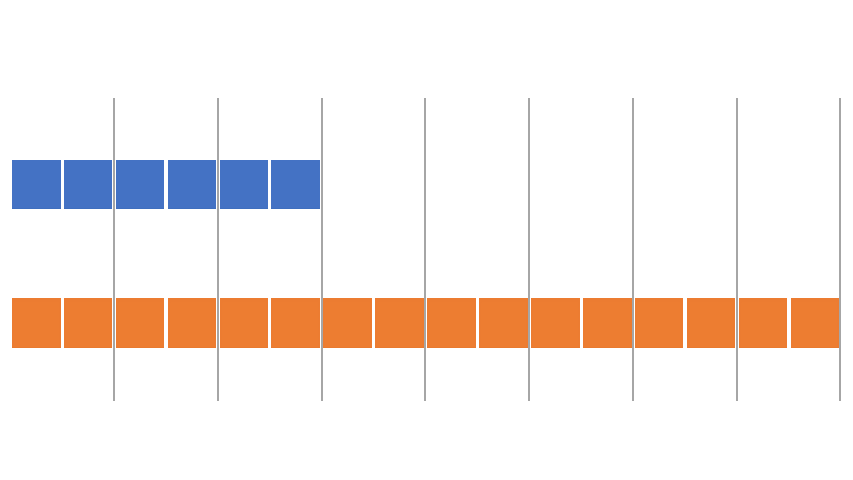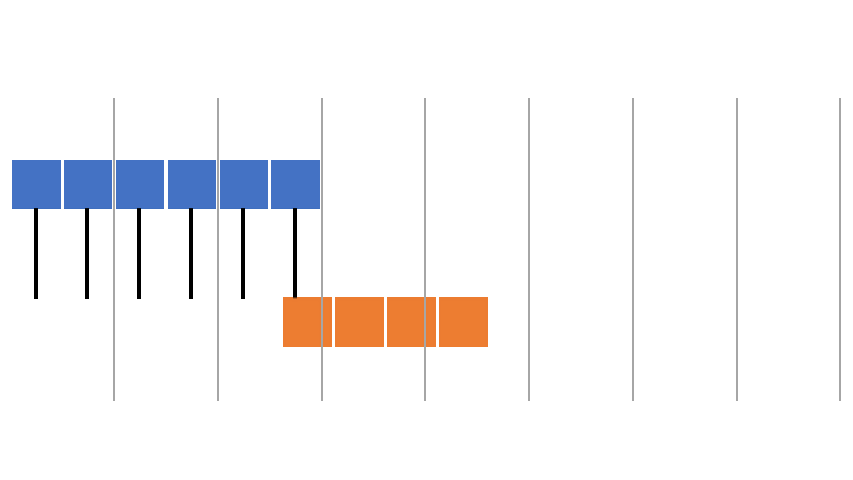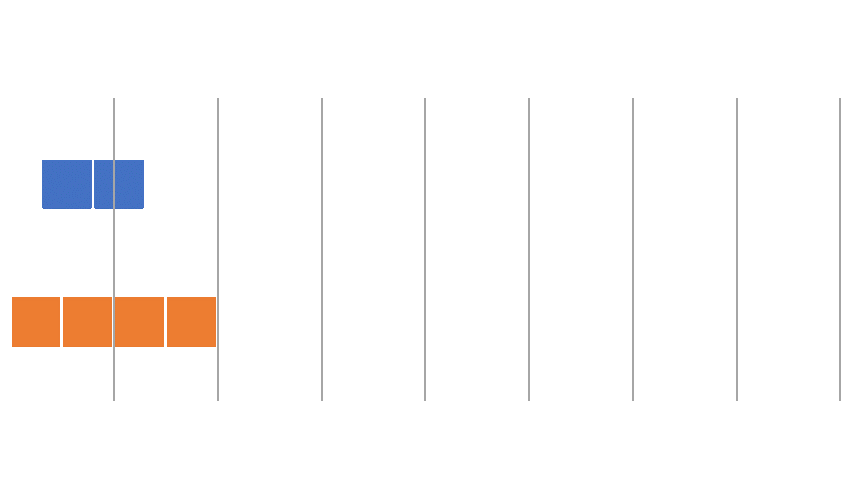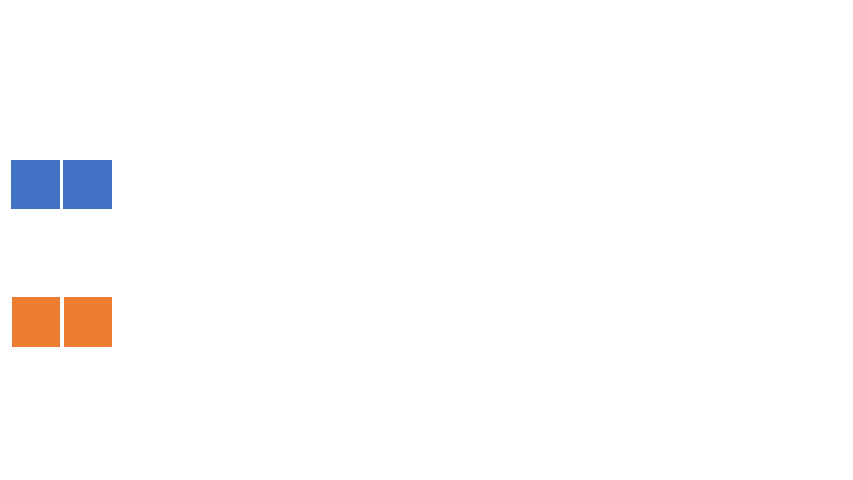
Implementierung des euklidischen Algorithmus#
berechnet \(gcd(a,b)\) für \(a,b\in \mathbb{N}\)
basiert auf \(gcd(a,b) = gcd(a-b,b)\) für \(a\geq b\)
für \(a=b\) terminiert die Schleife mit Ergebnis \(gcd(a,b)=a=b\)
def euklid(a,b):
while a != b:
if a > b:
a = a - b
else:
b = b - a
return a
print("gcd(6,14) =", euklid(6,14))
gcd(6,14) = 2
Wir können die Implementierung noch deutlich verbessern, indem wir statt \(a-b\) den Modulo-Operator % verwenden. Dieser berechnet den Rest der Division von \(a\) durch \(b\).
Euklidischer Algorithmus iteriert \(a=a-b\) solange \(a>b\) gilt.
Der Algorithmus funktioniert auch, wenn man \(a=a-b\) iteriert, solange \(a\geq b\) gilt. Der einzige Unterschied ist, dass in diesem Fall die Schleife auch dann noch einmal durchlaufen wird, wenn \(a=b\) gilt. In diesem Fall wird \(a\) durch \(a-b=0\) ersetzt und im nächsten Schritt terminiert die Schleife mit Ergebnis \(gcd(a,b)=b\).
Das ist äquivalent zu \(a = a \mod b\). Wenn \(a=0\) ist, terminiert die Schleife mit Ergebnis \(gcd(a,b)=b\).
def euklid_improved(a,b):
while a != 0:
if a < b:
a, b = b, a
a = a % b
return b
print("gcd(6,14) =", euklid_improved(6,14))
gcd(6,14) = 2
Eine weitere Beobachtung ist, dass \(a \mod b\) immer kleiner als \(b\) ist. Daher können wir die Bedingung if a < b: weglassen und immer vertauschen.
def euklid_improved_again(a,b):
while b != 0:
a, b = b, a % b
return a
print("gcd(6,14) =", euklid_improved_again(6,14))
gcd(6,14) = 2
Performance Vergleich mit time#
Diese Optimierungen sind nicht nur eine Fingerübung, sondern haben auch einen deutlichen Einfluss auf die Performance.
Wir vergleichen die Laufzeiten der drei Versionen des euklidischen Algorithmus mit dem
time-Modul.time.time()gibt die aktuelle Zeit in Sekunden seit dem 1.1.1970 zurück.
import time
a, b = 123456789, 987654321
start = time.time()
euklid(a, b)
time_euklid = time.time() - start
start = time.time()
euklid_improved(a, b)
time_euklid_improved = time.time() - start
start = time.time()
euklid_improved_again(a, b)
time_euklid_improved_again = time.time() - start
print(f"euklid: {time_euklid:.6f} seconds")
print(f"euklid_improved: {time_euklid_improved:.6f} seconds")
print(f"euklid_improved_again: {time_euklid_improved_again:.6f} seconds")
euklid: 0.429328 seconds
euklid_improved: 0.000024 seconds
euklid_improved_again: 0.000016 seconds
Auch der Unterschied zwischen Rekursion und Iteration ist deutlich messbar. Wir vergleichen dazu die rekursive und die iterative Implementierung des Bisektionsverfahrens zur Nullstellenbestimmung.
import time
def f(x):
return x**2 + 1/(2+x)-2
def bisection(f, a, b, tol):
fa = f(a) # store f(a) to avoid multiple calls
m = 0.5 * (a + b)
while b-a > 2*tol:
m = 0.5 * (a + b)
fm = f(m) # store f(m) to avoid multiple calls
if fa*fm <= 0:
b = m
else:
a = m
fa = fm
return m
def bisection_recursive(f, a, b, tol):
m = 0.5 * (a + b)
if b-a < 2*tol:
return m
if f(a)*f(m) <= 0:
return bisection_recursive(f, a, m, tol)
else:
return bisection_recursive(f, m, b, tol)
tol = 1e-15
start = time.time()
bisection(f, 0, 3000, tol)
time_bisection = time.time() - start
start = time.time()
bisection_recursive(f, 0, 3000, tol)
time_bisection_recursive = time.time() - start
print(f"bisection (iterative): {time_bisection:.6f} seconds")
print(f"bisection (recursive): {time_bisection_recursive:.6f} seconds")
bisection (iterative): 0.000036 seconds
bisection (recursive): 0.000130 seconds
Schleifenkontrolle und Else-Blöcke#
Um genauere Kontrolle über die Iterationen einer Schleife zu haben, gibt es die Befehle break und continue.
break: Beendet die Schleife sofort, unabhängig davon, ob die Schleifenbedingung noch wahr ist.continue: Überspringt den aktuellen Durchlauf der Schleife und fährt mit dem nächsten Durchlauf fort.
Vor allem break ist besonders nützlich, wenn man eine komplizierte Abbruchbedingung hat, die nicht einfach in eine Laufbedingung für die While-Schleife umgewandelt werden kann.
Beim Bisektionsverfahren kann es zum Beispiel Sinn machen, auch dann die Schleife zu beenden wenn \(f(m)\) sehr klein ist, also wenn wir eine sehr gute Näherung der Nullstelle gefunden haben.
def bisection(f, a, b, tol):
fa = f(a) # store f(a) to avoid multiple calls
m = 0.5 * (a + b)
while b-a > 2*tol:
m = 0.5 * (a + b)
fm = f(m) # store f(m) to avoid multiple calls
if abs(fm) < tol:
break # exit the loop if we found a good approximation
if fa*fm <= 0:
b = m
else:
a = m
fa = fm
return m
Um das in der Laufbedingung der While-Schleife zu realisieren, müsste man den Code wie folgt ändern (was deutlich unübersichtlicher ist):
def bisection(f, a, b, tol):
fa = f(a) # store f(a) to avoid multiple calls
m = 0.5 * (a + b)
fm = f(m)
while b-a > 2*tol and abs(fm) >= tol:
m = 0.5 * (a + b)
fm = f(m) # store f(m) to avoid multiple calls
if abs(fm) < tol:
break # exit the loop if we found a good approximation
if fa*fm <= 0:
b = m
else:
a = m
fa = fm
return m
Außerdem kann man mit break auch eine Fußgesteuerte Schleife realisieren, die mindestens einmal durchlaufen wird.
Dazu setzt man die Laufbedingung der While-Schleife auf True und bricht die Schleife mit break ab, wenn die Abbruchbedingung erfüllt ist.
Achtung: Eine solche Schleife muss immer eine break-Anweisung enthalten, sonst entsteht eine Endlosschleife!
while True:
user_input = float(input("Enter a positive number: "))
if user_input > 0:
break
print("That's not a positive number, try again.")
print("You entered:", user_input)
You entered: 3.2
Beispiel: Fibonacci-Zahlen mit Schleifen#
Erinnerung: Die Fibonacci-Zahlen sind eine Folge von Zahlen, die durch die Rekursionsvorschrift $\( F_0 = 0, \quad F_1 = 1, \quad F_n = F_{n-1} + F_{n-2} \text{ für } n\geq 2 \)$ definiert sind.
Ziel: Berechne alle Folgenglieder bis zum ersten mit \(F_n > c\) für eine gegebene Zahl \(c\in\mathbb{N}\).
Anstatt neue Variablen für jedes Folgenglied zu erstellen, ist es viel effizienter, nur zwei Variablen zu verwenden und diese in jeder Iteration zu aktualisieren.
counter = 0
F0, F1 = 0, 1
c = 10
print(F0,F1, sep=", ", end=", ")
while True:
tmp = F0 + F1
F0 = F1
F1 = tmp
print(F1, end=", ")
if F1 > c:
break
0, 1, 1, 2, 3, 5, 8, 13,
Der Befehl continue kann verwendet werden, um bestimmte Iterationen zu überspringen. In diesem Beispiel wird continue verwendet, um ungerade Fibonacci-Zahlen zu überspringen und alle geraden Fibonacci-Zahlen bis zu einer gegebenen Grenze c auszugeben.
counter = 0
F0, F1 = 0, 1
c = 10
print(F0,F1, sep=", ", end=", ")
while True:
tmp = F0 + F1
F0 = F1
F1 = tmp
if F1 % 2 == 1:
continue
print(F1, end=", ")
if F1 > c:
break
0, 1, 2, 8, 34,
else Blöcke bei Schleifen#
Genau wie bei if-Anweisungen können auch Schleifen mit einem else-Block kombiniert werden. Der Code im else-Block wird ausgeführt, wenn die Schleife regulär beendet wird, also nicht durch einen break-Befehl.
Das macht besonders bei while-Schleifen Sinn, um Code auszuführen, wenn die Schleife beendet wird, weil die Bedingung falsch ist.
while condition:
####
# Codeblock der ausgeführt wird, solange die Bedingung wahr ist
####
else:
####
# Codeblock der ausgeführt wird, wenn die Bedingung falsch ist. Die Schleife wird danach beendet.
####
Es kann aber auch bei for-Schleifen sinnvoll sein, um Code auszuführen, wenn die Schleife alle Elemente der Sequenz durchlaufen hat. Oder um Code auszuführen, wenn die sequence leer ist.
for element in sequence:
####
# Codeblock, der für jedes Element in der Sequenz ausgeführt wird
####
else:
####
# Codeblock der ausgeführt wird, wenn die Schleife regulär beendet wird (d.h. nicht durch einen `break`-Befehl)
####
vector = [1, 3, 5, 7, 9, 11, 13, 15]
target = 10
for n in vector:
if n == target:
print(f"Found {target} in vector, stopping search.")
break
else:
print(f"{target} not found in the list.")
10 not found in the list.
Sortieralgorithmen#
Sortieralgorithmen ordnen eine Liste von Elementen in einer bestimmten Reihenfolge (z.B. aufsteigend oder absteigend).
In Python gibt es die eingebaute Methode
list.sort(), aber es macht Sinn sich mit einfachen Sortieralgorithmen zu beschäftigen, um ihre Funktionsweise zu verstehen.
Bubble Sort#
Bubble Sort ist ein einfacher Sortieralgorithmus, der wiederholt benachbarte Elemente vertauscht, wenn sie in der falschen Reihenfolge sind.
Der Algorithmus wiederholt diesen Prozess, bis die Liste vollständig sortiert ist.
def bubble_sort(arr):
n = len(arr)
for i in range(n):
# Last i elements are already sorted
for j in range(0, n-i-1):
if arr[j] > arr[j+1]:
# Swap if the element found is greater than the next element
arr[j], arr[j+1] = arr[j+1], arr[j]
# Example usage
data = [64, 34, 25, 12, 22, 11, 90]
bubble_sort(data)
print("Sorted array:", data)
Sorted array: [11, 12, 22, 25, 34, 64, 90]
Minsort#
Minsort (auch Selection Sort genannt) ist ein weiterer einfacher Sortieralgorithmus, der wiederholt das kleinste (oder größte) Element aus der unsortierten Liste auswählt und es an die richtige Position in der sortierten Liste verschiebt.
def minsort(arr):
n = len(arr)
for i in range(n):
# Find the minimum element in the unsorted portion of the array
min_idx = i
for j in range(i+1, n):
if arr[j] < arr[min_idx]:
min_idx = j
# Swap the found minimum element with the first element of the unsorted portion
arr[i], arr[min_idx] = arr[min_idx], arr[i]
# Example usage
data = [64, 34, 25, 12, 22, 11, 90]
minsort(data)
print("Sorted array:", data)
Sorted array: [11, 12, 22, 25, 34, 64, 90]
Quicksort#
Quicksort ist ein effizienter Sortieralgorithmus, der das “Teile und Herrsche”-Prinzip verwendet.
Der Algorithmus wählt ein “Pivot”-Element aus der Liste und partitioniert die anderen Elemente in zwei Unterlisten: diejenigen, die kleiner als das Pivot sind, und diejenigen, die größer als das Pivot sind.
Diese Unterlisten werden dann rekursiv sortiert und zusammengeführt, um die endgültige sortierte Liste zu erhalten.
def quicksort(arr):
if len(arr) <= 1:
return arr
pivot = arr[len(arr) // 2] # Choose the middle element as the pivot
left = [x for x in arr if x < pivot] # Elements less than the pivot
middle = [x for x in arr if x == pivot] # Elements equal to the pivot
right = [x for x in arr if x > pivot] # Elements greater than the pivot
return quicksort(left) + middle + quicksort(right)
# Example usage
data = [64, 34, 25, 12, 22, 11, 90]
sorted_data = quicksort(data)
print("Sorted array using quicksort:", sorted_data)
Sorted array using quicksort: [11, 12, 22, 25, 34, 64, 90]
