Numerische Mathematik mit NumPy

Das Modul numpy (Numerical Python) stellt effiziente Datenstrukturen und Funktionen für numerische Berechnungen in Python bereit. Es ist besonders nützlich für die Arbeit mit Vektoren und Matrizen.

Installation

Falls numpy noch nicht installiert ist, kann es mit dem folgenden Befehl im VSCode Terminal installiert werden:

pip install numpy

Achtung: Wenn Sie ein venv (virtuelle Umgebung) verwenden, stellen Sie sicher, dass es aktiviert ist, bevor Sie den Installationsbefehl ausführen.

• im Terminal steht der Name des venv in Klammern, z.B. (.venv) PS C:\Pfad\zu\Ihrem\Projekt>

• Falls nicht, aktivieren Sie es mit dem Befehl:

  • Windows: .venv\Scripts\activate

  • macOS/Linux: source .venv/bin/activate

NumPy Arrays

NumPy stellt die Datenstruktur ndarray (n-dimensional array) zur Verfügung, die effizientere Speicherung und Verarbeitung von numerischen Daten ermöglicht als die Standard-Python-Listen.

array = np.array([Python-Liste], dtype = Datentyp)

Diese Funktion erstellt ein NumPy Array aus einer Python-Liste.

• Der optionale Parameter dtype gibt den Datentyp der Elemente im Array an (z.B. int, float, complex).

• Jeder Eintrag in einem NumPy Array hat den gleichen Datentyp (im Unterschied zu Python-Listen, die verschiedene Datentypen enthalten können).

• Wird dtype nicht angegeben, wird der Datentyp automatisch bestimmt.

• Verfügbare Datentypen sind

  • int (Ganzzahlen)

  • float (Gleitkommazahlen)

  • complex (komplexe Zahlen)

  • bool (Boolesche Werte)

  • str (Zeichenketten)

• Numpy-Interne Datentypen sind z.B.

  • np.float32, np.float64 (für Gleitkommazahlen mit einfacher bzw. doppelter Genauigkeit, später mehr dazu)

  • np.int32, np.int64 (für Ganzzahlen mit einfacher bzw. doppelter Genauigkeit)

  • uvm.

Wie Listen sind ndarray Objekte veränderbar (mutable), d.h. einzelne Elemente können geändert werden.

import numpy as np
a = np.array([1, 2, 3], dtype=int)
print(a)
a[0] = 10
print(a)

[1 2 3]
[10  2  3]

Zugriff auf NumPy Arrays

Der Zugriff auf Elemente in einem NumPy Array erfolgt ähnlich wie bei Python-Listen, jedoch mit einigen Erweiterungen:

• Einzelne Elemente können mit eckigen Klammern und dem Index angesprochen werden (Index beginnt bei 0).

• Mehrdimensionale Arrays können mit mehreren Indizes angesprochen werden, z.B. array[i, j] für das Element in der i-ten Zeile und j-ten Spalte.

• Slicing funktioniert ebenfalls, z.B. array[start:stop:step] für Teilarrays.

• Mehrdimensionales Slicing ist ebenfalls möglich, z.B. array[0:2, 1:3] für einen Ausschnitt eines 2D-Arrays.

• Mittels Listen kann man Teilarrays extrahieren, z.B. array[[0, 2], [1, 3]] für spezifische Elemente.

A = np.array([[1, 2, 3], [4, 5, 6]])
print(A)
print(A[0, 1])  # Zugriff auf das Element in der ersten Zeile und zweiten Spalte
print(A[0][1])  # Alternativer Zugriff
print(A[0:2, 1:3])  # Slicing
print(A[[0, 1], [1, 2]])  # Zugriff auf Teilmatrix mittels Listen
print(A[1])  # Zugriff auf die zweite Zeile gibt wieder eine NumPy Array zurück
print(A[:,2])  # Zugriff auf die dritte Spalte

[[1 2 3]
 [4 5 6]]
2
2
[[2 3]
 [5 6]]
[2 6]
[4 5 6]
[3 6]

Zugriff mittels True/False Masken:

In NumPy können Sie auch boolesche Masken verwenden, um auf bestimmte Elemente eines Arrays zuzugreifen. Eine boolesche Maske ist ein Array der gleichen Form wie das ursprüngliche Array, das True für die Elemente enthält, die Sie auswählen möchten, und False für die Elemente, die Sie ausschließen möchten.

• Nützlich, wenn Sie Elemente basierend auf einer Bedingung auswählen möchten

• Mehrdimensionale Arrays werden zeilenweise zu einem eindimensionalen Array “abgeflacht”

x = np.array([1, 2, 3, 4, 5])
mask = x > 2  # Boolesche Maske erstellen
print(mask)  # Ausgabe: [False False  True  True  True]
filtered_x = x[mask]  # Zugriff auf Elemente, die der Maske entsprechen
print(filtered_x)  # Ausgabe: [3 4 5]

A = np.array([[1, 2, 3], [4, 5, 6]])
print(A[A>2])  # Boolesche Maske erstellen

[False False  True  True  True]
[3 4 5]
[3 4 5 6]

Form und Dimensionen:

• array.shape: Gibt die Dimensionen des Arrays als Tupel zurück.

• array.ndim: Gibt die Anzahl der Dimensionen des Arrays zurück.

• array.size: Gibt die Gesamtanzahl der Elemente im Array zurück.

Ausgehend von einem Array kann man neue Arrays mit dem selben Inhalt aber anderer Form erstellen, solange die Gesamtanzahl der Elemente gleich bleibt:

• array.reshape(new_shape): Ändert die Form des Arrays.

  • new_shape ist ein Tupel, das die neuen Dimensionen angibt.

  • Eine Dimension kann als -1 angegeben werden, um sie automatisch zu berechnen (die Gesamtanzahl der Elemente muss übereinstimmen).

  • Die Umformung erfolgt durch zeilenweises Auslesen des ursprünglichen Arrays und zeilenweises Füllen des neuen Arrays.

    • Das kann mit dem Argument order beeinflusst werden:

      • order='C' (Standard): Zeilenweise (C-Stil)

      • order='F': Spaltenweise (Fortran-Stil)

• array.flatten(): Gibt eine Kopie des Arrays als eindimensionales Array zurück.

• Achtung: shape = (n,) ist ein eindimensionales Array mit n Elementen, während shape = (n, 1) ein zweidimensionales Array mit n Zeilen und 1 Spalte ist.

A = np.array([[1, 2, 3], [4, 5, 6]])
print(f"A is a {A.ndim}-dimensional array with shape {A.shape} containing {A.size} elements")
print(A)
A=A.reshape(3, 2)  # Ändert die Form des Arrays zu 3 Zeilen und 2 Spalten
print(f"A is a {A.ndim}-dimensional array with shape {A.shape} containing {A.size} elements")
print(A)
A=A.reshape(2, 3, order ='F')  # Ändert die Form des Arrays zu 2 Zeilen und 3 Spalten, Spaltenweise
print(f"A is a {A.ndim}-dimensional array with shape {A.shape} containing {A.size} elements")
print(A)
A = A.flatten()  # Macht aus einem mehrdimensionalen Array ein eindimensionales Array
print(f"A is a {A.ndim}-dimensional array with shape {A.shape} containing {A.size} elements")
print(A)

A is a 2-dimensional array with shape (2, 3) containing 6 elements
[[1 2 3]
 [4 5 6]]
A is a 2-dimensional array with shape (3, 2) containing 6 elements
[[1 2]
 [3 4]
 [5 6]]
A is a 2-dimensional array with shape (2, 3) containing 6 elements
[[1 5 4]
 [3 2 6]]
A is a 1-dimensional array with shape (6,) containing 6 elements
[1 5 4 3 2 6]

Vordefinierte Arrays:

• np.zeros(shape, dtype=float): Erstellt ein Array der angegebenen Form, gefüllt mit Nullen.

• np.zeros_like(array): Erstellt ein Array mit der gleichen Form und dem gleichen Datentyp wie das gegebene Array, gefüllt mit Nullen.

• np.ones(shape, dtype=float): Erstellt ein Array der angegebenen Form, gefüllt mit Einsen.

• np.ones_like(array): Erstellt ein Array mit der gleichen Form und dem gleichen Datentyp wie das gegebene Array, gefüllt mit Einsen.

• np.full(shape, fill_value, dtype=None): Erstellt ein Array der angegebenen Form, gefüllt mit dem angegebenen Wert.

• np.eye(n, dtype=float): Erstellt eine n x n Einheitsmatrix.

• np.arange(start, stop, step, dtype=None): Erstellt ein Array mit Werten im angegebenen Bereich (ähnlich wie die eingebaute range-Funktion, aber gibt ein NumPy Array zurück).

• np.linspace(start, stop, num, dtype=None): Erstellt ein Array mit num gleichmäßig verteilten Werten zwischen start und stop.

• np.random.rand(d0, d1, ..., dn): Erstellt ein Array mit Dimensionen d0, d1, ..., dn und füllt es mit zufälligen Werten aus einer gleichverteilten Verteilung im Bereich \([0, 1)\).

• np.random.randn(d0, d1, ..., dn): Erstellt ein Array mit Dimensionen d0, d1, ..., dn und füllt es mit zufälligen Werten aus einer Standardnormalverteilung (Mittelwert 0, Standardabweichung 1).

print(np.zeros((2,3)))  # 2x3 Array mit Nullen
print(np.ones((2,3)))   # 2x3 Array mit Einsen
print(np.full((2,3), 7))  # 2x3 Array mit dem Wert 7
print(np.eye(3))        # 3x3 Einheitsmatrix
print(np.arange(0, 10, 2))  # Array mit Werten von 0 bis 10 mit Schrittweite 2
print(np.linspace(0, 1, 5))  # Array mit 5 gleichmäßig verteilten Werten zwischen 0 und 1
print(np.random.rand(2,3))  # 2x3 Array mit zufälligen Werten aus [0, 1)
print(np.random.randn(2,3))  # 2x3 Array mit zufälligen Werten aus der Standardnormalverteilung

[[0. 0. 0.]
 [0. 0. 0.]]
[[1. 1. 1.]
 [1. 1. 1.]]
[[7 7 7]
 [7 7 7]]
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
[0 2 4 6 8]
[0.   0.25 0.5  0.75 1.  ]
[[0.74389196 0.29441823 0.1934085 ]
 [0.86677025 0.26048959 0.85568049]]
[[-0.60390814  1.0585662   0.38002227]
 [-0.05487886 -2.507997    2.23658862]]

NumPy-Arrays speichern und laden

NumPy bietet Funktionen zum Speichern und Laden von Arrays in verschiedenen Formaten:

• np.save(filename, array): Speichert ein Array im .npy-Format.

• np.load(filename): Lädt ein Array aus einer .npy-Datei.

• np.savetxt(filename, array, delimiter=','): Speichert ein Array im Textformat (z.B. CSV).

  • Der optionale Parameter delimiter gibt das Trennzeichen an (Standard ist ein Leerzeichen).

• np.loadtxt(filename, delimiter=','): Lädt ein Array aus einer Textdatei.

import numpy as np
x=np.array([1, 2, 3])
np.save("data/array1.npy", x)
y=np.load("data/array1.npy")
print(y)

[1 2 3]

3D Plots mit Matplotlib und NumPy

Matplotlib unterstützt auch 3D-Plots.

• Zuerst muss mit plt.figure() eine Figur estellt werden

• Dann wird mit add_subplot(111, projection='3d') eine 3D-Achse hinzugefügt

  • Der erste Parameter 111 bedeutet, dass die Figur 1 Zeile und 1 Spalte hat und der Subplot an Position 1 ist

• anstatt den Subplot mit subplot() zu aktivieren, müssen wir Methoden der 3D-Achse verwenden

• plot_surface() wird verwendet, um eine 3D-Oberfläche zu plotten

• cmap steuert die Farbcodierung der Oberfläche

  • es gibt viele verschiedene Colormaps, z.B. ‘viridis’, ‘plasma’, ‘inferno’, ‘magma’, ‘cividis’, etc.

• edgecolor='none' entfernt die Kantenlinien der Oberfläche für eine glattere Darstellung

• view_init(elev, azim) ändert die Perspektive der 3D-Darstellung

  • elev ist der Höhenwinkel (Elevation) in Grad

  • azim ist der Azimutwinkel (Winkel zwischen x-Achse und der Blickrichtung) in Grad

Die Daten für den Surface-Plot müssen in einem Gitter vorliegen. Dies kann mit numpy.meshgrid() erreicht werden.

• meshgrid() erstellt zwei 2D-Arrays, die die x- und y-Koordinaten eines Gitters repräsentieren

• mit Inputs X = [1,2,3] und Y = [4,5] wird z.B. folgendes Gitter erstellt:

X = [[1,2,3],
     [1,2,3]]
 Y = [[4,4,4],
     [5,5,5]]

import numpy as np
import matplotlib.pyplot as plt
X = np.linspace(-5, 5, 50)
Y = np.linspace(-5, 5, 50)
X, Y = np.meshgrid(X, Y)
Z = np.sin(np.sqrt(X**2 + Y**2))

fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
surf = ax.plot_surface(X, Y, Z, cmap='viridis', edgecolor='none')
ax.set_title('3D Surface Plot')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.view_init(30, 45) 
plt.show()

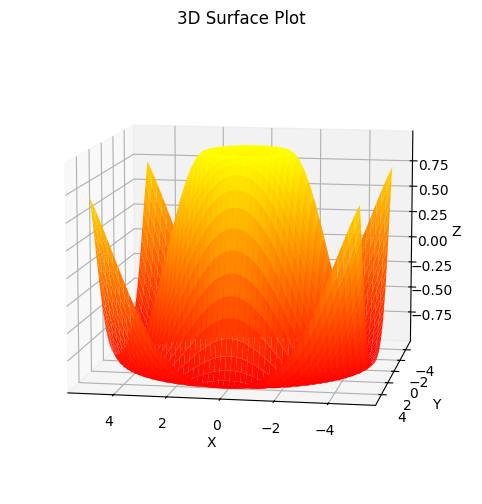
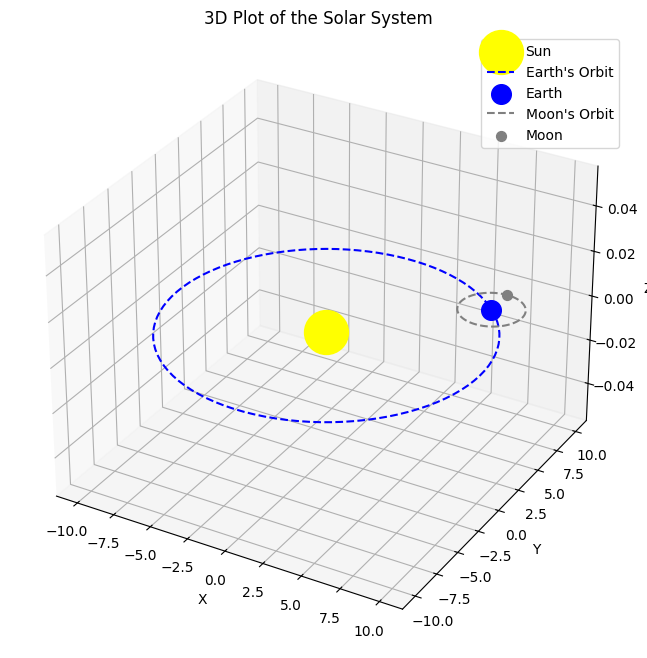
Beispiel: Plot des Sonnensystems mit Copilot

Bei komplizierteren Plots lohnt sich oft der Einsatz von KI. Auch wenn das Ergebnis nicht immer perfekt ist, kann man es oft als guten Ausgangspunkt verwenden und dann weiter anpassen. Der folgende Code wurde mit dem Prompt “Create a 3d Plot of the solar system with the sun, earth and moon” erstellt.

# Create a new figure
fig_solar = plt.figure(figsize=(8, 8))
ax_solar = fig_solar.add_subplot(111, projection='3d')

# Plot the Sun
ax_solar.scatter(0, 0, 0, color='yellow', s=1000, label='Sun')  # Sun at the origin

# Plot the Earth's orbit
earth_orbit_radius = 10
theta = np.linspace(0, 2 * np.pi, 100)
earth_orbit_x = earth_orbit_radius * np.cos(theta)
earth_orbit_y = earth_orbit_radius * np.sin(theta)
earth_orbit_z = np.zeros_like(theta)
ax_solar.plot(earth_orbit_x, earth_orbit_y, earth_orbit_z, color='blue', linestyle='--', label="Earth's Orbit")

# Plot the Earth
earth_position = (earth_orbit_radius * np.cos(np.pi / 4), earth_orbit_radius * np.sin(np.pi / 4), 0)
ax_solar.scatter(*earth_position, color='blue', s=200, label='Earth')

# Plot the Moon's orbit around the Earth
moon_orbit_radius = 2
moon_theta = np.linspace(0, 2 * np.pi, 100)
moon_orbit_x = earth_position[0] + moon_orbit_radius * np.cos(moon_theta)
moon_orbit_y = earth_position[1] + moon_orbit_radius * np.sin(moon_theta)
moon_orbit_z = np.zeros_like(moon_theta)
ax_solar.plot(moon_orbit_x, moon_orbit_y, moon_orbit_z, color='gray', linestyle='--', label="Moon's Orbit")

# Plot the Moon
moon_position = (earth_position[0] + moon_orbit_radius * np.cos(np.pi / 2),
                 earth_position[1] + moon_orbit_radius * np.sin(np.pi / 2),
                 0)
ax_solar.scatter(*moon_position, color='gray', s=50, label='Moon')

# Set labels and title
ax_solar.set_title('3D Plot of the Solar System')
ax_solar.set_xlabel('X')
ax_solar.set_ylabel('Y')
ax_solar.set_zlabel('Z')
ax_solar.legend()

plt.show()

Views (Ansichten) von NumPy Arrays

NumPy unterstützt das Konzept der “Views” (Ansichten), bei dem mehrere Variablen auf dasselbe Array im Speicher verweisen können.

• Änderungen an einer View wirken sich auf das Originalarray aus und umgekehrt.

• Der Unterschied zu normalen Variablenzuweisungen von mutable Objekten (wie Listen) ist, dass bei Views die Elemente des Arrays verschieden interpretiert werden können (z.B. andere Form oder nur ein Teil der Daten).

• Dieses Verhalten ist nützlich, um Speicherplatz zu sparen und die Leistung zu verbessern, da keine Kopien der Daten erstellt werden müssen.

Syntax:

view = array.view()

• Das direkte verwenden von view() oft nicht nötig, da viele Operationen automatisch eine View zurückgeben, z.B.

  • Slicing

  • reshape()

a = np.arange(1,1000,2)
b = a[0:10] # erzeugt einen View auf die ersten 10 Elemente von a
print(b)
b[0] = 100
print(a[0])  # a wurde auch geändert, da b ein View ist

c = a.reshape((10,50))  # erzeugt einen View auf a mit neuer Form
print(c.shape)
c[0,1] = 200
print(a[1])  # a wurde auch geändert, da c ein View ist

[ 1  3  5  7  9 11 13 15 17 19]
100
(10, 50)
200

Kopien von NumPy Arrays

• copy = array.copy(): Erstellt eine echte Kopie des Arrays im Speicher.

• Änderungen an der Kopie wirken sich nicht auf das Originalarray aus und umgekehrt.

  • nicht das selbe wie copy.copy() oder copy.deepcopy() aus dem Modul copy, da diese auch bei normalen Python-Listen verwendet werden können.

• Kopien von großen Arrays können teuer sein (allerdings erst ab tausenden oder millionen Elementen relevant).

a = np.ones((3,3))
b = a.copy()  # erzeugt eine Kopie von a
b[0,0] = 100
print(a[0,0])  # a wurde nicht geändert, da b eine Kopie ist
print(b[0,0])  # b wurde geändert

1.0
100.0

Beispiel für Views und Kopien

Folgende Illustration skizziert die Beziehung zwischen Originalarray, Shallow-Kopie, View und echter (Deep) Kopie

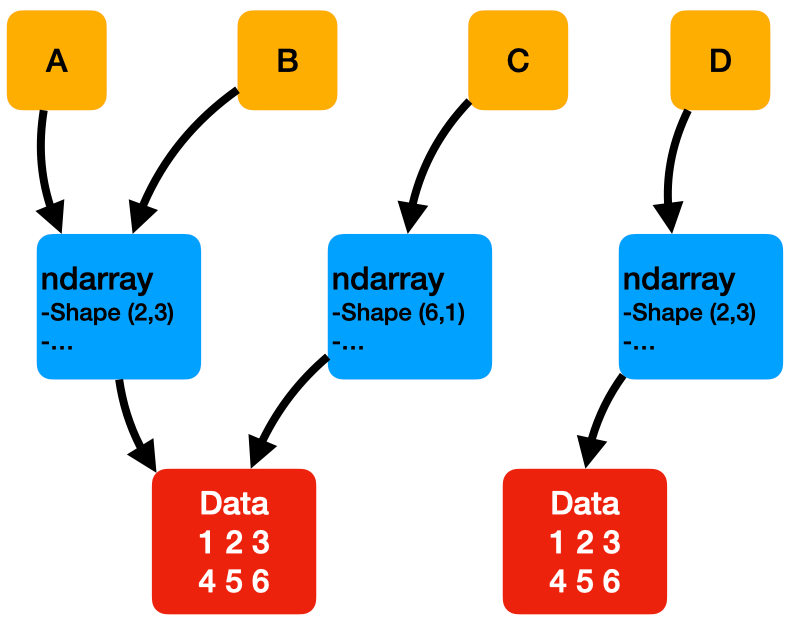
Hier ist:

• A das Original Array

• B eine Shallow-Kopie von A (z.B. durch Zuweisung B = A)

  • A und B teilen sich die Array-Struktur (Shape, Datentyp, etc.) und die Daten

• C eine View auf A (z.B. C=A.reshape(6,1))

  • A und C teilen sich die Daten, aber interpretieren diese Daten durch unterschiedliche Array-Strukturen (in diesem Fall unterschiedliche Formen)

• D eine echte Kopie von A (z.B. D=A.copy())

  • A und D sind komplett unabhängig, Änderungen an einem Array wirken sich nicht auf das andere aus

Beispiel in Code:

A = np.array([[1, 2, 3], [4, 5, 6]])
B = A
C = A.reshape(6, 1)
D = A.copy()

D[0,0] = 100
print(A) # A wurde nicht geändert, da D eine Kopie ist
C[0,0] = 200
print(A) # A wurde auch geändert, da C ein View ist
B[0,0] = 300
print(A) # A wurde auch geändert, da B nur ein anderer Name für A ist

[[1 2 3]
 [4 5 6]]
[[200   2   3]
 [  4   5   6]]
[[300   2   3]
 [  4   5   6]]

Unterscheiden zwischen Views und Kopien

Man kann überprüfen, ob ein Array eigentlich ein View ist indem man die base Eigenschaft des Arrays überprüft:

• Ist array.base None, dann ist array kein View, sondern ein Originalarray oder eine echte Kopie.

• Ist array.base nicht None, dann ist array ein View und array.base verweist auf das Originalarray, auf dem der View basiert.

A = np.array([[1, 2, 3], [4, 5, 6]])
B = A
C = A[:2,:2]
D = A.copy()
print(B.base, B is A)  # None, da B kein View ist, True, da B nur ein anderer Name für A ist
print(C)
print(C.base, C is A)  # A, da C ein View auf A ist, False, da C nicht A ist
print(D.base, D is A)  # None, da D eine Kopie ist, False, da D nicht A ist

None True
[[1 2]
 [4 5]]
[[1 2 3]
 [4 5 6]] False
None False