Klassen und Objekte#
Ein fundamentales Konzept in der objektorientierten Programmierung (OOP) sind Klassen und Objekte.
Eine Klasse ist eine Art Bauplan oder Vorlage, die beschreibt, wie ein Objekt aussehen soll und welche Eigenschaften (Attribute) und Fähigkeiten (Methoden) es haben soll.
Ein Objekt ist eine konkrete Instanz einer Klasse, die tatsächlich im Speicher existiert und verwendet werden kann.
Warum Klassen?#
Klassen helfen dabei, den Code zu strukturieren und zu organisieren, indem sie verwandte Daten und Funktionen zusammenfassen.
Sie ermöglichen die Wiederverwendung von Code, da einmal definierte Klassen mehrfach instanziiert werden können.
Klassen unterstützen Konzepte wie Vererbung (später mehr dazu), wodurch neue Klassen auf bestehenden Klassen basieren können.
Eine Klasse ist ein Datentyp, und ein Objekt ist eine Variable dieses Datentyps.
Definition einer Klasse#
Die Syntax zur Definition einer Klasse in Python ist wie folgt:
class ClassName:
### Beschreibung der Klasse
classist ein Schlüsselwort in Python, das die Definition einer Klasse einleitet.ClassNameist der Name der Klasse und jedes Wort sollte mit einem Großbuchstaben beginnen (CamelCase oder CapWords Konvention).Achtung: Einrückung und Doppelpunkt
:nicht vergessen
Die Beschreibung der Klasse beginnt meistens mit dem Konstruktor
Der Konstruktor definiert was passiert, wenn ein Objekt der Klasse erstellt wird (= eine Variable des Typs angelegt wird)
def __init__(self): # ACHTUNG: Doppelter Unterstrich vor und nach init
### Initialisierung der Attribute
self ist der Name des aktuellen Objekts der Klasse und wird automatisch an den Konstruktor übergeben.
Im folgenden Beispiel werden drei Attribute im Konstruktor definiert:
class EPROG:
def __init__(self):
self.name = "Einführung in die Programmierung"
self.lecturer = "Michael Feischl"
self.topics = ["Python", "Variablen", "Kontrollstrukturen", "Funktionen", "Klassen und Objekte"]
Um Objekte einer Klasse zu erstellen, verwendet man die Syntax:
obj = ClassName()
Mit dem Punktoperator (.) greift man auf die Attribute eines Objekts zu:
lecture = EPROG()
print(f"Modul: {lecture.name}, Dozent: {lecture.lecturer}, Themen: {lecture.topics}")
Modul: Einführung in die Programmierung, Dozent: Michael Feischl, Themen: ['Python', 'Variablen', 'Kontrollstrukturen', 'Funktionen', 'Klassen und Objekte']
Man kann die Werte der Attribute im Nachhinein ändern:
lecture1 = EPROG()
lecture2 = EPROG()
print(f"Modul: {lecture1.name}, Dozent: {lecture1.lecturer}, Themen: {lecture1.topics}")
print(f"Modul: {lecture2.name}, Dozent: {lecture2.lecturer}, Themen: {lecture2.topics}")
lecture1.lecturer = "Rando. M. Dude"
lecture1.name = "Die Kartoffel als Gemüse und Wurfgeschoss"
lecture1.topics.append("Kartoffeln")
print(f"Modul: {lecture1.name}, Dozent: {lecture1.lecturer}, Themen: {lecture1.topics}")
print(f"Modul: {lecture2.name}, Dozent: {lecture2.lecturer}, Themen: {lecture2.topics}")
Modul: Einführung in die Programmierung, Dozent: Michael Feischl, Themen: ['Python', 'Variablen', 'Kontrollstrukturen', 'Funktionen', 'Klassen und Objekte']
Modul: Einführung in die Programmierung, Dozent: Michael Feischl, Themen: ['Python', 'Variablen', 'Kontrollstrukturen', 'Funktionen', 'Klassen und Objekte']
Modul: Die Kartoffel als Gemüse und Wurfgeschoss, Dozent: Rando. M. Dude, Themen: ['Python', 'Variablen', 'Kontrollstrukturen', 'Funktionen', 'Klassen und Objekte', 'Kartoffeln']
Modul: Einführung in die Programmierung, Dozent: Michael Feischl, Themen: ['Python', 'Variablen', 'Kontrollstrukturen', 'Funktionen', 'Klassen und Objekte']
Man kann auch neue Attribute zu einem Objekt hinzufügen
Eher unüblich und sollte vermieden werden
Konvention: Alle Attribute sollten im Konstruktor definiert werden
lecture3 = EPROG()
lecture3.ects = 6 # Neues Attribut wird hinzugefügt
print(f"Modul: {lecture3.name}, Dozent: {lecture3.lecturer}, Themen: {lecture3.topics}, ECTS: {lecture3.ects}")
Modul: Einführung in die Programmierung, Dozent: Michael Feischl, Themen: ['Python', 'Variablen', 'Kontrollstrukturen', 'Funktionen', 'Klassen und Objekte'], ECTS: 6
Beispiel zu Konstruktoren#
Der Konstruktor wird automatisch aufgerufen, wenn ein Objekt der Klasse erstellt wird.
class Test:
def __init__(self):
print("Ein Objekt der Klasse Test wurde erstellt.")
t1 = Test()
t2 = Test()
Ein Objekt der Klasse Test wurde erstellt.
Ein Objekt der Klasse Test wurde erstellt.
Methoden der Klasse#
Methoden sind Funktionen, die innerhalb einer Klasse definiert sind und auf die Attribute der Klasse zugreifen können. Sie werden verwendet, um das Verhalten von Objekten zu definieren.
Da Methoden auf die Attribute des Objekts zugreifen können, haben sie immer self als ersten Parameter. Ansonsten gelten die gleichen Regeln wie bei normalen Funktionen.
def method_name(self, parameters):
### Methode, die etwas mit den Attributen macht
class EPROG:
def __init__(self):
self.name = "Einführung in die Programmierung"
self.lecturer = ["Michael Feischl"]
self.topics = ["Python", "Variablen", "Kontrollstrukturen", "Funktionen", "Klassen und Objekte"]
self.student_list = []
def add_student(self, student_name):
self.student_list.append(student_name)
def __radd__(self,student_name):
self.student_list.append(student_name)
def __add__(self,student_name):
self.student_list.append(student_name)
def list_students(self):
print("Eingeschriebene Studierende:")
for student in self.student_list:
print(f"- {student}")
lecture = EPROG()
lecture.add_student(1)
lecture.lecturer.append("Kaltenbaeck")
"Maxi" + lecture
x= EPROG()
x.add_student("Maxi")
x.add_student = "Jeromin"
print(x.lecturer)
['Michael Feischl']
Beispiel: Konstruktor mit Parametern#
Der Konstruktor kann auch weitere Parameter haben, um die Attribute eines Objekts bei der Erstellung zu initialisieren.
class Test:
def __init__(self, param1, param2):
print(f"Ein Objekt der Klasse Test mit Parametern {param1} und {param2} wurde erstellt.")
t1 = Test("Wert1", "Wert2")
t2 = Test("Wert3", "Wert4")
Ein Objekt der Klasse Test mit Parametern Wert1 und Wert2 wurde erstellt.
Ein Objekt der Klasse Test mit Parametern Wert3 und Wert4 wurde erstellt.
Ein nützlicheres Beispiel ist eine Klasse Triangle, die die Eigenschaften eines Dreiecks beschreibt:
class Triangle:
def __init__(self, a, b, c):
# Store nodes of triangle as tuples or list (x,y)
self.a = a
self.b = b
self.c = c
self.ab = ((b[0]-a[0])**2 + (b[1]-a[1])**2)**0.5
self.bc = ((c[0]-b[0])**2 + (c[1]-b[1])**2)**0.5
self.ca = ((a[0]-c[0])**2 + (a[1]-c[1])**2)**0.5
def perimeter(self):
return self.ab + self.bc + self.ca
def area(self):
# use Heron's formula Area = sqrt(s*(s-a)*(s-b)*(s-c)) with s = perimeter/2
s = self.perimeter()/2
return (s*(s-self.ab)*(s-self.bc)*(s-self.ca))**0.5
triangle = Triangle((0,0), (3,0), (0,4))
print(f"Umfang: {triangle.perimeter()}, Fläche: {triangle.area()}")
Umfang: 12.0, Fläche: 6.0
Ein weiters Beispiel ist die Klasse Polygon, die eine allgemeine Form mit einer bestimmten Anzahl von Eckpunkten beschreibt
class Polygon:
def __init__(self, vertices):
self.vertices = vertices
self.edges = []
for i in range(len(vertices)):
j = (i + 1) % len(vertices) # next vertex, wrapping around
edge_length = ((vertices[j][0] - vertices[i][0])**2 + (vertices[j][1] - vertices[i][1])**2)**0.5
self.edges.append(edge_length)
def perimeter(self):
return sum(self.edges)
def number_of_vertices(self):
return len(self.vertices)
quad = Polygon([(0,0), (4,0), (4,3), (0,3)])
print(f"Anzahl der Ecken: {quad.number_of_vertices()}, Umfang: {quad.perimeter()}")
Anzahl der Ecken: 4, Umfang: 14.0
Statische Methoden und Attribute#
Manchmal (selten) macht es Sinn Attribute oder Methoden zu definieren, die nicht an eine bestimmte Instanz der Klasse gebunden sind, sondern zur Klasse selbst gehören. Diese werden als statische Attribute und statische Methoden bezeichnet.
Statische Attribute werden außerhalb des Konstruktors definiert
Statische Attribute sollten nicht gändert werden, da sich Änderungen auf alles Objekte der Klasse auswirken
Statische Methoden werden mit dem Dekorator
@staticmethoddefiniert und haben keinenselfParameter
class ClassName:
static_attribute = value # Statisches Attribut
@staticmethod
def static_method():
# Methode, die nicht an eine Instanz gebunden ist
Statische Methoden können nützlich sein, wenn mehrere Funktionalitäten zusammengefasst werden sollen, aber kein Objekt benötigt wird.
Statische Methoden können nicht auf nicht-statische Attribute der Klasse zugreifen, da sie keinen
selfParameter haben.Statische Attribute folgen nicht den Scope-Regeln von normalen Variablen, sondern müssen immer mit dem Klassennamen referenziert werden.
Beispiel: Unten wird
Circle.piverwendet, um auf das statische Attributpizuzugreifen.
class Circle:
pi = 3.14159 # static attribute
@staticmethod
def circle_area(radius):
return Circle.pi * radius * radius
@staticmethod
def circle_perimeter(radius):
return 2 * Circle.pi * radius
def __init__(self, radius):
self.radius = radius # non-static attribute
def area(self):
return Circle.pi * self.radius**2
def perimeter(self):
return 2 * Circle.pi * self.radius
circle1 = Circle(5)
print(f"Fläche des Kreises mit Radius {circle1.radius}: {circle1.area()}")
print(f"Umfang des Kreises mit Radius {circle1.radius}: {circle1.perimeter()}")
print(f"Fläche des Kreises mit Radius 7 (statisch): {Circle.circle_area(7)}")
print(f"Umfang des Kreises mit Radius 7 (statisch): {Circle.circle_perimeter(7)}")
Fläche des Kreises mit Radius 5: 78.53975
Umfang des Kreises mit Radius 5: 31.4159
Fläche des Kreises mit Radius 7 (statisch): 153.93791
Umfang des Kreises mit Radius 7 (statisch): 43.98226
Vergisst man den Dekorator @staticmethod, wird die Methode als normale Methode interpretiert und erwartet einen self Parameter. Ein Aufruf mit Objekt führt dann zu einem Fehler.
class Circle:
pi = 3.14159 # static attribute
def circle_area(radius):
return Circle.pi * radius * radius
print(f"Fläche eines Kreises mit Radius 5: {Circle.circle_area(5)}")
circ1 = Circle()
print(f"Fläche eines Kreises mit Radius 7: {circ1.circle_area(7)}")
Fläche eines Kreises mit Radius 5: 78.53975
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[11], line 10
7 print(f"Fläche eines Kreises mit Radius 5: {Circle.circle_area(5)}")
9 circ1 = Circle()
---> 10 print(f"Fläche eines Kreises mit Radius 7: {circ1.circle_area(7)}")
TypeError: Circle.circle_area() takes 1 positional argument but 2 were given
Beispiel: Instanzen einer Klasse zählen#
Statische Attribute können verwendet werden, um z.B. die Anzahl der erstellten Instanzen einer Klasse zu zählen
class Student:
number_of_students = 0 # static attribute
def __init__(self, name):
self.name = name
self.grade = None
Student.number_of_students += 1 # increment static attribute
@staticmethod
def get_number_of_students():
return Student.number_of_students
def compute_grade(self, points):
if points >= 90:
self.grade = 'A'
elif points >= 80:
self.grade = 'B'
elif points >= 70:
self.grade = 'C'
elif points >= 60:
self.grade = 'D'
else:
self.grade = 'F'
s1 = Student("Alice")
s2 = Student("Bob")
s1.compute_grade(85)
s2.compute_grade(92)
print(f"{s1.name} hat Note {s1.grade}")
print(f"{s2.name} hat Note {s2.grade}")
print(f"Anzahl der Studierenden: {Student.get_number_of_students()}")
Alice hat Note B
Bob hat Note A
Anzahl der Studierenden: 2
Namensgleichheit von statischen und nicht-statischen Attributen#
Ein Zugriff auf self.a oder obj.a sucht zuerst nach einem nicht-statischen Attribut a der Instanz. Wenn dieses nicht existiert, wird nach einem statischen Attribut a der Klasse gesucht.
class Test:
a = 10 # Statisches Attribut der Klasse
b = 15 # Statisches Attribut der Klasse
def __init__(self):
self.a = 20 # Instanzattribut der Instanz
obj = Test()
print(f"obj.a = {obj.a}") # Greift auf das Instanzattribut zu, das statische Attribut wird verdeckt
print(f"obj.b = {obj.b}") # Greift auf das statische Attribut zu
print(f"Test.a = {Test.a}") # Greift auf das statische Attribut der Klasse zu
obj.a = 20
obj.b = 15
Test.a = 10
(Fast) Alles ist ein Objekt#
In Python ist alles ein Objekt, z.B. auch Funktionen und Klassen selbst.
Man kann neue Attribute zu Funktionen hinzufügen
Erschwert die Lesbarkeit des Codes und sollte vermieden werden
Funktionen haben vordefinierte Attribute, wie
__name__, __doc__, __closure__, __dict__, __code__, __annotations__, __defaults__und__module__.Funktionen haben auch ein self Attribut, wenn sie als Methoden in einer Klasse definiert sind.
Funktion haben auch Methoden, wie
__call__(),__get__(),…Diese Methoden werden selten direkt verwendet, sondern sind für spezielle Anwendungsfälle gedacht.
from math import sqrt
def test_function(x):
return x * x
def sqrt(x):
return 0
print(sqrt.__module__)
test_function.var = 5
test_function.my_func = lambda y: y + 10
print("test_function.my_func(3) =", test_function.my_func(3))
print("test_function.var =", test_function.var)
print("test_function.__name__ =", test_function.__name__)
print("test_function.__doc__ =", test_function.__doc__)
print("test_function.__module__ =", test_function.__module__)
__main__
test_function.my_func(3) = 13
test_function.var = 5
test_function.__name__ = test_function
test_function.__doc__ = None
test_function.__module__ = __main__
Mit einfachen Variablen funktioniert das nicht. Diese sind in Python optimiert und können daher keine neuen Attribute bekommen.
x = [1,2,4]
x.var = 5
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
Cell In[15], line 2
1 x = [1,2,4]
----> 2 x.var = 5
AttributeError: 'list' object has no attribute 'var'
Zugriffskontrolle#
Waurm ist Zugriffskontrolle wichtig?
In vielen Programmiersprachen gibt es Mechanismen, um den Zugriff auf bestimmte Attribute oder Methoden einer Klasse zu beschränken.
Dies hilft, die Integrität der Daten zu schützen und verhindert, dass externe Code Teile die internen Details einer Klasse unbeabsichtigt verändern.
Im obigen Beispiel der Student Klasse könnte man beispielsweise einfach das Attribut number_of_students von außerhalb der Klasse ändern, ohne weitere Studierende anzulegen.
s3 = Student("Charlie")
print(f"Anzahl der Studierenden: {Student.get_number_of_students()}")
Student.number_of_students = 10 # Manipulation von außen
print(f"Anzahl der Studierenden: {Student.get_number_of_students()}")
Anzahl der Studierenden: 3
Anzahl der Studierenden: 10
Wichtig: Zugriffskontrolle kann keine böswilligen Angriffe verhindern, sondern soll nur unabsichtliche Änderungen verhindern.
Dient der Fehlervermeidung: Was nicht verändert werden soll, kann auch nicht verändert werden
Führt zu besser wartbarem Code (vor allem in großen Projekten)
Zugriffskontrolle in Python#
In Python gibt es leider keine strikte Zugriffskontrolle wie in einigen anderen Programmiersprachen (z.B. private, protected, public in Java oder C++).
Alle Attribute und Methoden einer Klasse sind standardmäßig öffentlich (public) und können von außerhalb der Klasse zugegriffen werden.
Es gibt jedoch eine Konvention, um anzuzeigen, dass bestimmte Attribute oder Methoden als “privat” betrachtet werden sollten:
Ein einzelner Unterstrich (
_) signalisiert, dass das Attribut oder die Methode als “geschützt” betrachtet werden sollte und nicht direkt von außerhalb der Klasse verwendet werden sollte.Ein doppelter Unterstrich (
__) führt zu einer internen Namensänderung (Name Mangling), die den direkten Zugriff von außerhalb der Klasse erschwert.Achtung, mehr als ein Unterstrich am Ende des Names hebt den Schutz wieder auf (siehe z.bei
__init__)
class Example:
public_attr = "Ich bin öffentlich"
_protected_attr = "Ich bin geschützt"
__private_attr = "Ich bin privat"
def public_method(self):
print("Dies ist eine öffentliche Methode.")
def _protected_method(self):
print("Dies ist eine geschützte Methode.")
def __private_method(self):
print("Dies ist eine private Methode.")
ex = Example()
ex.public_method() # Funktioniert
ex._protected_method() # Funktioniert, aber sollte nicht verwendet werden
#ex.__private_method() # Führt zu einem Fehler
print(Example.__private_attr)
Dies ist eine öffentliche Methode.
Dies ist eine geschützte Methode.
---------------------------------------------------------------------------
AttributeError Traceback (most recent call last)
Cell In[17], line 18
16 ex._protected_method() # Funktioniert, aber sollte nicht verwendet werden
17 #ex.__private_method() # Führt zu einem Fehler
---> 18 print(Example.__private_attr)
AttributeError: type object 'Example' has no attribute '__private_attr'
Tatsächlich ist der Zugriff auf solche “privaten” Methoden immer noch möglich. Der doppelte Unterstrich führt lediglich zu folgener internen Umbenennung:
Eine Methode
__private_methodin der KlasseMyClasswird intern zu_MyClass__private_method
ex._Example__private_method() # Funktioniert, aber sollte nicht verwendet werden
ex._Example__private_attr = 10 # Funktioniert, aber sollte nicht verwendet werden
Dies ist eine private Methode.
Beispiel: Student Klasse mit Zugriffskontrolle#
class Student:
__number_of_students = 0 # static attribute
def __init__(self, name):
self.name = name
self.grade = None
Student.__number_of_students += 1 # increment static attribute
@staticmethod
def get_number_of_students():
return Student.__number_of_students
def compute_grade(self, points):
if points >= 90:
self.grade = 'A'
elif points >= 80:
self.grade = 'B'
elif points >= 70:
self.grade = 'C'
elif points >= 60:
self.grade = 'D'
else:
self.grade = 'F'
s1 = Student("Alice")
s2 = Student("Bob")
print(f"Anzahl der Studierenden: {Student.get_number_of_students()}")
Student.__number_of_students = 10
print(Student.get_number_of_students())
Anzahl der Studierenden: 2
2
Beispiel: Klasse für Brüche#
Verwende assert um Division durch Null zu verhindern
Kürze Brüche automatisch
class Fraction:
def __init__(self, numerator, denominator):
# Make sure that denominator is non-zero and both are integers
assert denominator != 0, "Denominator cannot be zero"
assert isinstance(numerator, int) and isinstance(denominator, int), "Numerator and Denominator must be integers"
self.__numerator = numerator
self.__denominator = denominator
self.simplify()
# Euclidean algorithm for GCD, used in simplify but can also be used independently of the Object
@staticmethod
def gcd(a, b):
while b!=0:
a, b = b, a % b
return a
# Remove common factors from numerator and denominator and make sure that denominator is positive
def simplify(self):
common_divisor = Fraction.gcd(abs(self.__numerator), abs(self.__denominator))
self.__numerator //= common_divisor
self.__denominator //= common_divisor
if self.__denominator < 0: # keep denominator positive
self.__numerator = -self.__numerator
self.__denominator = -self.__denominator
def print(self):
self.simplify() # ensure fraction is simplified before printing
if self.__denominator == 1:
print(f"{self.__numerator}") # print only numerator if denominator is 1
else:
print(f"{self.__numerator}/{self.__denominator}")
# Use of GCD without creating an object
print(f"GCD of 48 and 18 is {Fraction.gcd(48, 18)}")
# Testing the Fraction class
f1 = Fraction(4, -8)
f1.print()
f1._Fraction__numerator = 10
f1.print()
f2 = Fraction(10, 25)
f2.print()
print(f2)
f3 = Fraction(3, 0) # Löst AssertionError aus
GCD of 48 and 18 is 6
-1/2
5
2/5
<__main__.Fraction object at 0x11620f340>
---------------------------------------------------------------------------
AssertionError Traceback (most recent call last)
Cell In[20], line 46
44 f2.print()
45 print(f2)
---> 46 f3 = Fraction(3, 0) # Löst AssertionError aus
Cell In[20], line 4, in Fraction.__init__(self, numerator, denominator)
2 def __init__(self, numerator, denominator):
3 # Make sure that denominator is non-zero and both are integers
----> 4 assert denominator != 0, "Denominator cannot be zero"
5 assert isinstance(numerator, int) and isinstance(denominator, int), "Numerator and Denominator must be integers"
6 self.__numerator = numerator
AssertionError: Denominator cannot be zero
Beispiel: Klasse für die formatierte Ausgabe von Matrizen#
Die folgende Klasse soll Matrizen schön formatiert ausgeben. Dazu kann die Anzahl der gewünschten Nachkommastellen angegeben werden.
Die Klasse hat ein Attribut
matrix, das die Matrix als Liste von Listen speichert.Die Klasse hat eine Methode
print, welche die Matrix formatiert ausgibt.
class MatrixPrinter:
def __init__(self, matrix):
self.matrix = matrix
def print(self, precision=2):
# Find maximum length of matrix entries for formatting
max_len = max([len(f"{val:.{precision}f}") for row in self.matrix for val in row])
# Print each row with formatted entries
for row in self.matrix:
print("|", " ".join(f"{val:{max_len}.{precision}f}" for val in row), "|")
matrix = MatrixPrinter([[1, 12.3456, 3], [4, 500, 6.789], [7.1, 8, 9]])
print("Matrix mit Standardgenauigkeit (2 Nachkommastellen):")
matrix.print()
print("Matrix mit 0 Nachkommastellen:")
matrix.print(5)
Matrix mit Standardgenauigkeit (2 Nachkommastellen):
| 1.00 12.35 3.00 |
| 4.00 500.00 6.79 |
| 7.10 8.00 9.00 |
Matrix mit 0 Nachkommastellen:
| 1.00000 12.34560 3.00000 |
| 4.00000 500.00000 6.78900 |
| 7.10000 8.00000 9.00000 |
Die Code Zeile, welche die maximale Länge eines Eintrags in der Matrix bestimmt verdient eine genauere Erklärung:
max_len = max([len(f"{val:.{precision}f}") for row in self.matrix for val in row])
f"{val:.{precision}f}"ist ein f-String, der den Wertvalals Fließkommazahl mit der angegebenen Anzahl von Nachkommastellen (precision) formatiert.Hierbei werden die geschweiften Klammen geschachtelt, um die Variable
precisioninnerhalb des f-Strings zu verwenden.
Die Methode
lenbestimmt dann die Länge des formatierten Strings, also die Anzahl der Zeichen die benötigt werden, um die Zahl darzustellen.[... for row in self.matrix for val in row]erstellt eine Liste aller Längen der formatierten Strings, indem über alle Zeilen und Werte in der Matrix iteriert wird.Die Funktion
maxbestimmt dann die maximale Länge aus dieser Liste, also die Länge des längsten Eintrags in der Matrix.
Die Ausgabe der Matrix erfolgt dann zeilenweise, wobei jeder Eintrag rechtsbündig mit der maximalen Länge formatiert wird.
Dabei wird wieder ein f-String verwendet, wobei die Breite des Feldes durch max_len bestimmt wird
f"{val:{max_len}.{precision}f}"
Die Methode
joinverbindet die formatierten Einträge einer Zeile mit einem Leerzeichen zu einem einzigen String, der dann ausgegeben wird.
Magic Methods#
Magische Methoden (auch als “Dunder Methods” bezeichnet, da sie mit doppeltem Unterstrich beginnen und enden) sind spezielle Methoden in Python, die es ermöglichen, das Verhalten von Objekten zu definieren und anzupassen.
Magische Methoden beginnen und enden mit doppeltem Unterstrich
Beispiel:
__init__
Magische Methoden werden automatisch von Python aufgerufen, wenn bestimmte Operationen auf Objekten ausgeführt werden
Sie sind nützlich um benutzerdefinierte Klassen nahtlos in Python zu integrieren und das Verhalten von Objekten zu steuern.
Eine Liste der wichtigsten magischen Methoden ist:
Magische Methode |
Beschreibung |
|---|---|
|
Konstruktor der Klasse, wird aufgerufen, wenn ein neues Objekt erstellt wird |
|
Definiert die String-Repräsentation des Objekts, wird von |
|
Definiert die Integer-Repräsentation des Objekts, wird von |
|
Definiert die Float-Repräsentation des Objekts, wird von |
|
Definiert die Complex-Repräsentation des Objekts, wird von |
|
Definiert das Verhalten des |
|
Definiert das Verhalten des |
|
Definiert das Verhalten des |
|
Definiert das Verhalten des |
|
Definiert das Verhalten des |
|
Definiert das Verhalten des |
|
Definiert das Verhalten des |
|
Definiert das Verhalten des |
|
Definiert das Verhalten des |
|
Definiert das Verhalten des |
|
Definiert das Verhalten des |
|
Definiert das Verhalten der |
|
Definiert das Verhalten des Indexzugriffs (z.B. |
|
Definiert das Verhalten des Setzens von Werten über Indexzugriff (z.B. |
|
Definiert das Verhalten des Löschens von Werten über Indexzugriff (z.B. |
Beispiel: Arithmetik mit der Bruchklasse#
In der Klasse für Brüche kann die __str__-Methode statt der print-Methode definiert werden, um eine benutzerfreundliche String-Darstellung des Objekts zu ermöglichen.
Die anderen magischen Methoden ermöglichen es, Brüche wie normale Zahlen zu behandeln, z.B. durch Addition, Multiplikation oder Vergleich.
class Fraction:
def __init__(self, numerator, denominator):
# Make sure that denominator is non-zero and both are integers
if denominator == 0:
raise ZeroDivisionError("Denominator cannot be zero")
if not isinstance(numerator, int) or not isinstance(denominator, int):
raise TypeError("Numerator and Denominator must be integers")
self.numerator = numerator
self.denominator = denominator
self.simplify()
# Euclidean algorithm for GCD, used in simplify but can also be used independently of the Object
@staticmethod
def gcd(a, b):
while b:
a, b = b, a % b
return a
# Remove common factors from numerator and denominator and make sure that denominator is positive
def simplify(self):
common_divisor = Fraction.gcd(abs(self.numerator), abs(self.denominator))
self.numerator //= common_divisor
self.denominator //= common_divisor
if self.denominator < 0: # keep denominator positive
self.numerator = -self.numerator
self.denominator = -self.denominator
def __str__(self):
self.simplify() # ensure fraction is simplified before printing
if self.denominator == 1:
return f"{self.numerator}" # return only numerator if denominator is 1
else:
return f"{self.numerator}/{self.denominator}"
def __int__(self):
return round(self.numerator / self.denominator)
def __float__(self):
return self.numerator / self.denominator
def __add__(self, other):
if isinstance(other, Fraction):
new_numerator = self.numerator * other.denominator + other.numerator * self.denominator
new_denominator = self.denominator * other.denominator
return Fraction(new_numerator, new_denominator)
else:
raise ValueError("Both summands must be of type Fraction")
def __mul__(self, other):
if isinstance(other, Fraction):
return Fraction(self.numerator * other.numerator, self.denominator * other.denominator)
else:
raise ValueError("Can only multiply by another Fraction")
def __eq__(self, other):
if isinstance(other, Fraction):
return self.numerator * other.denominator == self.denominator * other.numerator
else:
return False
# Testing the Fraction class
f1 = Fraction(4, -8)
f2 = Fraction(10, 5)
print(f"4 divided by -8 simplifies to {f1}, while 10 divided by 5 simplifies to {f2}.")
f3 = Fraction(22,7)
print(f"{f3} rounded to the next integer is {int(f3)}, with error {float(f3) - int(f3)}.")
print(f"Summe von {f1} und {f2} ist {f1 + f2}.")
print(f"Produkt von {f1} und {f2} ist {f1 * f2}.")
print(f"Sind {f1} und {f2} gleich? {'Ja' if f1 == f2 else 'Nein'}")
4 divided by -8 simplifies to -1/2, while 10 divided by 5 simplifies to 2.
22/7 rounded to the next integer is 3, with error 0.1428571428571428.
Summe von -1/2 und 2 ist 3/2.
Produkt von -1/2 und 2 ist -1.
Sind -1/2 und 2 gleich? Nein
Beispiel: Klasse für Kreise mit Index- und Vergleichsoperatoren#
Wir erweiteren die Klasse Circle mit dem Indexoperator [] um schnell auf die Attribute radius und center zugreifen zu können.
Zusätzlich implementieren wir Vergleichsoperatoren
Wir definieren \(C_1\leq C_2\), wenn der Kreis \(C_1\) in \(C_2\) enthalten ist
D.h. der Radius von \(C_1\) plus der Abstand der Mittelpunkte ist kleiner gleich dem Radius von \(C_2\)
Wir definieren \(C_1 \geq C_2\), wenn der Kreis \(C_2\) in \(C_1\) enthalten ist
D.h. der Radius von \(C_2\) plus der Abstand der Mittelpunkte ist kleiner gleich dem Radius von \(C_1\)
Es kann sein, dass weder \(C_1 \leq C_2\) noch \(C_1 \geq C_2\) gilt!
class Circle:
pi = 3.14159 # static attribute
def __init__(self, center, radius):
self.center = center
self.radius = radius
def area(self):
return Circle.pi * self.radius * self.radius
def circumference(self):
return 2 * Circle.pi * self.radius
def __getitem__(self, index):
if index == 0:
return self.center
elif index == 1:
return self.radius
else:
raise IndexError("Index out of range. Use 0 for center and 1 for radius.")
def __setitem__(self, index, value):
if index == 0:
self.center = value
elif index == 1:
self.radius = value
else:
raise IndexError("Index out of range. Use 0 for center and 1 for radius.")
def distance_to_point(self, point):
return ((point[0] - self.center[0])**2 + (point[1] - self.center[1])**2)**0.5
def __le__(self, other):
if isinstance(other, Circle):
return self.distance_to_point(other.center) + self.radius <= other.radius
else:
raise ValueError("Can only compare with another Circle")
def __ge__(self, other):
if isinstance(other, Circle):
return self.distance_to_point(other.center) + other.radius <= self.radius
else:
raise ValueError("Can only compare with another Circle")
C1 = Circle((0,0), 5)
C2 = Circle((3,4), 2)
C3 = Circle((10,10), 3)
print(f"C1 Fläche: {C1.area()}, Umfang: {C1.circumference()}")
print(f"C1 Mittelpunkt: {C1[0]}, Radius: {C1[1]}")
C1[0] = (1,1)
C1[1] = 6
print(f"Neuer C1 Mittelpunkt: {C1[0]}, Neuer Radius: {C1[1]}")
print(f"Ist C2 in C1? {'Ja' if C1 >= C2 else 'Nein'}")
print(f"Ist C1 in C2? {'Ja' if C2 >= C1 else 'Nein'}")
print(f"Ist C3 in C1? {'Ja' if C1 >= C3 else 'Nein'}")
C1 Fläche: 78.53975, Umfang: 31.4159
C1 Mittelpunkt: (0, 0), Radius: 5
Neuer C1 Mittelpunkt: (1, 1), Neuer Radius: 6
Ist C2 in C1? Ja
Ist C1 in C2? Nein
Ist C3 in C1? Nein
# Visualisierung, siehe Kapitel "Visualisierung mit Matplotlib" zur Erklärung
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
circles = [C1, C2, C3]
colors = ['blue', 'green', 'red']
labels = ['C1', 'C2', 'C3']
for circle, color, label in zip(circles, colors, labels):
circle_patch = plt.Circle(circle.center, circle.radius, color=color, alpha=0.5, label=label)
ax.add_patch(circle_patch)
ax.plot(circle.center[0], circle.center[1], 'o', color=color) # Mark center
ax.set_xlim(-10, 15)
ax.set_ylim(-10, 15)
ax.set_aspect('equal', adjustable='datalim')
plt.legend()
plt.title("Visualisierung der Kreise")
plt.xlabel("x")
plt.ylabel("y")
plt.grid(True)
plt.show()
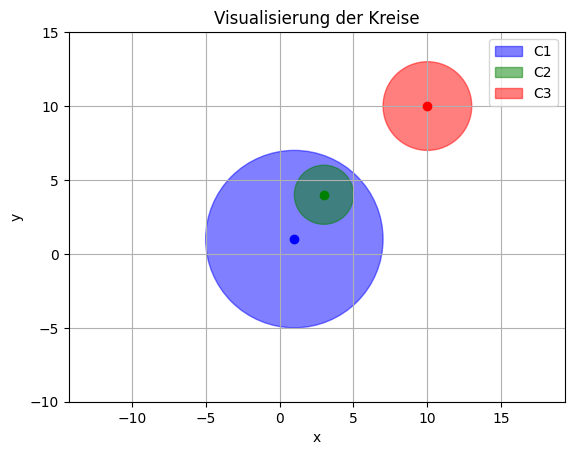
Sortieren mit Halbordnung#
Die Vergleichsoperatoren für die Klasse Circle definieren nur eine Halbordnung, da es Paare von Kreisen geben kann, die nicht vergleichbar sind (weder <= noch >= gilt).
Daher sortiert die Funktion sorted eine Liste von Kreisen, sodass alle Kreise die in andere Kreise enthalten sind, vor diesen Kreisen stehen.
from functools import cmp_to_key
def compare_containment(c1, c2):
if c1 >= c2:
return -1 # c1 contains c2, c1 should come before c2
elif c2 >= c1:
return 1 # c2 contains c1, c2 should come before c1
else:
return 0
circles_sorted = sorted(circles, key=cmp_to_key(compare_containment))
print("\nKreise sortiert nach Enthaltensein (größere zuerst):")
for c in circles_sorted:
print(f"Mittelpunkt={c.center}, Radius={c.radius}")
Kreise sortiert nach Enthaltensein (größere zuerst):
Mittelpunkt=(1, 1), Radius=6
Mittelpunkt=(3, 4), Radius=2
Mittelpunkt=(10, 10), Radius=3
