Aufwand von Algorithmen

Aufwand von Algorithmen#

Aufwand eines Algorithmus#

wichtige Kenngröße für Algorithmen
- um Algorithmen zu bewerten / vergleichen
Aufwand = Anzahl benötigter Operationen
- Zuweisungen
- Vergleiche
- arithmetische Operationen
programmspezifische Operationen nicht gezählt
- Deklarationen & Initialisierungen
- Schleifen, Verzweigungen etc.
- Zählvariablen in Schleifen
Aufwand wird durch “`einfaches”’ Zählen ermittelt
Konventionen zum Zählen nicht einheitlich
in EPROG ist Aufwand für worst case interessant
- d.h. maximaler Aufwand im schlechtesten Fall
häufig ist auch “mittlerer Aufwand” interessant (d.h. Erwartungswert des Aufwands)
- mathematisch komplizierter
- deshalb nicht in EPROG
in EPROG (maximal) benötigte Formeln:

\[ \sum_{j=1}^n 1 = n, \quad\quad \sum_{j=1}^n j = \frac{n(n+1)}{2}, \quad\quad \sum_{j=1}^n j^2 = \frac{n(n+1)(2n+1)}{6} \]

Beispiel: Maximum suchen#

Beim Zählen wird jede Schleife zu einer Summe!
- d.h. for in Zeile 3 ist \(\sum_{i=1}^{n-1}\)
- \(n\) = Länge des Arrays
Aufwand:
- 1 Zuweisung in Zeile 2
- In jedem Schritt der for-Schleife \(\rightsquigarrow\) Zeile 3-6
  - 1 Zuweisung in Zeile 4
  - 1 Vergleich in Zeile 5
  - ggf. 1 Zuweisung in Zeile 6 (im worst case immer)
insgesamt Operationen

\[ 1 + \sum_{i=1}^{n-1} 3 = 1+3(n-1)=3n-2 \]

wobei Zählvariable nicht in Aufwand eingeht, d.h. nur Statement der for-Schleife wird berücksichtigt

def mymax(arr):
    max_val = arr[0]
    for i in range(1, len(arr)):
        val = arr[i]
        if val > max_val:
            max_val = val
    return max_val

Landau-Symbol \(\mathcal{O}\) (= groß-O)#

oft nur Größenordnung des Aufwands interessant
Schreibweise \( f=\mathcal{O}(g)\) für \( x\to x_0\)
- heißt \(\displaystyle\limsup_{x\rightarrow x_0}\Bigg|\frac{f(x)}{g(x)}\Bigg|<\infty\)
- d.h. es existiert eine Konstante \(C > 0\) mit
- i \(|f(x)| \le C\,|g(x)|\) für \(x\to x_0\).
- d.h. \(f\) wächst höchstens so schnell wie \(g\) für \(x\to x_0\)
Beispiel: Maximum suchen
- Aufwand \(2n-1=\mathcal{O}(n)\) für \(n\rightarrow\infty\)<
häufig entfällt “für \( x\to x_0\)”
- dann Grenzwert \(x_0\) kanonisch z.B. \(2n-1 = \mathcal{O}(n)\)
Sprechweise (nur Beispiele):
- Algorithmus hat linearen Aufwand, falls Aufwand \(\mathcal{O}(n)\) bei Problemgröße \(n\) * Maximumssuche hat linearen Aufwand
- Algorithmus hat fastlinearen Aufwand, falls Aufwand \(\mathcal{O}(n\log n)\) bei Problemgröße \(n\)
- Algorithmus hat quadratischen Aufwand, falls Aufwand \(\mathcal{O}(n^2)\) bei Problemgröße \(n\)
- Algorithmus hat kubischen Aufwand, falls Aufwand \(\mathcal{O}(n^3)\) bei Problemgröße \(n\)
- Algorithmus hat exponentiellen Aufwand, falls Aufwand \(\mathcal{O}(2^n)\) bei Problemgröße \(n\)

Suchen im Vektor#

Aufgabe:
- Suche Index \(j\) mit vector[j] = value
- Rückgabe \(-1\), falls solcher nicht existiert
in jedem Schritt der \(j\)-Schleife
- \(1\) Vergleich
Gesamtanzahl der Operationen

\[ \sum_{j=0}^{n-1} 1 = n \]

Aufwand \(\mathcal{O}(n)\) im worst case

def search(vector, target):
    for i in range(len(vector)):
        if vector[i] == target:
            return i
    return -1

Binäre Suche im sortierten Vektor#

Voraussetzung: Vektor ist aufsteigend sortiert
Modifiziere Idee des Bisektionsverfahrens
- d.h. natürliche Suche im Telefonbuch
- Betrachte halben Vektor, falls \( vector[j]\neq value\)
Frage: Wieviele Iterationen hat der Algorithmus?
- jeder Schritt halbiert Vektor
- Falls \(n\) Zweierpotenz, gilt \(n/2^k = 1\)
- dann maximal \(1 + \log_2 n\) Schritte
- in jedem Schritt: 2 Vergl. + 2 Zuw. + 1 Division + 3 Add./Subtr.
Aufwand \(\mathcal{O}(\log_2n)\), d.h. logarithmischer Aufwand
- sog. sublinearer Aufwand \(\mathcal{O}(\log_2n) \ll \mathcal{O}(n)\)

def binsearch(vector, target):
    low = 0
    high = len(vector) - 1
    while low <= high:
        mid = (low + high) // 2
        if vector[mid] == target:
            return mid
        elif vector[mid] < target:
            low = mid + 1
        else:
            high = mid - 1
    return -1

Minsort#

In jedem Schritt der \(i\)-Schleife
- \(1\) Zuweisung
- \(j\)-Schleife von \(i+1\) bis \(n-1\)
  - \(1\) Vergleich
  - ggf. \(1\) Zuweisung (worst case!)
  - Vertauschung: 3 Zuweisungen (Dreieckstausch)
quadratischer Aufwand \(\mathcal{O}(n^2)\), weil:

\[ \sum_{i=0}^{n-1} \Big(1 + \sum_{j=i+1}^{n-1}5\Big) = n-1+\sum_{i=0}^{n-1}5\big(n-(i+1)\big) = n-1+5\sum_{i=1}^{n}i = n-1+5\,\frac{n(n-1)}2 \]

def minsort(vector):
    for i in range(len(vector)):
        # Find the minimum element in the unsorted portion of the array
        min_idx = i
        for j in range(i+1, len(vector)):
            if vector[j] < vector[min_idx]:
                min_idx = j
        # Swap the found minimum element with the first element of the unsorted portion
        vector[i], vector[min_idx] = vector[min_idx], vector[i]

Aufwand & Rechenzeit#

Jede Operation kostet Rechenzeit
- d.h. Aufwand korrespondiert zu Rechenzeit
Frage: Welche Rechenzeit kann ich erwarten?
- Antwort kann nur eine relative Größe sein, da Rechner unterschiedlich schnell
theoretische Voraussagen
- linearer Aufwand
  - Problemgröße \(n\) \(\rightarrow\) \(Cn\) Operationen
  - Problemgröße \(kn\) \(\rightarrow\) \(Ckn\) Operationen
  - d.h. \(3\times\) Problemgröße \(\rightarrow\) \(3\times\) Rechenzeit
- quadratischer Aufwand
  - Problemgröße \(n\) \(\rightarrow\) \(Cn^2\) Operationen
  - Problemgröße \(kn\) \(\rightarrow\) \(Ck^2n^2\) Operationen
  - d.h. \(3\times\) Problemgröße \(\rightarrow\) \(9\times\) Rechenzeit
- etc.
BSP. Code braucht \(1\) Sekunde für \(n=1000\)
- Aufwand \(\mathcal{O}(n)\) \(\rightarrow\) \(10\) Sekunden für \(n=10000\)
- Aufwand \(\mathcal{O}(n^2)\) \(\rightarrow\) \(100\) Sekunden für \(n=10000\)
- Aufwand \(\mathcal{O}(n^3)\) \(\rightarrow\) \(1000\) Sek. für \(n=10000\)

Zeitmessung#

Wozu Zeitmessung?
- Vergleich von Algorithmen / Implementierungen
- Überprüfen theoretischer Voraussagen
Modul time
- time.time() liefert aktuelle Zeit in Sekunden seit 1.1.1970
- start = time.time() vor Code
- end = time.time() nach Code

Beispiel: Zeitmessung#

Um Aufwand zu vergleichen macht es Sinn die Zeit für große \(n\) zu messen
Zum Beispiel \(n=2^k\) für \(k=1,2,\ldots\)

import time
N = 14

for n in range(N):
  m = 2**n
  sorted_vec = list(range(m))
  unsorted_vec = sorted_vec[::-1]

  # Measure time for search
  start = time.time()
  search(sorted_vec, m-2)
  end = time.time()
  time_search = end - start
  # Measure time for binsearch
  start = time.time()
  binsearch(sorted_vec, m-2)
  end = time.time()
  time_binsearch = end - start
  # Measure time for minsort
  start = time.time()
  minsort(unsorted_vec)
  end = time.time()
  time_minsort = end - start

  print(f"n={m:8d} search={time_search:.6f}s binsearch={time_binsearch:.6f}s minsort={time_minsort:.6f}s")

n=       1 search=0.000001s binsearch=0.000002s minsort=0.000002s
n=       2 search=0.000001s binsearch=0.000001s minsort=0.000002s
n=       4 search=0.000001s binsearch=0.000001s minsort=0.000003s
n=       8 search=0.000001s binsearch=0.000001s minsort=0.000006s
n=      16 search=0.000002s binsearch=0.000001s minsort=0.000014s
n=      32 search=0.000002s binsearch=0.000002s minsort=0.000042s
n=      64 search=0.000003s binsearch=0.000002s minsort=0.000167s
n=     128 search=0.000005s binsearch=0.000001s minsort=0.000274s
n=     256 search=0.000006s binsearch=0.000001s minsort=0.001005s
n=     512 search=0.000012s binsearch=0.000002s minsort=0.004120s
n=    1024 search=0.000307s binsearch=0.000004s minsort=0.030188s
n=    2048 search=0.000051s binsearch=0.000002s minsort=0.095638s
n=    4096 search=0.000097s binsearch=0.000003s minsort=0.320854s
n=    8192 search=0.000416s binsearch=0.000005s minsort=1.165473s

quadratischer Aufwand ist deutlich teurer als linearer Aufwand

Minsort braucht

ca. 1 Sekunde für \(n= 2^{13}= 8192\)
ca. 4 Sekunden für \(n= 2^{14}= 16384\)
ca. 4.5 Stunden für \(n= 2^{20}= 1048576\)
ca 34 Jahre für \(n = 2^{27}= 134217728\)

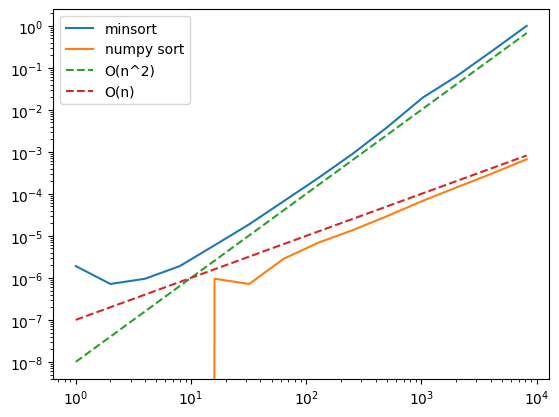
Beispiel: Aufwand plotten#

Um den Aufwand von Algorithmen zu visualisieren eigenen sich logarithmische Plots besonders gut.

der Exponent des Aufwands (linear =1, quadratisch=2, kubisch=3) ist als Steigung der Linie erkennbar

import time
import random as rnd
import matplotlib.pyplot as plt

def minsort(arr):
    n = len(arr)
    for i in range(n):
        min_index = i
        for j in range(i + 1, n):
            if arr[j] < arr[min_index]:
                min_index = j
        arr[i], arr[min_index] = arr[min_index], arr[i]

N = 14
times1 = []
times2 = []
for n in range(N):
    m = 2**n
    data = [rnd.random() for _ in range(m)]
    start = time.time()
    minsort(data)
    end = time.time()
    times1.append(end - start)

    data = [rnd.random() for _ in range(m)]
    start = time.time()
    data.sort()
    end = time.time()
    times2.append(end - start)

xdata = [2**i for i in range(N)]
plt.loglog(xdata, times1, label='minsort')
plt.loglog(xdata, times2, label='numpy sort')
plt.loglog(xdata, [1e-8*x**2 for x in xdata], label='O(n^2)', linestyle='dashed')
plt.loglog(xdata, [1e-7*x for x in xdata], label='O(n)', linestyle='dashed')
plt.legend()
plt.show()

_images/dd6796bb4bfd0b5ba209e6c90663c5eb1cbc35404dd26785bea2348dd7c32e12.png

Aufwand von vorimplementierten Funktionen#

Python liefert viele vorimplementierte Funktionen deren Aufwand nicht immer offensichtlich ist.

Um den Aufwand abzuschätzen, ist es oft hilfreich, sich vorzustellen wie die Funktion implementiert sein könnte.

Beispiel: Listenfunktionen#

Die Funktion list.append(x) hat z.B. im Durchschnitt einen Aufwand von \(\mathcal{O}(1)\), im worst case \(\mathcal{O}(n)\), wenn die Liste vergrößert werden muss.

Python reserviert automatisch mehr Speicher als benötigt, um im Fall von Erweiterungen nicht jedes Mal den gesamten Speicher neu zuordnen zu müssen.
Wenn dieser zusätzliche Speicher nicht mehr ausreicht, wird eine neue, größere Speicherstelle zugewiesen und der gesamte Inhalt der Liste dorthin kopiert. Dies verursacht den worst-case Aufwand von \(\mathcal{O}(n)\).

import time
x = [0]
n = 10**7
max_time = 0 
mean_time = 0
for i in range(n):
    start = time.time()
    x.append(0)
    end = time.time()
    max_time = max(max_time, end-start)
    mean_time += (end-start)
mean_time /= n
print("Mittelwert Zeit für append:", mean_time)
print("Max Zeit für append:", max_time)

Mittelwert Zeit für append: 7.821056842803956e-08
Max Zeit für append: 0.011293172836303711

Die Funktion list.insert(i, x) hat im worst case einen Aufwand von \(\mathcal{O}(n)\), da alle Elemente ab Index i um eine Position verschoben werden müssen.

n = 10**5
x = [0]*n
start = time.time()
x.insert(0, 1)
end = time.time()
print("Zeit für Einfügen am Anfang:", end-start)

Zeit für Einfügen am Anfang: 0.00012731552124023438

Das Erstellen einer Liste mit list(range(n)) oder x = [0]*n hat einen Aufwand von \(\mathcal{O}(n)\), da n Elemente erstellt und in die Liste eingefügt werden müssen.

n = 10**7
start = time.time()
x = [0]*n
end = time.time()
print("Zeit für Erstellen Liste der Länge n:", end-start)

Zeit für Erstellen Liste der Länge n: 0.006880283355712891

Beispiel: Matrix-Vektor Multiplikation#

Aufwand \(\mathcal{O}(n)\) für das Anlegen des Ergebnisvektors in Zeile 2
Schleife von 1 bis n in Zeile 3
- Schleife von 1 bis n in Zeile 4
  - 1 Multiplikation und 1 Addition in Zeile 5
Aufwand für die Schleifen also

\[ \sum_{j=0}^{n-1} \sum_{k=0}^{n-1} 2 = \sum_{j=0}^{n-1} 2n = 2n^2 \]

Insgesamt also Aufwand \(\mathcal{O}(n) + \mathcal{O}(n^2) = \mathcal{O}(n^2)\)

def matrix_vector_mult(A, x, n):
    y = [0]*n # Ergebnisvektor  initialisieren
    for j in range(n):
        for k in range(n):
            y[j] += A[j][k] * x[k]
    return y

Aufwand: Zusammenfassung#

Quadratischer Aufwand für große \(n\) spürbar
Fazit: Algorithmen sollen kleinen Aufwand haben
- Ziel der numerischen Mathematik
- nicht immer möglich, oft offene Frage, z.B., Aufwand für Lösen von LGS, oder \({\rm P}\neq {\rm NP}\) in der Informatik